2.a La distribuzione di Boltzmann

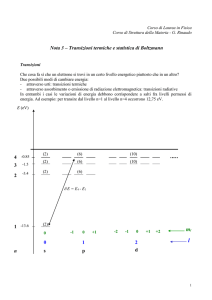
La distribuzione di Boltzmann
2.a La distribuzione di Boltzmann
Ludwig Eduard Boltzmann
Austria 1844 – 1906
Josiah Willard Gibbs
USA 1839 – 1903
2.a La distribuzione di Boltzmann
Un sistema fisico costituito da N particelle ha 6N gradi di libertà:
N vettori posizione
N vettori velocità
→
→
3N componenti scalari
3N componenti scalari
Se il sistema è macroscopico, N ≈ 1023
E’ concettualmente impossibile valutare così tanti parametri.
La descrizione di un sistema macroscopico passa sempre per la
definizione di alcuni parametri, detti funzioni (termodinamiche) di stato.
Esempio di funzioni di stato:
temperatura T, volume V, pressione P. densità ρ, magnetizzazione M,
polarizzazione dielettrica P, massa m, energia interna E, ecc.
Le funzioni estensive raddoppiano se si duplica il sistema:
(numero di particelle, massa, Energia interna…)
Le funzioni intensive non cambiano se si duplica il sistema:
(densità, pressione…)
2.a La distribuzione di Boltzmann
I microstati
Un microstato è fissato dalla (ipotetica) conoscenza di 6N parametri microscopici, almeno entro un errore
prefissato:
qi ≤ xi ≤ qi + ε
w i ≤ v i ≤ w i + ε'
xi = una delle coordinate di una delle particelle
vi = una delle componenti della velocità di una delle particelle
I macrostati
Un macrostato è fissato dalla (reale) conoscenza delle funzioni termodinamiche di stato:
V ≤ V ≤ V +∆V
P ≤ P ≤ P + ∆P
...
Il numero di microstati corrispondenti a un certo macrostato è indicato dal simbolo Ω:
Un macrostato (T, P, V , …)
→
Ω diversi microstati
2.a La distribuzione di Boltzmann
I sistemi isolati
Un sistema isolato non può scambiare né energia né materia con l’ambiente esterno.
Fissato il macrostato, le particelle di un sistema isolato passano continuamente da un microstato all’altro.
Nelle condizioni usuali si assume che ciascun microstato sia visitato con uguale frequenza (Teorema di Liouville).
t1
t2
( T, P, V… )
I Microstati di un sistema isolato sono equiprobabili
t3
2.a La distribuzione di Boltzmann
L’Entropia di Boltzmann-Gibbs
All’equilibrio termodinamico, un sistema isolato si porta nel macrostato più probabile, cioè quello che conta più
microstati
Macrostato 1: Atomi blu a sinistra, grigi a destra
Macrostato 2: Atomi mescolati
Al macrostato 2 corrispondono più microstati che al macrostato 1
2.a La distribuzione di Boltzmann
L’Entropia di Boltzmann-Gibbs
Ω:
Numero di Microstati corrispondenti allo stesso Macrostato
Formula di Boltzmann - Gibbs
S = kB ln Ω
S
Ω
kB
Entropia
Numero di microstati
Costante di Boltzmann
Al Macrostato più probabile corrisponde la massima entropia
All’equilibrio termodinamico, un sistema isolato si trova nel macrostato con entropia più alta
2.a La distribuzione di Boltzmann
p
La costante di Boltzmann
kB = 1.3 × 10-23 J K-1
kB = 8.6 × 10-5 eV K-1
V
Nella legge dei gas perfetti:
P V = N kB T
N = nA
⇔
A = 6 × 10 23 mol −1
;
R = A k B = 8.3
PV = nRT
J
mol K
2.a La distribuzione di Boltzmann
I sistemi interagenti con un reservoir a temperatura T
Un sistema a contatto con un bagno termico (reservoir) può scambiare energia (sotto forma di calore).
In queste condizioni, i microstati non sono più equiprobabili.
La probabilità di un microstato dipende dall’energia interna del macrostato cui appartiene.
Macrostato con energia interna E fissata
Ω(E) : Numero di microstati nel macrostato di energia E
E1
E2
E5
E3
E4
Insieme di tutti i macrostati possibili (ensamble canonico)
2.a La distribuzione di Boltzmann
I sistemi interagenti con un reservoir a temperatura T
Quando un sistema può scambiare energia con reservoir a temperatura T, la probabilità che esso si
trovi in un Macrostato di energia interna E è data dalla funzione di distribuzione di Boltzmann:
−
p (E ) =
E:
Ω(E) :
Z:
Ω (E ) e
E
kB T
Z
Somma di tutte le energie cinetiche e potenziali della particelle del sistema
Numero di Microstati corrispondenti all’energia interna E
“Funzione di partizione”. E’ in pratica una costante di normalizzazione.
Fattore di normalizzazione
p (E ) =
Probabilità di un microstato
1
Z
−
Ω (E )
e
E
kB T
Numero dei microstati
2.a La distribuzione di Boltzmann
Confronto tra l’equilibrio dei sistemi isolati e dei sistemi in contatto con un reservoir
Fattore di normalizzazione
Sistema isolato
Tutti i microstati hanno la stessa energia e sono equiprobabili
p =
Il macrostato più probabile è quello di massima entropia.
Ω
Numero dei microstati
Probabilità di un microstato
Fattore di normalizzazione
p (E ) =
1
Z
1
Z
−
Ω (E )
e
E
kB T
Numero dei microstati
Sistema in contatto con un reservoir
I microstati con energia E più bassa hanno probabilità più alta,
ma i microstati con energia più alta sono di più!
Il macrostato più probabile nasce da un compromesso tra minima
energia e massima entropia.
2.a La distribuzione di Boltzmann
−
f = e
La funzione
E
kB T
f (E )
Grafico di f in funzione di E, con T = To = cost
Si confrontano le probabilità di macrostati di diversa
energia interna, a temperatura bloccata.
Lo stato di energia più bassa è più probabile.
1.0
To = cost
0.5
0.0
0
f (T )
1
0.8
Eo = cost
2
3
E
k B To
0.6
Grafico di f(T), con E = Eo = cost
0.4
Si confrontano le probabilità dello stesso macrostato,
al variare della temperatura.
La probabilità cresce all’aumentare della temperatura.
0.2
0.0
0
1
2
3
kB T
Eo
2.b La distribuzione di Boltzmann
I sistemi termodinamici e la distribuzione di Boltzmann
Un sistema macroscopico che possa essere descritto da un
insieme di funzioni di stato è detto sistema termodinamico.
Particelle indistinguibili
Una singola particella può essere trattata come un sistema termodinamico?
Dipende.
Se la particella è isolata, può essere riconosciuta individualmente e trattata come un sistema
termodinamico.
Esempio: l’elettrone di un atomo di Idrogeno.
Se invece la particella appartiene a un sistema di particelle identiche, è impossibile riconoscerla
individualmente. Il sistema termodinamico è dunque l’insieme di tutte le particelle.
Esempio: un elettrone di un metallo.
La funzione di distribuzione di Boltzmann è corretta per tutti e soli i sistemi termodinamici. E’ corretta per
descrivere tutto l’insieme di elettroni di un metallo, ma non è adatta a descrivere un singolo elettrone.
2.b La distribuzione di Boltzmann.
Esercizi e complementi.
Entropia e disordine
L’entropia di Boltzmann-Gibbs S = kB ln Ω è una misura del “disordine” dello stato del sistema
Ordine
Macrostato: “In alto i libri verdi; in basso a destra rossi, a sinistra blu”
Numero di Microstati: Ω = 1
Entropia:
S=0
Sistema ordinato: appena sposto un libro, cambio il Macrostato
ordine
Disordine
Macrostato: “In alto alcuni libri verdi e rossi; in basso rossi, verdi e blu”
Numero di Microstati: Ω >> 1
Entropia:
S >> KB
Sistema disordinato: se sposto qualche libro, non cambio il Macrostato
disordine
2.b La distribuzione di Boltzmann.
Esercizi e complementi.
Entropia e Macrostato di equilibrio
Se il sistema non può interagire in nessun modo con l’ambiente esterno, il Macrostato di
equilibrio termodinamico che si realizzerà all’equilibrio termodinamico è quello che conta più
Microstati, perché è più probabile.
Supponiamo ad esempio di saper distinguere solo due
Macrostati: “ordine” e “disordine”.
Qualunque sia lo stato iniziale, il sistema finisce sempre nello
stato “disordine”, che è anche lo stato di equilibrio
termodinamico.
Il disordine è lo stato più probabile:
1
1
p ordine =
≈
<< 1
N +1
N
p disordine =
N
N
≈
= 1
N +1
N
Per raggiungere il disordine basta spostare un libro a caso.
Molto difficile invece tornare all’ordine spostando libri a caso!
I sistemi isolati evolvono verso il macrostato di massima entropia, perché questo è il
macrostato più probabile.
2.b La distribuzione di Boltzmann.
Esercizi e complementi.
La funzione Ω(E)
Nei sistemi più semplici, il numero di Microstati disponibili è una funzione crescente dell’energia
interna E.
207
Per esempio, per un gas perfetto costituito da N
molecole:
 E 

Ω (E ) ∝ 
E
 o 
Ω
4x10
N = 100
207
3x10
αN
;
La funzione ha una crescita violenta.
Nel grafico, N = 100;
nei sistemi macroscopici, N ≈ 1023
α ≈ 1
207
2x10
207
1x10
0
0
50
Qualitativamente, la formula resta vera anche per i sistemi di particelle interagenti.
Ciò garantisce che l’entropia S sia una funzione di stato estensiva:
 E 
 + So
S = kB ln(Ω ) = α N ln 
⇒
S − So ∝ N
E
 o 
La costante di proporzionalità si trasforma in
costante additiva quando si applica il logaritmo
100
E
Eo
2.b La distribuzione di Boltzmann.
Esercizi e complementi.
Il macrostato più probabile per un sistema in contatto con un reservoir
La funzione Ω(E) è fortemente crescente, la funzione f(E) fortemente decrescente.
Il loro prodotto presenta un massimo, che identifica il macrostato più probabile.
Attenzione: i grafici sono in scala logaritmica
f(E)
Ω(E)
Ω(E) f(E)
E
Sistema in contatto con un reservoir
I microstati con energia E più bassa hanno probabilità più alta,
ma i microstati con energia più alta sono di più!
Il macrostato più probabile nasce da un compromesso tra minima energia e massima entropia.
E
2.b La distribuzione di Boltzmann.
Esercizi e complementi.
Entropia e informazione
L’entropia di Boltzmann-Gibbs S = kB ln Ω è una misura dell’ “informazione” dello stato del sistema
Macrostato: “In alto alcuni libri verdi e rossi; in basso rossi, verdi e blu”
Numero di Microstati:
Ω
Elenco dei Microstati:
{ “1”, “2”, … “Ω” }
Numero di cifre decimali necessarie per contare da 1 a Ω:
log10 (Ω )
Numero di bit necessari per contare da 1 a Ω:
log 2 (Ω ) =
S
k B ln 2
A parte un fattore moltiplicativo, l’entropia di Boltzmann-Gibbs
dice quanti bit servono per identificare un certo specifico
Microstato, se sappiamo a che Macrostato appartiene.
Se identifichiamo un Microstato che richiede molti bit, abbiamo ottenuto
molta informazione. Per esempio, riceviamo molta informazione se da una
foto dello scaffale disordinato ricaviamo l’esatta disposizione dei libri. Al
contrario, riceviamo poca informazione dalla foto dello scaffale ordinato:
sapevamo già dove trovare i libri verdi, ecc., prima di fare la foto!
disordine
2.b La distribuzione di Boltzmann.
Esercizi e complementi.
Funzione di Boltzmann
Esercizio
L’elettrone dell’atomo di Idrogeno ha energia meccanica Eo = -13.6 eV nello stato fondamentale e E1 = -3.4 eV
nel primo eccitato.
Determinare che probabilità c’è di trovare un elettrone nel primo eccitato a T = 300 K.
Determinare a che temperatura si deve portare il gas perché la ionizzazione abbia probabilità p = 10-10
2.b La distribuzione di Boltzmann.
Esercizi e complementi.
Energia e stati permessi all’oscillatore quantistico
Gli stati disponibili a un oscillatore quantistico sono individuati dal numero quantico n.
n è un numero naturale:
n ∈ {0,1,… m,…}
A ciascun valore di n corrisponde un solo microstato
possibile, di energia meccanica En:
1 
E n = h ωo  n +

2 

In MQ, il numero di microstati corrispondenti a un dato valore di energia è detto degenerazione.
Gli stati dell’oscillatore armonico hanno degenerazione pari a 1; in altri termini,
Ω ( En ) = 1
∀ n
2.b La distribuzione di Boltzmann.
Esercizi e complementi.
Funzione di Boltzmann
Esercizio
Un oscillatore armonico ha pulsazione h ωo = 40 meV
Determinare con che probabilità l’oscillatore occuperà il primo stato eccitato alla temperatura T = 10 K.
Determinare a che temperatura la probabilità di occupare il livello n = 1 è pari alla metà di quella di occupare lo
stato fondamentale.
2.b La distribuzione di Boltzmann.
Esercizi e complementi.
Funzione di Boltzmann
Per la soluzione degli integrali:
Effettuare la sostituzoine di variabili x =
E
kB T
Ricorrere al calcolatore di integrali Wolfram (su internet)
Esercizio
Calcolare l’energia media di un oscillatore armonico classico di pulsazione ωo alla temperatura T
L’energia media è il valore atteso di E con la funzione di distribuzione di Boltzmann. Nel caso dell’oscillatore
classico, E è una variabile aleatoria continua, con E ∈ [ 0 , ∞ ].
E
∞
=
E
∫
E p (E ) dE
−
1
Ω (E ) e k B T
p (E ) =
Z
;
0
Per un oscillatore armonico, Ω(E) = Ω = cost. Accetteremo questo risultato: la dimostrazione è complicata.
La costante di normalizzazione si ottiene imponendo che l’integrale di p(E) sia pari a 1:
Ω
Z
∞
∫
−
e
−
E
kB T
Z
0
∞
E
Ω
⇒
dE = 1
=
∫
0
∞
E p (E ) dE =
∫
0
E
kB T
−
e
E
kB T
kB T = 1
⇒
dE = k B T
L’energia media dell’oscillatore classico non dipende da ωo.
Ω
Z
=
1
kB T
⇒
p (E ) =
E
kB T
e
kB T
2.b La distribuzione di Boltzmann.
Esercizi e complementi.
Per il calcolo delle somme:
 E 

Effettuare la sostituzione di variabili x = exp 

k
T
 B 
Funzione di Boltzmann
Ricordare le formule per sommare le serie geometriche
Esercizio
Calcolare l’energia media di un oscillatore armonico quantistico di pulsazione ωo alla temperatura T
L’energia media è il valore atteso di E con la funzione di distribuzione di Boltzmann. Nel caso dell’oscillatore
quantistico, E è una variabile aleatoria discreta e può assumere i valori:
1 
E n = h ωo  n +

2 

n = 0, 1, ...
Per ogni n c’è un solo microstato, quindi Ωn = 1. La distribuzione di Boltzmann quindi si scrive:
En
pn
1 − kB T
e
=
Z
La costante di normalizzazione si ottiene imponendo che la somma su n di pn sia uguale a 1:
1
Z
−
∞
∑
e
En
kB T
⇒
= 1
Z =
n=0
∑
∞
=
∑
e
En
kB T
n=0
∞
E
−
∞
∑
n=0
En pn =
En e
E
− n
kB T
n=0
−
∞
∑
e
En
kB T
h ωo
= Eo +
n=0
Questo calcolo valse a Planck il Nobel per la Fisica.
e
h ωo
kB T
+1