7) Termodinamica statistica: energia interna, entropia, calore e

7-1
Termodinamica statistica
Energia interna
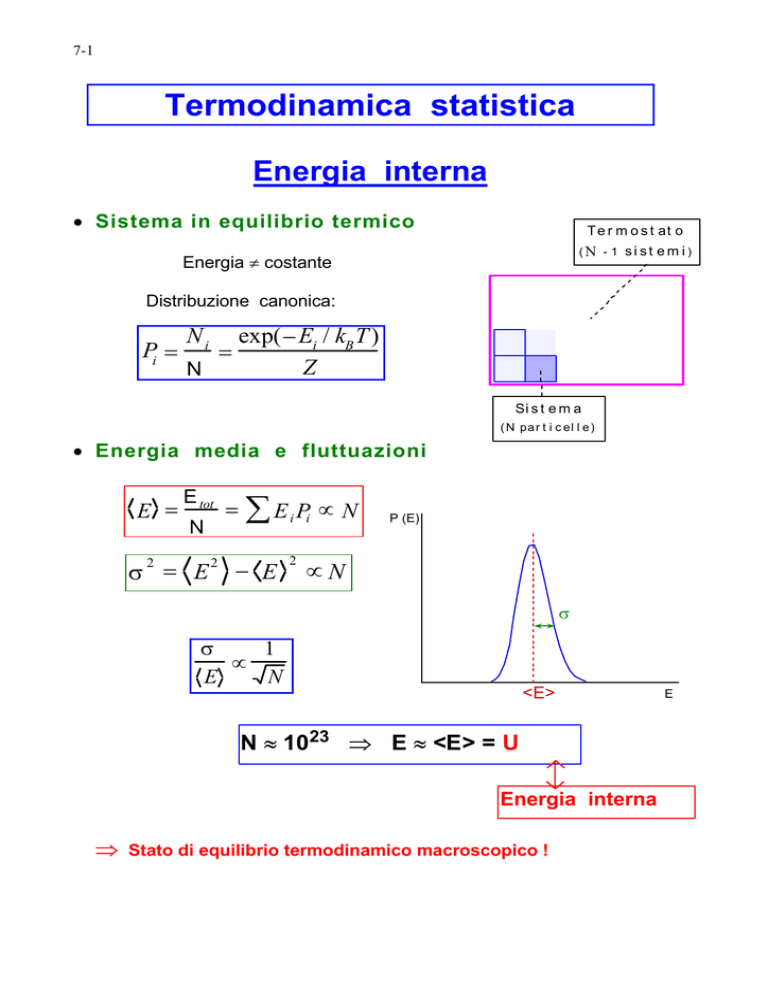
• Sistema in equilibrio termico
T e r m o s t at o
(N - 1 si st em i)
Energia ≠ costante
Distribuzione canonica:
Pi =
Ni
N
=
exp(− Ei / kB T )
Z
Si s t e m a
( N pa r t i c el l e )
• Energia media e fluttuazioni
E =
E tot
N
=
∑E P ∝ N
i i
2
2
σ = E − E
2
P (E)
∝N
σ
1
σ
∝
E
N
<E>
N ≈ 1023 ⇒ E ≈ <E> = U
Energia interna
⇒
Stato di equilibrio termodinamico macroscopico !
E
7-2
Entropia
• Insieme statistico
T e r m o s t at o
N→∞
(N - 1 si s t e m i )
Insieme isolato in equilibrio:
Ωins microstati equiprobabili
Sins = k B ln Ω ins
Ω ins = N !∏
1
Ni!
Si s t e m a
• Entropia del sistema
Sistema non isolato → microstati non equiprobabili
S =
P
Sins
N
=
kB
N
P
i
ln Ω ins =− k B
∑ P ln P
i
P
i
1
2
3
S=0
4
i
i
1
1
1
i
i
1
2
3
4
S = 1.04 KB
1
i
S = 9 KB
Entropia ↔ dispersione rispetto agli stati
2
3
4
i
7-3
• Sistema termodinamico
Ω
1 sistema = 1023 particelle
m i c r os t at i
del
P ( E)
s i s t em a
Concentrazione di micro-stati
Nel picco:
microstati equiprobabili !
Sistema quasi-isolato in equilibrio
<E>
Pi =
1
Ω
S = k B lnΩ
• La prospettiva molecolare
Microstati del sistema:
Ω
=
Ω MB
particelle distinguibili
Ω cl
particelle indistinguibili
(limite classico)
Entropia del sistema:
S = kB ln Ω =
− Nk B ∑ pi ln pi + kB ln N!
− Nk B ∑ pi ln pi
E
7-4
Calore e lavoro
• Termodinamica macroscopica
dU = dQ + dW
= TdS − pdV
•
Termodinamica statistica
E = ∑ Ei Pi
Variazione di
energia interna
E
d E = ∑ Ei dPi + ∑ Pi dEi
=
CALORE
(cambiano le
probabilità)
E
+
LAVORO
(si spostano
i livelli)
E
7-5
•
La prospettiva molecolare
Livelli di energia del sistema ↔ livelli molecolari
E = ∑ ni ε i
d E =
∑ ε dn + ∑ n dε
i
ε
i
i
i
ε
CALORE
(cambiano le
popolazioni)
LAVORO
(si spostano
i livelli)
ε
ε
7-6
Entropia e temperatura
Un esempio: gas ideale monoatomico
•
Lavoro adiabatico
∆U = W
⇒
Q=0
∆U > 0
ε
ε
∆T > 0
∆S = 0
•
Lavoro isotermo
∆U = 0
⇒
W =−Q
∆U = 0
∆T = 0
∆S < 0
ε
7-7
•
Riscaldamento a volume costante
Q = ∆U
⇒
W=0
∆U > 0
ε
∆T > 0
∆S > 0
Temperatura:
dispersione rispetto ai valori dell’energia
Entropia:
dispersione rispetto ai livelli di energia
ε