LA LEZIONE
La funzione di distribuzione delle velocità
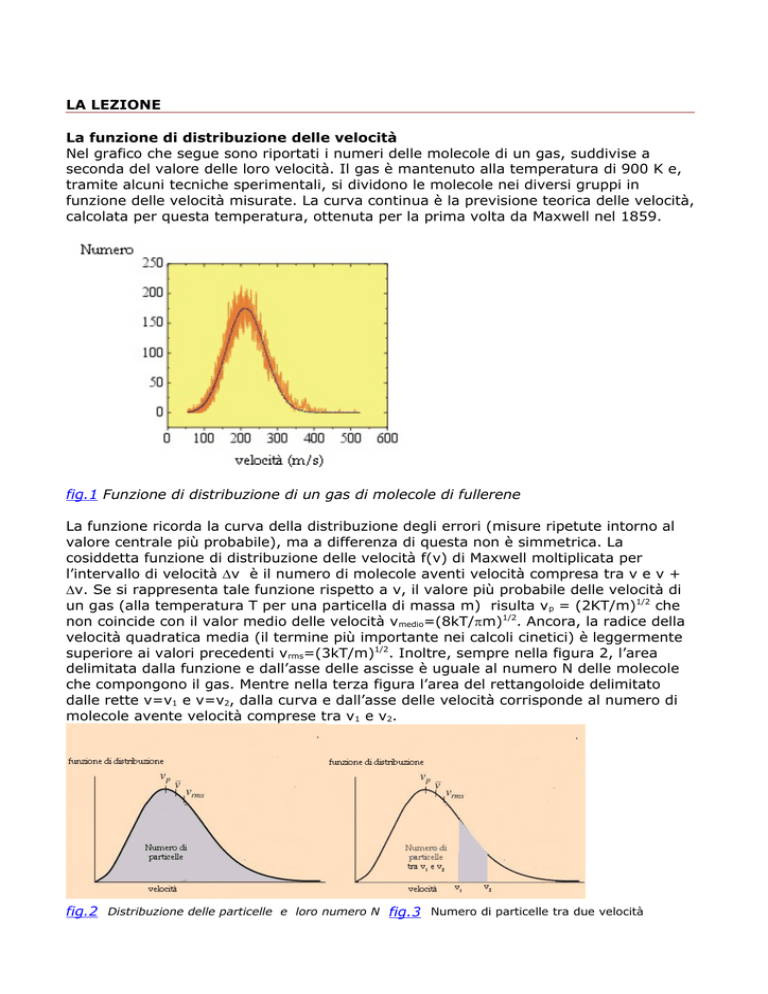
Nel grafico che segue sono riportati i numeri delle molecole di un gas, suddivise a
seconda del valore delle loro velocità. Il gas è mantenuto alla temperatura di 900 K e,
tramite alcuni tecniche sperimentali, si dividono le molecole nei diversi gruppi in
funzione delle velocità misurate. La curva continua è la previsione teorica delle velocità,
calcolata per questa temperatura, ottenuta per la prima volta da Maxwell nel 1859.
fig.1 Funzione di distribuzione di un gas di molecole di fullerene
La funzione ricorda la curva della distribuzione degli errori (misure ripetute intorno al
valore centrale più probabile), ma a differenza di questa non è simmetrica. La
cosiddetta funzione di distribuzione delle velocità f(v) di Maxwell moltiplicata per
l’intervallo di velocità Dv è il numero di molecole aventi velocità compresa tra v e v +
Dv. Se si rappresenta tale funzione rispetto a v, il valore più probabile delle velocità di
un gas (alla temperatura T per una particella di massa m) risulta v p = (2KT/m)1/2 che
non coincide con il valor medio delle velocità vmedio=(8kT/pm)1/2. Ancora, la radice della
velocità quadratica media (il termine più importante nei calcoli cinetici) è leggermente
superiore ai valori precedenti vrms=(3kT/m)1/2. Inoltre, sempre nella figura 2, l’area
delimitata dalla funzione e dall’asse delle ascisse è uguale al numero N delle molecole
che compongono il gas. Mentre nella terza figura l’area del rettangoloide delimitato
dalle rette v=v1 e v=v2, dalla curva e dall’asse delle velocità corrisponde al numero di
molecole avente velocità comprese tra v1 e v2.
fig.2 Distribuzione delle particelle e loro numero N fig.3 Numero di particelle tra due velocità
L’espressione analitica della funzione di distribuzione dipende dalla temperatura
assoluta in modo tale che all’aumentare di T la curva si schiaccia e si allarga (il numero
delle molecole è costante, quindi l’area rimane la stessa).
fig.4 Funzione di distribuzione delle velocità di Maxwell, al variare della temperatura
assoluta
Per basse temperature, i valori sono assai concentrati e possono assumere un ristretto
valore di velocità. La velocità media, o uno degli altri parametri statistici (velocità più
probabile, velocità quadratica media), tende a diminuire. Viceversa, all’aumentare della
temperatura, i valori possibili per le velocità aumentano e il valore massimo ha una
frequenza inferiore ai casi precedenti. Le molecole hanno un ampio spettro di valori.
Tutte le velocità caratteristiche dipendono, come abbiamo detto, dalla radice quadrata
della temperatura misurata in kelvin. Per T tendente a zero, tutte le molecole
“condensano” verso valori prossimi a velocità zero. La temperatura è, per questo
motivo, considerata nei gas una misura dell’agitazione termica. La funzione di
distribuzione delle velocità di un gas all’equilibrio non cambia, pur variando, attraverso
gli urti tra le molecole e le pareti del recipiente, i valori assunti dalla velocità delle
singole molecole. È evidente che, alla base di una simile proprietà, vi siano
considerazioni probabilistiche legate alla tendenza alla regolarità della funzione di
distribuzione dopo un elevatissimo numero di collisioni (o dopo un tempo
sufficientemente lungo).
La nascita della meccanica statistica: la funzione di distribuzione delle energie
di Boltzmann
Con Ludwig Boltzmann l’analisi dell’evoluzione temporale delle N molecole interagenti
del gas è gradualmente sostituita dallo studio delle proprietà statistiche dell’insieme di
molecole. L’apparante inconciliabilità tra la reversibilità della meccanica (per inversioni
temporali) e l’irreversibilità della funzione che descrive l’evoluzione temporale degli urti
di N particelle verso lo stadio di equilibrio, evidenziate da Joseph Loschmidt nel 1876,
trova secondo Boltzmann la seguente spiegazione: non è possibile dimostrare che per
ogni possibile posizione e velocità delle sfere, la loro distribuzione deve diventare più
uniforme dopo un tempo molto lungo; si può solo dimostrare che il numero di stati
iniziali che portano a uno stato uniforme è infinitamente più grande di quello degli stati
iniziali che portano a uno stato non uniforme dopo un intervallo di tempo dato.1
Utilizzando un diverso linguaggio, il numero di microstati corrispondenti allo stato di
equilibrio (caratterizzato dalla distribuzione di velocità uniforme di Maxwell) è
enormemente più grande di quelli che portano ad altre distribuzioni. Nel 1877,
1
Olivier Darrigol, Jürgen Renn, L’Ottocento: la nascita della meccanica statistica,
Storia della scienza 2003
http://www.treccani.it/enciclopedia/l-ottocento-la-nascita-della-meccanica-statistica_(Storia-dellaScienza)/
Boltzmann, con un lavoro sul secondo principio e il calcolo delle probabilità, introduce
una finzione matematica: l’energia di una molecola è considerata multipla di una
quantità finita. In modo da assumere per essa solo valori discreti.
Ne deriva una trattazione combinatoria in cui il numero di molecole N 1, N2, …, Ni,..
aventi le corrispettive energie possibili E1, E 2, …, E i,.. soddisfa i vincoli del numero
complessivo N delle molecole e dell’energia totale E:
N1 + N2 + …+ Ni +..= N
N1 E 1 + N2 E 2+ …+ Ni E i +..= E.
Le probabilità di un macrostato a una data temperatura T diviene così una funzione del
numero Ni di particelle di ogni celletta di energia E i. La ripartizione più probabile è per
Boltzmann quella che massimizza una particolare funzione con i vincoli del numero
totale delle particelle e dell’energia complessiva. La soluzione è una funzione di
distribuzione del numero di particelle Ni dipendente dalle energie Ei nella forma
esponenziale: Ni =a e - Ei /kT con k costante di Boltzmann e a costante da determinare in
base ai vincoli. Oggi la stessa trattazione è effettuata in cellette nello spazio delle fasi
(e del resto lo stesso Boltzmann nel suo articolo passa dalle energie allo spazio delle
velocità). Le cellette hanno inoltre dimensioni finite legate al principio di
indeterminazione che postula l’impossibilità di misurare contemporaneamente ed
esattamente la componente p della quantità di moto di una particella e la
corrispondente componente q della posizione. Le energie degli stati possibili molecolari
possono assumere solo valori discreti: E0, E1, E 2, …, E i, e, all’equilibrio termico, la
probabilità di avere una molecola nello stato di energia Ei è proporzionale alla funzione:
e - Ei /kT.
Entropia e probabilità
Consideriamo il solito gas perfetto monoatomico contenuto in un recipiente A avente
pareti rigide e conduttrici, immerso in un bagno termico. Tramite una valvola esso è
collegato a un recipiente B, identico ad A, inizialmente vuoto. Aprendo la valvola il gas
diffonde e, aspettando un tempo sufficientemente lungo, la densità è uniforme nei due
recipienti. Il termometro nel bagno termico non registra variazioni di temperatura. La
trasformazione è isoterma quindi l’energia interna del gas non può essere variata. Cosa
si può dire dell’entropia?
fig.5 Diffusione isoterma di un gas
Se essa dipendesse solo dall’energia non subirebbe variazioni. Invece, come abbiamo
ripetuto più volte, in una trasformazione irreversibile senza scambi con l’ambiente
l’entropia aumenta. La grandezza estensiva che cambia nella diffusione del gas è il
volume che passa dal valore
Vi = VA a Vf = VA+ VB=2 VA,
quindi è probabile che l’entropia sia una funzione del volume. In effetti la formula
dell’entropia di un gas perfetto monoatomico, non considerando la dipendenza dalla
temperatura, assume la forma S = R ln V + costante (con R costante dei gas). Dunque
la variazione di entropia nella trasformazione isoterma risulta
DS = R ln 2VA- R ln VA= R ln (2VA/VA) = R ln 2.
Andiamo a visualizzare la situazione dal punto di vista microscopico. Le sferette sono
gli atomi di gas. Fra tutte le situazioni possibili, in accordo alle considerazioni di
Boltzmann, il gas evolve fino a raggiungere la densità uniforme nei due recipienti che
corrisponde allo stato più probabile fra tutte le configurazioni possibili. Ma come si può
calcolare la molteplicità delle configurazioni corrispondenti al particolare macrostato?
La situazione iniziale (la possibilità che il gas rimanga solo nel recipiente A) è quella
meno probabile.
fig.6 Diffusione isoterma di un gas: interpretazione microscopica. Il macrostato con più
bassa probabilità
Si dice, in questo caso, che essa ha molteplicità 1 (vedremo tra poco come si valuta la
molteplicità). Tutte le particelle sono in un solo recipiente. Diciamo anche che la sua
entropia vale zero. La configurazione più probabile è invece quella in cui metà degli
atomi si trova nel primo e l’altra metà nel secondo volume. Il valore dell’entropia è, per
le considerazioni precedenti, R ln 2.
fig.7 Diffusione isoterma di un gas: interpretazione microscopica. Il macrostato con più
alta probabilità
Per capire il modo di contare la molteplicità dei microstati iniziamo con una situazione
molto diversa dal gas. Due urne A e B con una sola pallina numerata. I casi possibili
sono solo 2 (la pallina è in A oppure in B). Con due palline i casi diventano 4. Con 3
otto e così via.
fig.8 Distribuzione di tre sferette in due recipienti: molteplicità dei microstati
corrispondenti
Con N particelle abbiamo perciò 2N possibilità. Accettiamo per l’entropia l’espressione di
Planck-Boltzmann S = k ln W, con W numero di microstati equivalenti (molteplicità)
che corrispondono allo stato più probabile. Dobbiamo ancora, nel nostro caso, togliere
a 2N i casi meno probabili rispetto alla distribuzione uniforme. Ma le considerazioni sul
numero trascurabile delle situazioni di non equilibrio rispetto a quelle di equilibrio (per
il grande valore di N) ci permettono di approssimare nel nostro caso W finale=2N e
Winiziale=1. Da cui:
DS = k ln Wfinale=k ln 2N - 0 = kN ln 2.
Ricordando infine che il gas è monoatomico, N è uguale al numero di Avogadro, e si
può infine scrivere per la variazione di entropia dell’espansione isoterma dei gas
DS = R ln 2.2
2
L'unico testo liceale che prova a ricavare S=klnW è il testo di Battimeli, Stilli. Le ipotesi a loro necessarie,
tra cui l’approssimazione di Stirling e il calcolo combinatorio, sono sviluppate in diverse unità didattiche












