Corsi di Laurea in Ingegneria
Prova scritta di Fisica Generale 1 (Prof. G. Naletto)
Corsi estivi a Bressanone - Bressanone, 10 Agosto 2012
Cognome .............................................................. Nome ........................................... Matricola .......................
Docente di riferimento a Padova: Prof. ...................................................................
Problema 1
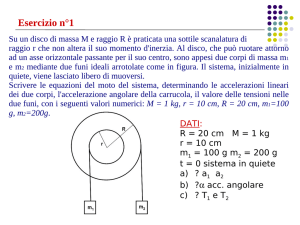
Un corpo di dimensioni trascurabili e massa m = 0.9 kg viene messo in moto
con
velocità iniziale di modulo vo formante un angolo θ = 50° rispetto al
vo
piano orizzontale (verso l’alto, vedi figura). Dopo un tempo tm = 2 s esso
raggiunge il punto A di massima altezza h rispetto al piano orizzontale di
B
θ
partenza. In questo istante, il corpo entra in contatto con la parte concava di
una guida liscia AB posta nel piano verticale in cui avviene il moto del corpo:
la guida è un settore circolare di raggio di curvatura R = h/2 e lunghezza πR/2,
il punto A della guida è tangente alla traiettoria del punto nel punto di contatto, ed il punto B è più basso di A (vedi
figura). Determinare:
a) la massima altezza h raggiunta dal corpo;
b) il modulo aB dell’accelerazione del corpo un istante prima di uscire dalla guida circolare in B.
A
R
Problema 2
Un corpo puntiforme A di massa mA = 4 kg giace su un piano orizzontale liscio. Il
corpo è collegato da un lato ad una molla orizzontale di costante elastica k = 1200
N/m vincolata all’altro estremo; dal lato opposto il corpo è collegato ad una fune
inestensibile di massa trascurabile alla cui altra estremità si trova il corpo B di
massa mB = 2.5 kg soggetto alla forza peso, per mezzo di una carrucola ideale. Il
B
sistema è inizialmente mantenuto fermo dall’azione di una forza verticale orientata
verso il basso applicata in B di modulo F = 80 N. Ad un certo istante si rimuove la
F
forza F ed il sistema inizia a muoversi. Determinare:
a) l’allungamento ∆x della molla quando è applicata la forza F su B;
b) l’accelerazione a (modulo, direzione e verso) di B nell’istante in cui, dopo aver rimosso la forza F, la lunghezza della
molla è pari alla lunghezza a riposo.
A
Problema 3
A
vA
B
AB
v’
vB
P
Due sbarrette omogenee sottili identiche A e B di lunghezza l = 0.6 m e massa
m = 3.5 kg possono scorrere senza attrito su un piano orizzontale. Le due
sbarrette sono parallele e tali che un estremo della sbarretta B stia sull’asse
della sbarretta A. La sbarretta B ha velocità di modulo vB = v = 0.2 m/s,
perpendicolare alla sbarretta stessa; la sbarretta A, che si trova “dietro” la
sbarretta B relativamente al verso del moto di B, ha velocità di modulo
vA = 2v parallela e concorde a vB. Ad un certo istante le due sbarrette si urtano
in modo completamente anelastico e formano un corpo AB che rototrasla.
Determinare:
a) il modulo ω’ della velocità angolare di AB dopo l’urto (suggerimento: si consideri il centro di massa del sistema AB
come polo per il calcolo del momento angolare);
b) l’energia cinetica Ek,AB del corpo AB.
Nel suo moto, il centro di massa del sistema AB urta contro un piolo fisso sul piano orizzontale, in modo che il
sistema vi rimane attaccato pur continuando a ruotare nel piano. Sapendo che quest’urto è durato ∆t = 0.01 s,
determinare:
c) il modulo RP della reazione vincolare, assunta come costante nel tempo, esercitata dal piolo durante l’urto.
Problema 4
Quattro moli di gas ideale monoatomico contenute in un cilindro adiabatico chiuso da un pistone adiabatico di massa
trascurabile che può muoversi senza attrito si trovano nello stato iniziale A in cui occupano un volume VA. A seguito di
una espansione estremamente lenta, il gas viene portato nello stato B in cui occupa un volume VB = 3VA ed ha la
temperatura TB. A questo punto il gas, posto in contatto termico con un serbatoio ideale alla temperatura TB, esegue una
trasformazione molto lenta fino allo stato C, con VC = VA. Infine, bloccato il pistone e posto il gas in contatto termico con
un serbatoio alla temperatura TA, il gas ritorna allo stato iniziale A variando così la sua energia interna di ∆UCA = 10000 J.
Determinare:
a) il valore TA della temperatura del gas in A;
b) il rendimento η del ciclo.
Problema 5
Una macchina termica di rendimento η = 0.2 lavora tra un serbatoio ideale di calore alla temperatura T2 = 400 K ed una
miscela di acqua e ghiaccio alla temperatura T1 = 273.15 K di fusione del ghiaccio. Il lavoro prodotto dalla macchina
termica viene utilizzato da una macchina frigorifera sincrona di efficienza ξ = 1.3 che lavora tra un serbatoio ideale alla
temperatura To = 250 K ed il serbatoio ideale a temperatura T2. Sapendo che la massa di ghiaccio che fonde in un ciclo
della macchina termica è pari a m = 0.005 kg e ricordando che il calore latente di fusione del ghiaccio è λ = 3.3⋅105 J/kg,
determinare:
a) il lavoro W fatto dalla macchina termica in un ciclo;
b) la variazione ∆SU di entropia dell’universo (inteso come il sistema delle macchine termica e frigorifera e dei relativi
serbatoi) in un ciclo.
Soluzioni
Problema 1
a)
b)
v y ( y = h) = 0 = voy − gtm = vo sin θ − gtm
⇒ vo =
gtm
= 25.6 m/s
sin θ
1
1
1
h = voy t m − gtm2 = vo t m sin θ − gtm2 = gtm2 = 19.6 m
2
2
2
1 2
1
v A = v x = vo cosθ = 16.4 m/s; Em, A = Em,B ⇒
mv A + mgR = mv B2
2
2
2
⇒ aB =
a B2 ,T
+ a B2 ,N
⇒ vB = v 2A + gh = 21.5 m/s
2
v2
2v 2
= g + B = g 2 + A + 2g = 48.2 m/s2
R
h
2
Problema 2
T − k∆x = 0
T 1
a)
⇒ ∆x = = (mB g + F ) = 0.087 m
m
g
+
F
−
T
=
0
k k
B
Si orienta positivamente l’asse orizzontale di A verso destra, e quello verticale di B verso il basso.
T ' = m A a
mB
⇒ m B g − m A a = mB a ⇒ a =
g = 3.77 m/s2
b)
m
g
−
T
'
=
m
a
m A + mB
B
B
L’accelerazione a è orientata verso il basso.
Problema 3
a)
b)
c)
2
1
7
l 7
I AB,CM = 2 m l 2 + m =
m l 2 ; LCM , f = I AB,CM ω ' =
m l 2ω ' ;
12
4
24
24
l
7
6v
LCM ,i = LCM , f ⇒
mv =
m l 2ω ' ⇒ ω ' =
= 0.286 rad/s
4
24
7l
3
P = cost ⇒ m v A + m v B = 2 m v ' ⇒ v ' = v;
2
1
1
1 7
36 v 2 1
9
33
E k , fin = E k '+ E k ,CM = I AB ,CM ω ' 2 + 2 m v ' 2 =
ml 2
+ 2m v 2 =
m v 2 = 0 .33 J
2
2
2 24
4
14
49 l 2 2
r
r
r
r
r
2 m v'
J = RV dt = ∆ P ⇒ RV ∆ t = 0 − 2 m v ' ⇒ RV =
= 210 N
∆t
LCM ,i =
l
l
l
m v A − m v B = m v;
4
4
4
∫
Problema 4
p
A
a)
T AV Aγ −1 = TBVBγ −1
V
⇒ TB = TA A
VB
γ −1
; ∆U CA = ncV (TA − TC ) = ncV (TA − TB ) =
V γ −1
∆U CA
= ncV TA 1 − A ⇒ TA =
= 386 K; ⇒ TB = 185.6 K
V γ −1
VB
ncV 1 − A
VB
C
B
V
b)
W + WBC
W
η=
= AB
=
Q ASS
QCA
− ncV (TB − TA ) + nRTB ln
ncV (TA − TC )
VC
VB
VA
VB
=1+
= 0.322
cV (TA − TB )
RTB ln
Problema 5
Q1
η
mλ
; Q1 = −mλ = −1650 J ⇒ Q2 =
= 2062 J; W = ηQ2 = mλ
= 412 J
Q2
1 −η
1 −η
a)
η = 1+
b)
W F = −W ; ξ =
∆SU = ∆S amb =
Qo
Q
= o
WF
W
⇒
Qo = W ξ = 536 J;
− Q o − Q1 −Q2 − Q2, F
+
+
= 1.11 J/K
To
T1
T2
Q2 ,F = W F − Qo = −W − Qo = −949 J