La rivelazione della grandezza fisica S presuppone

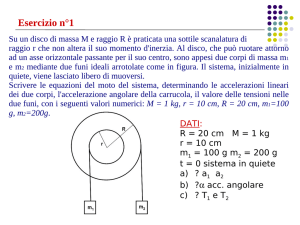
Una sbarretta omogenea di massa m=300 g e lunga L è incernierata, senza
attrito, a un estremo O. Una molla ideale di costante elastica k=110 N/m,
fissata per un estremo al soffitto e per l’altro estremo agganciata alla
sbarretta nel punto P, distante 2L/3 dall’estremo O, mantiene la sbarra
orizzontale in posizione di equilibrio.
1) Sapendo che D=90,0 cm è la distanza fra il soffitto ed il piano
orizzontale passante per O, determinare la lunghezza a riposo della molla.
2) Supponendo di spostare la sbarra dalla posizione di equilibrio
imprimendole, al tempo t=0, la velocità angolare 𝜃(𝑡 = 0) = ̇ −1.55 𝑠 −1
(rotazione oraria) si determini l'equazione del moto ed il periodo delle
piccole oscillazioni verticali della sbarretta.
D
Soluzione
Le forze attive sulla sbarretta sono la forza elastica dovuta alla molla, la forza peso e la reazione del
vincolo in O.
1) Calcolando i momenti delle forze rispetto al punto O l’equilibrio in posizione orizzontale della
sbarretta è garantito dal fatto che si annulla la somma dei momenti della forza peso e della forza
elastica. In tali condizioni la molla è elongata di una quantita’ Δyeq=D-D0 , avendo indicato con D0 la
lunghezza a riposo della molla. Possiamo quindi scrivere L/2 mg = 2/3 L k Δyeq ; da cio’ si ricava
k (D-D0) = ¾ mg
da cui D0= D- 3mg/(4k) = 88,0 cm.
(1)
2) Lasciando la sbarretta libera di muoversi dopo averle fatto subire un piccolo spostamento verticale il
sistema inizia ad oscillare. Tale spostamento comporta un ulteriore allungamento y della molla.
Utilizzando la seconda equazione cardinale della meccanica per i sistemi rigidi possiamo scrivere:
mg L/2 – 2/3 L k (Δyeq + y) = IO dω/dt
dove IO = mL2/3.
Tenendo conto della (1) otteniamo
mg L/2 – 2/3 L ¾ mg - 2/3 L k y = IO dω/dt , cioè
-2/3 L k y = IO dω/dt
(2)
Detto θ l’angolo formato dalla sbarretta con l’orizzontale, per piccole deformazioni verticali della molla
possiamo scrivere y ≈ 2/3 L θ ed ancora ω = dθ / dt.
Sostituendo quindi nella (2) otteniamo -4/9 L2 k θ = mL2/3 d2θ/dt2 e quindi semplificando:
d2θ/dt2 + 4/3 k/m θ = 0.
Il moto della sbarretta sara’ quindi un moto oscillatorio attorno alla posizione orizzontale con
4𝑘
pulsazione ω = √3𝑚 = 22.1 s-1 periodo 𝑇 =
2𝜋
ω
3𝑚
= 2𝜋√ 4𝑘 = 0.284 s.
θ(t) = Acos(ωt + φ).
L'ampiezza di oscillazione A e la fase φ si possono determinare conoscendo posizione e velocità
angolare per t=0:
π
θ(t = 0) = 0 = Acos(φ) da cui φ = 2
θ̇(t = 0) = 0 = −Aωsin(φ) = −1.55 = −Aω da cui A=1.55/22.1=7.0110-2 = 4 gradi
La legge del moto è quindi
4𝑘
θ(t) = 7.01 ∙ 10−2 sin(√3𝑚 t).
Possiamo risolvere il problema anche utilizzando la conservazione della Energia Meccanica, valida nel
caso in esame visto che forza peso e forza elastica costituiscono campi di forze conservativi:
Upeso+Uelastica+K = cost
Definiamo Upeso ed Uelastica rispettivamente l'energia potenziale relativa alla forza peso ed a quella
elastica e K l'energia cinetica. Se assumiamo la quota del c.m. della sbarra orizzontale come
riferimento per l'energia potenziale della forza peso, quando la sbarra forma un generico angolo  con
1
1
2
l'orizzontale (come in figura) abbiamo 𝑈𝑝𝑒𝑠𝑜 = −𝑚𝑔 2 𝐿𝑠𝑖𝑛θ, 𝑈𝑒𝑙𝑎𝑠𝑡𝑖𝑐𝑎 = 2 𝑘(Δ𝑦𝑒𝑞 + 3 𝐿𝑠𝑖𝑛θ)2 .
1
L'energia cinetica di rotazione attorno all'asse orizzontale passante per O e' data da 𝐾 = 2 𝐼𝑜 𝜔2 dove
1
𝐼𝑜 = 3 𝑚𝐿2 e 𝜔 =
𝑑𝜃
𝑑𝑡
meccanica totale si ha:
è la velocità angolare istantanea. Invocando la conservazione dell'energia
𝑑
𝑑𝑡
1
1
2
1
(−𝑚𝑔 2 𝐿𝑠𝑖𝑛θ + 2 𝑘(Δ𝑦𝑒𝑞 + 3 𝐿𝑠𝑖𝑛θ)2 + 6 𝑚𝐿2 𝜃̇ 2 ) = 0.
Con l'approssimazione di piccole oscillazioni (𝑠𝑖𝑛θ~θ) possiamo scrivere:
𝑑
1
1
2
1
𝑚𝑔𝐿
2
2
1
(−𝑚𝑔 𝐿θ + 𝑘(Δ𝑦𝑒𝑞 + 𝐿θ)2 + 𝑚𝐿2 𝜃̇ 2 ) = −
𝜃̇ + 𝑘𝐿 (Δ𝑦𝑒𝑞 + 𝐿θ) 𝜃̇ + 𝑚𝐿2 𝜃̇𝜃̈ = 0
𝑑𝑡
2
2
3
6
2
3
3
3
escludendo la soluzione triviale con 𝜃̇ = 0 otteniamo
−
𝑚𝑔𝐿
2
2
2
1
+ 3 𝐾𝐿 (Δ𝑦𝑒𝑞 + 3 𝐿θ) + 3 𝑚𝐿2 𝜃̈ = 0 da cui otteniamo:
1
4
𝑚𝑔𝐿
2
2 ̈
2
𝑚𝐿
𝜃
+
𝑘𝐿
θ
=
−
𝑘𝐿Δ𝑦𝑒𝑞 . Ricordando ora che
3
9
2
3
𝑚𝑔𝐿
2
2
= 3 𝑘𝐿Δ𝑦𝑒𝑞 esprime la condizione di
equilibrio fra il momento della forza peso ed il momento della forza elastica nella posizione in cui la
sbarra è orizzontale abbiamo:
1 2
4
4
𝑚𝐿 𝜃̈ + 𝑘𝐿2 θ = 𝑚𝜃̈ + 𝑘θ = 0
3
9
3
esattamente come trovato in precedenza.