Quantum Simulators

Università Cattolica del Sacro Cuore
Sede di Brescia
Facoltà di Scienze Matematiche, Fisiche e Naturali
Corso di Laurea di Primo Livello in Fisica
Quantum Simulators
Relatore:
Prof. Fausto Borgonovi
Correlatore:
Prof. Giuseppe Nardelli
Laureando:
Angelo Ziletti
mat. 3404351
Anno Accademico 2007/2008
Prefazione
Il campo dell’informazione quantistica è in rapida evoluzione.
Le potenzialità della computazione quantistica sono immense e qualora venissero effettivamente utilizzate consentirebbero di svolgere compiti che i computer tradizionali non sono, e non saranno mai, in grado di fare.
Lo scopo principale di questa tesi è mostrare come un piccolo registro costituito da 6−10 qubit sia sufficiente a realizzare un simulatore quantistico in grado
di risolvere in modo efficiente problemi standard di meccanica quantistica.
Dato che la natura di un computer quantistico può essere descritta concretamente da un simulatore, ho sviluppato un programma in Fortran capace
di mostrare l’evoluzione di una singola particella governata dall’equazione di
Schrödinger e sottoposta ad un potenziale unidimensionale arbitrariamente
scelto.
Nel capitolo 1 si fornisce una panoramica generale sull’informazione quantistica, presentando al lettore le caratteristiche peculiari, le potenzialità e le
problematiche di questo settore molto fecondo della scienza.
Si prosegue poi introducendo due concetti che stanno alla base dell’informazione quantistica come i qubit e l’entanglement.
Dopo una breve premessa su cosa sia una simulazione quantistica, nel capitolo 5 si espone l’algoritmo effettivamente seguito per sviluppare il codice sorgente in Fortran. Nei capitoli che seguono mostriamo infine il funzionamento
del simulatore, risolvendo alcuni problemi standard di meccanica quantistica
come l’oscillatore armonico, il moto di una particella in un campo uniforme,
le buche di potenziale e l’oscillatore armonico con perturbazione quartica.
ii
Indice
Prefazione
ii
1 Introduzione
1
2 Dai bit ai qubit
7
3 Entanglement
12
3.1
Definizione . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
3.2
Esperimento concettuale di Bohm . . . . . . . . . . . . . . . . 13
3.3
Correlazioni perfette e scoperta di Bell . . . . . . . . . . . . . 15
3.4
Descrizione formale . . . . . . . . . . . . . . . . . . . . . . . . 15
3.5
Realizzazione di uno stato entanglement . . . . . . . . . . . . 19
4 Quantum Fourier Transform
21
4.1
Definizione . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
4.2
Trattazione operatoriale . . . . . . . . . . . . . . . . . . . . . 22
5 Costruzione del Quantum Simulator
26
5.1
Cos’è una simulazione quantistica . . . . . . . . . . . . . . . . 26
5.2
Algoritmo del Quantum Simulator . . . . . . . . . . . . . . . . 29
5.3
Emulazione su un computer classico . . . . . . . . . . . . . . . 35
6 Simulazione di una particella in evoluzione libera
37
6.1
Descrizione del sistema . . . . . . . . . . . . . . . . . . . . . . 37
6.2
Spreading di una funzione d’onda gaussiana . . . . . . . . . . 39
iii
7 Simulazione di un oscillatore armonico
46
7.1
Descrizione del sistema . . . . . . . . . . . . . . . . . . . . . . 46
7.2
Stati coerenti . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
7.3
Stati non coerenti . . . . . . . . . . . . . . . . . . . . . . . . . 56
7.4
7.3.1
Stati di forma gaussiana . . . . . . . . . . . . . . . . . 56
7.3.2
Stati di forma rettangolare . . . . . . . . . . . . . . . . 57
7.3.3
Stati di forma lorenziana . . . . . . . . . . . . . . . . . 58
Onde contropropaganti: interferenza . . . . . . . . . . . . . . 59
8 Simulazione di una particella in un campo uniforme
61
8.1
Descrizione del sistema . . . . . . . . . . . . . . . . . . . . . . 61
8.2
Simulazione . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
9 Simulazione di una particella sottoposta a buche e gradini di
potenziale
9.1
9.2
9.3
67
Barriera di potenziale . . . . . . . . . . . . . . . . . . . . . . . 67
9.1.1
Descrizione del sistema . . . . . . . . . . . . . . . . . . 68
9.1.2
Simulazione . . . . . . . . . . . . . . . . . . . . . . . . 72
Gradino di potenziale . . . . . . . . . . . . . . . . . . . . . . . 74
9.2.1
Descrizione del sistema . . . . . . . . . . . . . . . . . . 74
9.2.2
Simulazione . . . . . . . . . . . . . . . . . . . . . . . . 78
Potenziale deltiforme . . . . . . . . . . . . . . . . . . . . . . . 82
9.3.1
Descrizione del sistema . . . . . . . . . . . . . . . . . . 82
9.3.2
Simulazione . . . . . . . . . . . . . . . . . . . . . . . . 82
10 Simulazione di una particella sottoposta a potenziali anarmonici
84
10.1 Potenziale anarmonico cubico . . . . . . . . . . . . . . . . . . 84
10.2 Potenziale armonico con perturbazione quartica . . . . . . . . 87
11 Conclusioni
89
Appendice - Codice sorgente
91
iv
Capitolo 1
Introduzione
Information is physical
Rolf Landauer
Tutti i sistemi fisici registrano ed elaborano informazione. È da questa
semplice, ma potentissima affermazione che si origina la teoria dell’informazione quantistica. L’idea che l’informazione possa essere manipolata dalla
materia non è del tutto ovvia, ed è entrata a far parte del discorso scientifico
solo da qualche tempo.
Una ventina di anni fa, scienziati come Paul Benioff, Richard Feynman e
David Deutsch, capirono come poter utilizzare la materia per elaborare informazione; all’epoca però, i computer quantistici erano oggetti puramente
astratti, ipotesi non realizzabili praticamente.
Bisogna aspettare i primi anni Novanta del secolo scorso perchè i fisici riescano effettivamente a manipolare singolarmente oggetti quantistici - fotoni,
atomi e ioni per fare alcuni esempi - in modo tale da poterne osservare le
reazioni a determinati stimoli esterni.
Comprendere il comportamento delle particelle quantistiche è però molto
difficile, il loro è un mondo stravagante, molto diverso da quello macroscopico in cui siamo abituati a vivere: particelle che si comportano come onde,
onde che si comportano come particelle, oggetti che stanno in due posti contemporaneamente e cosı̀ via; per darvi un’idea, il premio Nobel Richard P.
1
Feynman con il suo stile provocatorio e irriverente disse: “Posso con certezza
affermare che nessuno capisce la meccanica quantistica”. Muoversi in questo
contesto è piuttosto complicato: cogliere in che modo la realtà registra ed
elabora l’informazione richiede comprendere appieno il linguaggio intrinseco
della natura.
Gli atomi sono piccoli e forti, coriacei e sensibili. Rivolgersi a loro è facile
(picchiate un pugno sul tavolo e ne avrete contattati molti miliardi in un
colpo solo), ma è molto difficile capire le loro risposte (chissà cosa avranno
voluto dire gli atomi del tavolo con quel rumore sordo). Non sono interessati
agli umani, e tendono a farsi gli affari loro. Ma se li toccate nel modo giusto,
se parlate la loro lingua e glielo chiedete per favore, riuscirete a sedurli e a
farli calcolare per voi.
Bene, ma che lingua usare? La lingua della natura, i cui termini sono energia,
forza, impulso, luce, onde sonore, elettricità, gravità e la grammatica è data
dalle sole leggi fisiche. E come è questa lingua? Bizzarra, come il mondo che
descrive, un mondo dove la risposta “sı̀ e no” non è manifestazione di una
palese indecisione, ma una risorsa, una peculiarità che apre orizzonti nuovi,
mai visti prima. Ma come è possibile ciò? Vediamone subito un esempio che
ci interessa particolarmente.
In un calcolatore tradizionale l’unità di informazione, il bit, può assumere
solo due valori: 0 o 1. Nei computer quantistici, invece, il quantum bit o
qubit, può assumere non solo 0 o 1, ma tutti i possibili valori intermedi.
Questa è una conseguenza diretta del principio di sovrapposizione: è possibile costruire stati di sovrapposizione, in cui il qubit ha sia il valore 0 che il
valore 1. A questo punto sorge spontanea una domanda: è possibile sfruttare
le sovrapposizioni quantistiche per eseguire compiti che ai computer classici
sono preclusi? Il primo a porsi la domanda fu David Deutsch a metà degli
anni Ottanta, e la risposta definitiva arrivò qualche anno più tardi: “sı̀, è
possibile”.
Ma come può un computer interpretare il comando dato da un qubit che si
trova in uno stato sovrapposto? Proviamo ad immaginare la situazione. Una
2
parte, quella corrispondente a 0, manda il messaggio “fa questo”, mentre
l’altra parte, quella corrispondente a 1, ordina “fa quello”. Come può il computer quantistico decidere il da farsi? Non deve decidere nulla, fa “questo e
quello” allo stesso tempo! Come un qubit può registrare due valori simultaneamente, cosı̀ un computer quantistico è in grado di svolgere due operazioni
allo stesso tempo. Stupefacente no?
Deutsch ha battezzato questa strana capacità parallelismo quantistico ed è
facile intuire che se si riuscisse a sfruttare al meglio questa peculiarità, nulla
sarà più precluso ai computer quantistici.
Dopo il principio di sovrapposizione, la seconda proprietà su cui si basano i
computer quantistici è il fenomeno dell’entanglement. A livello quantistico
può accadere che due oggetti formino una singola entità, anche se c’è un’arbitrariamente larga separazione fra i due. Ogni tentativo di vedere questa
entità come una combinazione di due oggetti indipendenti fallisce, a meno
che si consideri possibile propagare segnali a velocità superluminali; è a questa conclusione che giunse John Bell nel 1964, ispirandosi al famoso paradosso
EPR sviluppato da Einstein, Podolsky e Rosen nel 1935.
Ma perchè investire tempo e denaro per costruire e studiare i quantum computer? Per molte buone ragioni.
La prima è che dobbiamo farlo se vogliamo continuare ad aumentare la velocità dei computer. La richiesta continua ed incessante di riuscire a trattare
volumi sempre maggiori di informazioni ha imposto una rapida miniaturizzazione dei componenti elettrici, iniziata con la nascita dei transistor e dei
microchip. Questo è evidente dalla legge di Moore.
Già nel 1965, Gordon Moore, cofondatore e presidente di Intel, mentre preparava un discorso per un’azienda notò che le nuove generazioni di chip di memoria venivano presentate sul mercato a intervalli regolari di tre anni. Poichè
ogni nuova generazione aveva una memoria quattro volte più grande della
precedente, il numero di transistor su un chip cresceva in modo costante e
Moore predisse che questo andamento sarebbe continuato per decenni. La
legge di Moore viene spesso presentata dicendo che il numero di transistor su
3
un singolo chip raddoppia ogni 18 mesi. Anche se successivamente il periodo
necessario per il raddoppio si è allungato a due anni, questo processo rimane
comunque stupefacente: non ci sono rami dell’industria in cui i progressi della tecnologia seguono un processo esponenziale, e per cosı̀ tanto tempo.
Ovviamente la legge di Moore non è affatto una legge, ma semplicemente
un’osservazione empirica della velocità con cui i fisici dello stato solido e gli
ingegneri fanno avanzare lo stato dell’arte e una previsione che questo tasso
di sviluppo continuerà nel futuro.
Ma c’è un limite alla miniaturizzazione? Sı̀, ed è proprio a questo punto che
interviene la meccanica quantistica.
Al momento, la corrente - il flusso di elettroni - fra i transistors può essere
paragonata allo scorrere dell’acqua nelle tubature, in accordo con le leggi della
fisica classica. Continuando con la miniaturizzazione, sempre meno elettroni
passeranno attraverso conduttori sempre più sottili. La loro propagazione,
prima o poi, potrà essere descritta solo con le leggi della meccanica quantistica; se consideriamo il trend attuale, si stima che raggiungeremo le dimensioni
atomiche per memorizzare un singolo bit d’informazione attorno al 2020 (attualmente le dimensioni tipiche dei componenti dei circuiti sono dell’ordine
di 100nm).
Un secondo buon motivo per proseguire le ricerche è che un computer quantistico ci permette di studiare il modo in cui l’universo registra ed elabora
l’informazione. Un ottimo modo per capire una legge di natura è costruire
una macchina che la replica. Anzi, avere una macchina che fa una certa cosa
è spesso la molla che ci spinge a comprendere una certa legge: la ruota e
la trottola vengono prima (millenni prima) della conservazione del momento
angolare, la catapulta prima delle leggi di Galileo, il prisma ottico e il telescopio prima dell’ottica newtoniana, la macchina a vapore prima delle leggi
della termodinamica enunciate da Carnot.
Visto che la meccanica quantistica è cosı̀ contro-intuitiva, sarebbe molto formativo costruire un dispositivo che ne incorpora i principi; oggi si producono
computer quantistici “giocattolo” che un giorno ci permetterano di capire in
4
profondità il modo in cui i sistemi fisici registrano ed elaborano informazioni
a livello atomico. Per capire la natura basta replicarla, e per replicarla basta
un computer quantistico.
Un terzo motivo per investire nella ricerca dei computer quantistici è, se
volete, più filosofico: l’utilità dell’inutile. Nella scienza non è raro che speculazioni apparentemente prive di utilità pratica trovino applicazioni a priori
inimmaginabili nei campi più disparati; come non ricordare il grande Micheal
Faraday che, alle incalzanti domande sull’utilità dei suoi esperimenti elettrici da parte del Ministro del Tesoro, rispose: “Un giorno, Vostro Onore,
riscuoterete delle tasse per questo”. Ed in effetti ebbe ragione.
La quantum information quindi è diventata uno dei campi più ferventi della
fisica, con potenzialità tali da rivoluzionare molte aree della scienza, e non
solo. Ci sono però alcuni problemi da tenere bene in considerazione.
Innanzitutto, anche se i computer quantistici fossero già disponibili, il numero di algoritmi di forte interesse è davvero limitato e nulla si può prevedere
sul futuro sviluppo di nuovi algoritmi.
Il secondo tipo di limitazione è che tuttora non sappiamo se un giorno sarà
possibile costruire computer abbastanza grandi per manipolare centinaia di
bit. Il nemico più grande dei computer quantistici è la decoerenza, cioè l’interazione dei qubit con l’ambiente esterno che offusca la tanto delicata quanto importante sovrapposizione degli stati. La decoerenza introduce errori e
idealmente per ovviare a ciò il computer dovrebbe essere completamente isolato dall’ambiente. Questo in pratica vuol dire che l’isolamento deve essere
abbastanza buono da permettere ai codici di correzioni degli errori di eliminare le imperfezioni originatesi nei qubit a causa della decoerenza.
Nonostante tutti questi problemi, si è riusciti a costruire dispositivi capaci
effettivamente di registrare un bit per ogni atomo; essi, però, non hanno ancora raggiunto la capacità di calcolo dei computer classici.
I progressi sono significativi e si susseguono ad un gran ritmo.
Il 13 febbraio 2007, nonostante non fosse creduto possibile prima di 20 anni,
la società canadese D-Wave System ha presentato ORION, il primo computer
5
quantico, dotato di un processore quantistico a 16 qubit, bruciando sul tempo i Bell Labs, tra i più avanzati laboratori di ricerca in questo settore. Poco
tempo dopo, il 15 novembre 2007, sempre la D-Wave System ha presentato
un nuovo quantum processor da 28 qubit.
Tutto questo sta a testimoniare che il settore è in grande fermento e che
progressi fino a poco tempo relegati ad un futuro lontano, potranno presto
divenire realtà.
6
Capitolo 2
Dai bit ai qubit
There are 10 types of people in this world, those who
understand binary code and those who don’t.
Anonymous
Il bit (binary digit) è l’unità minima di informazione nella computazione
classica. Rappresenta una scelta fra due alternative che tradizionalmente si
indicano con 0 e 1, ma che potrebbero essere una qualsiasi coppia in opposizione (bianco-nero, vero-falso ecc.). Vedere che è l’unità minima è molto
semplice; per esempio il risultato di lancio di una moneta è completamente
caratterizzato da un solo bit: testa o croce. Se i lanci sono due, le possibili
alternative diventano quattro, con tre otto e cosı̀ via. Il numero dei possibili
risultati aumenta in modo rapido al crescere dei lanci, cioè dei bit. Con dieci
lanci, per esempio, sono possibili 210 = 1024 risultati, quindi occorreranno
10 bit per rappresentare correttamente il risultato.
Lo stato di un computer classico di n bit è descritto in notazione binaria
tramite un intero k ∈ {0, 1, . . . , 2n − 1} siffatto:
n−1
k = kn−1 2
+ . . . + k1 2 + k0 =
n−1
X
i=0
con kn−1 , . . . , k1 , k0 ∈ {0, 1}.
7
ki 2i
(2.1)
Per esempio, 23 = (10111) è una notazione che sottintende
23 = 1 · 24 + 0 · 23 + 1 · 22 + 1 · 21 + 1 · 20
Nella computazione quantistica, invece, l’unità elementare è il quantum bit o
qubit e un quantum computer può essere visto come un sistema a tanti qubit.
Fisicamente, un qubit è un sistema a due livelli, come per esempio lo spin di
una particella a spin 1/2, la polarizzazione di un singolo fotone o due stati
di un atomo.
Esso può essere descritto in uno spazio di Hilbert complesso bidimensionale.
In questo spazio si può scegliere una coppia di vettori di stato normalizzati
e mutualmente ortogonali, |0i e |1i, per rappresentare i valori 0 e 1 di un bit
classico: questi due stati formano una base. Direttamente dal principio di
sovrapposizione si ha che ogni stato può essere scritto nella forma
|ψi = α|0i + β|1i
(2.2)
Le ampiezze α e β sono dei numeri complessi, soddisfacenti la condizione di
normalizzazione |α|2 + |β|2 = 1. Geometricamente, possiamo interpretare lo
stato di un qubit come un vettore unitario in uno spazio vettoriale complesso
bidimensionale.
La caratteristica di un qubit di trovarsi in una sovrapposizione di stati va
contro il senso comune: ritornando all’esempio precedente, una moneta quantistica vive in una sovrapposizione di “testa e croce”, |0i e |1i, finchè non
viene compiuta una misura; quando questo accade la funzione d’onda collassa ed il risultato può essere solo 0 o 1.
Ora andiamo a ricavare una rappresentazione geometrica per visualizzare un
qubit.
Dato che |α|2 + |β|2 = 1, possiamo riscrivere l’equazione (2.2)
ϑ
ϑ
iγ
iϕ
|ψi = e
cos |0i + e sin |1i
2
2
dove ϑ, ϕ e γ sono numeri reali. Ignorando il termine di fase globale che non
ha significato fisico, possiamo scrivere
ϑ
ϑ
|ψi = cos |0i + eiϕ sin |1i
2
2
8
I numeri ϑ e ϕ definiscono una sfera unitaria tridimensionale come mostrato
in figura (2.1).
Questa sfera prende il nome di sfera di Bloch e fornisce un modo interessante
per visualizzare lo stato di un singolo qubit; inoltre, molte operazioni sui
qubit possono essere visualizzate su di essa. Questa rappresentazione, però,
Figura 2.1: Sfera di Bloch
ha anche una forte limitazione: non esiste una generalizzazione semplice della
sfera di Bloch per più di un qubit.
Quante informazioni possono essere rappresentate con un qubit? Paradossalmente, ci sono infiniti punti sulla sfera unitaria e quindi, in linea di principio si potrebbero memorizzare infinite informazioni. Questa conclusione,
però, è fuorviante perchè non abbiamo tenuto in considerazione che una
misura dello stato del qubit ci restituisce solo i valori 0 e 1. Inoltre, la
misurazione cambia lo stato del qubit, facendo collassare la funzione d’onda
nell’autostato del sistema corrispondente al valore rilevato; questo è una dei
postulati fondamentali della meccanica quantistica. Nel nostro caso, dopo la
misura, il qubit si troverà nell’autostato |0i o nell’autostato |1i e non più in
una loro sovrapposizione.
A questo punto, un’altra interessante domanda può essere formulata: quante
informazioni possono essere rappresentate da un qubit se non lo misuriamo?
9
E come si fa a quantificare una quantità di informazione che non può essere
misurata? Questo è concettualmente molto importante perchè quando un
sistema quantistico chiuso evolve liberamente (senza che vengano effettuate
misure) esso lavora su tutte le possibili sovrapposizioni di stati, non solo
sugli stati |0i e |1i; in questo senso la Natura cela una grande quantità di
informazione. In più, la potenziale quantità di informazione cresce esponenzialmente con il numero di qubit. Vediamolo subito.
Una collezione di n qubit è conosciuta come registro quantistico di dimensione n. La sua corrispondente funzione d’onda risiede in uno spazio di
Hilbert complesso 2n dimensionale.
Lo stato di un quantum computer di n qubit è, contrariamente ai computer
classici (2.1), descritto da:
|ψi =
n −1
2X
ck |ki
(2.3)
k=0
.
dove |ki = |kn−1 i . . . |k1 i|k0 i, con |kj i lo stato del j-esimo qubit; vale inoltre
la condizione di normalizzazione
n −1
2X
|ck |2 = 1
k=0
.
Abbiamo usato la notazione semplificata |ki = |kn−1 i . . . |k1 i|k0 i per il prodotto tensoriale |kn−1 i ⊗ . . . ⊗ |k1 i ⊗ |k0 i.
Il principio di sovrapposizione della meccanica quantistica è chiaramente visibile nell’equazione (2.3): mentre n bit classici possono memorizzare solo un
intero k, il registro quantistico da n qubit si trova nello stato |ki ed inoltre in
una sua combinazione lineare. Per esempio, con un registro classico formato
da 3 bit possiamo rappresentare fino a 8 diversi numeri possibili, cioè esso
può trovarsi in una delle otto possibili configurazioni (000, 001, . . . , 111).
Un registro quantistico composto da tre qubit, invece, sarà in grado di contenere tutti gli 8 numeri contemporaneamente in una sovrapposizione quantistica, cioè tramite una sovrapposizione coerente di stati.
È importante sottolineare che il numero degli stati della base dei qubit in
10
questa sovrapposizione può arrivare fino a 2n , e cresce esponenzialmente con
il numero di qubit.
Il principio di sovrapposizione apre nuove ed incredibili opportunità di calcolo. Quando eseguiamo un’operazione su un computer classico, differenti
input richiedono differenti esecuzioni del programma. Di contro, un computer quantistico può processare contemporaneamente - con una sola esecuzione
- un numero esponenziale di di input. Per darvi un’idea, con un quantum
computer di 300 qubit si possono eseguire allo stesso tempo più operazioni
di quante siano le particelle elementari dell’universo. Grazie al parallelismo
quantistico, basta una piccola macchina con poche centinaia di qubit per
esplorare nello stesso istante un immenso ventaglio di possibilità.
Questa è la potenza della computazione quantistica.
Figura 2.2: Esecuzione di un’operazione logica elementare in un calcolatore
classico e in uno quantistico.
11
Capitolo 3
Entanglement
When two systems, of which we know the states by their respective
representatives, enter into temporary physical interaction due to
known forces between them, and when after a time of mutual
influence the systems separate again, then they can no longer be
described in the same way as before, viz. by endowing each of them
with a representative of its own. I would not call that one but
rather the characteristic trait of quantum mechanics, the one that
enforces its entire departure from classical lines of thought. By
the interaction the two representatives [the quantum states] have
become entangled.
Erwin Schrodinger, 1935
3.1
Definizione
L’entanglement è probabilmente la più spettacolare e controintuitiva manifestazione della meccanica quantistica. Questo fenomeno prevede l’esistenza
di correlazioni non locali fra misurazioni su particelle che hanno interagito
nel passato, ma che al momento della misura possono essere separate da una
distanza arbitrariamente grande. Diciamo che uno stato |ψi a due particelle
è entangled, o non separabile, se non può essere scritto come il prodotto
12
|k1 i|k2 i di due stati che descrivono rispettivamente il primo e il secondo sottosistema, ma solo in una sovrapposizione di questi stati. Per esempio lo
stato di Bell
1
√ (|00i + |11i)
2
è entangled. Se facciamo una misura sul primo qubit, abbiamo due possibili
risultati: 0 con probabilità 1/2, facendo collassare la funzione d’onda nello
stato |ϕ0i = |00i, e 1 ancora con probabilità 1/2 restituendo |ϕ0i = |11i. Il
fatto sorprendente è che una misura sul secondo qubit da sempre lo stesso
risultato ottenuto dalla misura del primo: le misure sono perfettamente correlate, al 100%. Questa correlazione cosı̀ forte, priva di analogo classico ha
suscitato grande interesse nel mondo scientifico ed è stata oggetto di approfonditi studi.
3.2
Esperimento concettuale di Bohm
Figura 3.1: Esperimento concettuale di David Bohm.
Un modo conveniente di discutere l’entanglement è considerare l’esperimento proposto dal fisico americano David Bohn nel 1952. Partiamo da una
particella senza spin. Questa particella è fatta in modo tale da decadere in
due particelle, una di spin 1/2 e l’altra di spin −1/2. Se misuriamo gli spin
delle particelle a una certa distanza dalla sorgente e lungo una certa direzione,
13
essi sono sempre antiparalleli fra loro. Questa è una conseguenza diretta della conservazione del momento angolare in meccanica quantistica. Di primo
acchito il fatto che gli spin delle due particelle debbano essere opposti sembra del tutto innocuo, ma nasconde sorprese incredibili se ci chiediamo lungo
quale direzione queste due particelle hanno lo spin antiparallelo.
Una misura lungo qualunque direzione dello spin ci restituisce sempre o 1/2
o −1/2. Supponiamo di prendere una particella nello stato spin-up lungo la
direzione z e facciamone una misura lungo una nuova direzione, per esempio
y. Come sappiamo dall’esperimento di Stern-Gerlach, lo spin della particella
ha il 50% di probabilità di trovarsi nella nuova direzione e il 50% nella direzione opposta.
Se gli spin possono essere rivolti in una direzione o nell’altra, potrebbe darsi
che siano uguali nei due casi. Questo però è in contraddizione con il fatto che
in ogni misurazione, lungo qualsiasi direzione, gli spin debbano sempre essere opposti. Che cosa risponde la fisica quantistica? In pieno accordo con la
considerazione che tutte le direzioni per lo spin siano ugualmente plausibili,
afferma che le direzioni lungo le quali è orientato lo spin non sono ancora
fissate. Nessuna particella ha uno spin prima di essere misurata. Se però
una delle particelle viene misurata lungo una qualsiasi direzione, soddisfa a
caso una delle due possibilità, cioè di essere parallela o antiparallela rispetto
a questa direzione. L’altra particella, a prescindere dalla distanza, assumerà
esattamente la direzione opposta. La misurazione di una particella quindi
stabilisce automaticamente lo stato in cui si trova l’altra.
Come già accennato in precedenza, i risultati delle misurazioni sono perfettamente correlati se misuriamo lo spin lungo la stessa direzione, ma lo spin delle
singole particelle non può assolutamente essere determinato. Abbiamo cosı̀
due processi casuali, perfettamente legati tra loro a grandi distanze. Einstein
chiamava questo fenomeno “azione fantasma a distanza”e sperava di darne
una spiegazione che si basasse su altri concetti più profondi, ma non vi riuscı̀.
Dio gioca a dadi, e lo fa piuttosto bene.
14
3.3
Correlazioni perfette e scoperta di Bell
L’entanglement restituisce dunque correlazioni perfette. Anche nella fisica
classica e nella realtà quotidiana esistono casi di questo tipo. Il più noto
nella realtà di tutti i giorni è quello dei gemelli monozigoti. Come è risaputo,
essi hanno esattamente le stesse caratteristiche fisiche; oggi sappiamo anche
qual è la causa delle somiglianze tra gemelli: il medesimo patrimonio genetico. Il punto essenziale è che nella realtà quotidiana, le correlazioni perfette
si possono capire facilmente grazie al fatto che due sistemi sono stati creati
con proprietà esattamente uguali, o che almeno le proprietà dei sistemi sono
state fissate dagli stessi meccanismi nascosti.
Sembrerebbe ovvio cercare questi meccanismi nascosti anche nei sistemi della fisica quantistica che presentano correlazioni perfette. Forse le particelle
contengono istruzioni che determinano a priori il risultato di qualsiasi misurazione concepibile? No, non è vero, come dimostra il teorema di Bell.
Esso risponde a questa domanda: è possibile, in linea di principio, spiegare le
correlazioni esistenti tra due sistemi quantistici entangled in base alle caratteristiche dei sistemi stessi? Queste istruzioni sono parametri aggiuntivi che
spesso vengono chiamati variabili nascoste. Bell dimostrò che esiste una contraddizione fra la fisica quantistica e questi modelli a variabili nascoste, detti
anche teorie realistiche locali. In esse le proprietà dei sistemi dipendono solo
da ciò che accade a loro, da quale misurazione viene eseguita; la proprietà osservata è indipendente dalle misurazioni eseguite in altri sistemi. A causa del
fenomeno dell’entanglement, nella fisica quantistica dobbiamo rinunciare al
principio di località e permettere che la misura di un sistema influenzi un’altra effettuata ad una distanza arbitraria, in modo tale da avere correlazioni
perfette.
3.4
Descrizione formale
Dopo aver introdotto l’entanglement da un punto di vista per cosı̀ dire euristico, diamone una caratterizzazione formale. La costruzione matematica
15
di uno stato a due qubit si basa sull’idea del prodotto tensoriale, un’idea che
introduciamo con un semplice esempio.
Denotiamo con HA lo spazio vettoriale bidimensionale delle funzioni fA (x)
con, per esempio, il vettore di base {cos x, sin x}:
fA (x) = λA cos x + µA sin x
e sia HB un’altro spazio vettoriale bidimensionale di funzioni fB (y) con il
vettore di base {cos y, sin y}:
fB (x) = λB cos y + µB sin y
Possiamo costruire una funzione di due variabili chiamata “prodotto tensoriale fra fA e fB ”come:
fA (x) fB (y) =λA λB cos x cos y + λA µB cos x sin y
+ µA λB sin x cos y + µA µB sin x sin y
Una possibile base dello spazio formato dal prodotto tensoriale è:
{cos x cos y, cos x sin y, sin x cos y, sin x sin y}
Ogni funzione in questo spazio può essere decomposta su questa base:
g (x, y) = α cos x cos y + β cos x sin y + γ sin x cos y + δ sin x sin y
ma questa funzione in generale non è esprimibile in termini di prodotto tensoriale fA (x) fB (y). Condizione necessaria e sufficiente affinché questo accada
è αδ = βγ.
Usiamo ora questa procedura per costruire lo stato a due qubit matematicamente. Il primo qubit A vive in uno spazio di Hilbert HA con base ortonormale {|0A i, |1A i}, e il secondo qubit B vive in uno spazio di Hilbert HB con
base ortonormale {|0B i, |1B i}. È naturale rappresentare lo stato fisico in cui
il primo qubit è nello stato |0A i e il secondo è nello stato |0B i con un vettore
16
|X00 i = |0A ⊗ 0B i. Prendendo in considerazione tutti i possibili valori dei
qubit, abbiamo a priori quattro possibilità:
|X00 i = |0A ⊗ 0B i
|X01 i = |0A ⊗ 1B i
|X10 i = |1A ⊗ 0B i
|X11 i = |1A ⊗ 1B i
La notazione ⊗ sta per prodotto tensoriale. È facile costruire uno stato nel
quale il qubit A è nello stato normalizzato
|λA |2 + |µA |2 = 1
|ϕA i = λA |0A i + µA |1A i
e il qubit B è nello stato normalizzato
|λB |2 + |µB |2 = 1
|ϕB i = λB |0B i + µB |1B i
Possiamo denotare questo stato come |ϕA ⊗ ϕB i:
|ϕA ⊗ ϕB i =λA λB |0A ⊗ 0B i + λA µB |0A ⊗ 1B i
+ µA λB |1A ⊗ 0B i + µA µB |1A ⊗ 1B i
= λA λB |X00 i + λA µB |X01 i + µA λB |X10 i + µA µB |X11 i
La corrispondenza con il precedente spazio funzionale è ovvia. Abbiamo
costruito lo spazio HA ⊗ HB come il prodotto tensoriale degli spazi HA e
HB . Il vettore |ϕA ⊗ ϕB i è ancora normalizzato. Esistono varie notazioni per
questi spazi: possiamo trovare appunto |ϕA ⊗ ϕB i, come pure |ϕA i ⊗ |ϕB i o
anche |ϕA ϕB i con il simbolo di prodotto tensoriale omesso.
Il punto cruciale è che lo stato più generale dello spazio HA ⊗ HB non è nella
forma del prodotto tensoriale |ϕA i ⊗ |ϕB i; gli stati della forma |ϕA i ⊗ |ϕB i
sono solo un piccolo sottoinsieme dei vettori di HA ⊗ HB .
Lo stato più generale è della forma
|Ψi =α00 |0A ⊗ 0B i + α01 |0A ⊗ 1B i + α10 |1A ⊗ 0B i + α11 |1A ⊗ 1B i
=α00 |X00 i + α01 |X01 i + α10 |X10 i + α11 |X11 i
La condizione necessaria e sufficiente affinché lo stato |ψi sia della forma
|ϕA ⊗ ϕB i è:
α00 α11 = α01 α10
17
(3.1)
che a priori non è detto che sia soddisfatta.
Diamo un esempio molto semplice di uno stato |Φi che non è nella forma
|ϕA ⊗ ϕB i :
1
|Φi = √ (|0A ⊗ 1B i + |1A ⊗ 0B i)
2
Verifichiamo le relazioni esistenti fra i coefficienti:
(3.2)
1
α01 = α10 = √
2
α00 = α11 = 0
Notiamo che α00 α11 6= α01 α10 .
La condizione espressa dall’equazione (3.1) non è soddisfatta quindi lo stato
preso in esame non è nella forma |ϕA ⊗ ϕB i.
Uno stato a due qubit che non può essere espresso nella forma |ϕA ⊗ ϕB i è
chiamato stato entangled.
Ma come è effettivamente costruito il prodotto tensoriale?
Definiamo il prodotto tensoriale MA ⊗ MB di due operatori MA e MB come
[MA ⊗ MB ]iA pB ;jA qB = [MA ]iA jA [MA ]pB qB
A titolo esemplificativo, consideriamo il prodotto tensoriale di due matrici
2 × 2:
MA =
a b
!
MB =
c d
α β
!
γ δ
La matrice MA ⊗ MB è una matrice 4 × 4, con le righe e le colonne ordinate
come 00, 01, 10, 11:

MA ⊗ MB =
aMB bMB
!
cMB dMB
aα aβ bα bβ



 aγ aδ bγ bδ 

=
 cα cβ dα dβ 


cγ cδ dγ dδ
La proprietà fondamentale di un sistema entangled è la seguente: se |Ψi è uno
stato entangled, allora il qubit A non può essere in uno stato definito |ϕA i.
Verifichiamo ciò in un caso particolare, quello dello stato |Φi dell’equazione
18
(3.2). Assumiamo che M sia una proprietà fisica del qubit A ovvero che M
sia l’operatore autoaggiunto associato alla variabile M agente sul qubit A.
Calcoliamo il valore di aspettazione hΦ|M Φi:
1
hM iΦ =
h0A ⊗ 1B | + h1A ⊗ 0B | | (M 0A ) ⊗ 1B i + | (M 1A ) ⊗ 0B i
2
1
h0A |M 0A i + h1A |M 1A i
=
2
(3.3)
dove abbiamo usato
h0B |0B i = h1B |1B i = 1
h0B |1B i = h1B |0B i = 0.
Ora proviamo che non esiste uno stato
|ϕA i = λ|0A i + µ|1A i
tale che
hΦ|M Φi = hϕA |M ϕA i.
Calcolando il valore di aspettazione di M , otteniamo
hϕA |M ϕA i = |λ|2 h0A |M 0A i+(λ∗ µh0A |M 1A i + λµ∗ h1A |M 0A i)+|µ|2 h1A |M 1A i.
Una condizione necessaria per riprodurre il risultato dell’equazione (3.3)
√
dovrebbe essere |λ| = |µ| = 1/ 2, ma cosı̀ facendo i termini che coinvolgono λ∗ µ e λµ∗ rimangono, in contraddizione con (3.3).
Il risultato ottenuto nell’equazione (3.3) ha una interpretazione fisica molto
semplice: lo stato del qubit A è un mix incorente del 50% dello stato |0A i e
50% dello stato |1A i, e non una sovrapposizione lineare. In generale, non è
possibile descrivere una parte del sistema con un vettore di stato.
3.5
Realizzazione di uno stato entanglement
Ottenere uno stato entanglement partendo da un prodotto tensoriale non è
immediato. È necessario introdurre un’interazione tra i due qubit. Prendiamo come esempio un sistema di due particelle a spin 1/2. Una possibile
19
interazione tra i due spin è:
Ĥ =
~ω
~σA · ~σB
2
Introduciamo l’operatore di SWAP definito come
1
2
(I + ~σA · ~σB ).
Esso agisce su un generico stato |iji nel seguente modo:
1
(I + ~σA · ~σB ) |iji = |jii
2
Da cui otteniamo che
(~σA · ~σB ) |iji = 2|jii − |iji
(3.4)
Si perviene ai seguenti risultati
1
.
(~σA · ~σB ) √ (|10i + |01i) = (~σA · ~σB ) |Φ+ i = |Φ+ i
2
1
.
(~σA · ~σB ) √ (|10i − |01i) = (~σA · ~σB ) |Φ− i = −3|Φ− i
2
I vettori di stato |Φ+ i e |Φ− i sono autovettori di ~σA · ~σB con autovalori
rispettivamente +1 e −3. Partiamo da uno stato non entangled, per esempio
|Φ (t = 0)i = |10i. Per ottenere l’evoluto temporale è sufficiente decomporre
questo stato sugli autostati |Φ+ i e |Φ− i:
1
|Φ (t = 0)i = √ (|Φ+ i + |Φ− i)
2
Applichiamo ora l’operatore di evoluzione temporale
1
e−iĤt/~ |Φ (0)i = √ e−iωt/2 |Φ+ i + e3iωt/2 |Φ− i
2
1
= √ e−iωt/2 e−iωt |Φ+ i + eiωt |Φ− i
2
1
=
e−iωt + eiωt |10i + e−iωt − eiωt |01i
2
= eiωt/2 (cos ωt|10i − i sin ωt|01i) .
Scegliendo ωt = π/4 si ottiene lo stato |Ψi:
1
|Ψi = √ (|10i − i|01i) .
2
Questo è uno stato entangled.
20
Capitolo 4
Quantum Fourier Transform
A good idea has a way of becoming simpler and solving
problems other than that for which it was intended.
Robert Tarjan
4.1
Definizione
Nell’ambito scientifico, uno dei più importanti ed eleganti metodi di risoluzione
dei problemi consiste nel trasformare il problema dato in un altro equivalente
di cui si conosce già la soluzione. Ci sono poche trasformazioni di questo tipo
che appaiono nei contesti più diversi e ci aiutano a risolvere svariati tipi di
problemi. Una grande scoperta della computazione quantistica è stata che
alcune di queste trasformazioni possono essere compiute molto più velocemente su un computer quantistico rispetto ad un computer classico, fatto
che ha permesso la costruzione di algoritmi efficienti da utilizzare su computer quantistici.
Una di queste trasformazioni è la trasformata di Fourier discreta (DFT).
Nell’usuale notazione matematica, la trasformata di Fourier discreta prende
in input un vettore di numeri complessi, x0 , . . . , xN −1 dove la lunghezza N
del vettore è un parametro fissato. In output la DFT restituisce un altro
21
vettore di numeri complessi y0 , . . . , yN −1 definito da
N −1
. 1 X
yk = √
xj e2πijk/N
N j=0
La trasformata di Fourier quantistica è esattamente la medesima trasformazione, anche se la notazione è un po’ differente. La trasformata di Fourier
quantistica di una base ortonormale |0i, . . . |N − 1i è definita come un operatore lineare che agisce sugli stati di base nel seguente modo
N −1
1 X 2πijk/N
|ji −→ √
e
|ki
N k=0
(4.1)
In maniera del tutto analoga, l’azione su uno stato arbitrario può essere
descritta come
N
−1
X
xj |ji −→
j=0
N
−1
X
yk |ki
(4.2)
k=0
dove i coefficienti yk sono ottenuti applicando la DFT ai coefficienti xj .
Non è ovvio dalla definizione, ma questa trasformazione è unitaria e quindi
può essere utilizzata in algoritmi per computer quantistici; questo è proprio
quello che faremo nel capitolo 5 dove utilizzeremo la DFT nell’algoritmo
che simula il comportamento di una particella quantistica sottoposta ad un
potenziale arbitrariamente scelto.
4.2
Trattazione operatoriale
Diamo ora una descrizione della trasformata di Fourier in termini di operatori
quanto-meccanici. L’idea è che nell’effettiva implementazione in un computer quantistico gli operatori corrispondano a porte logiche, atte a compiere
precise operazioni sui qubit. Assumiamo di avere un registro quantistico
composto da L qubit che quindi può contenere un qualsiasi numero x, da 0
a 2L − 1. Ogni numero decimale può essere espresso nello stato
|xi = |xL−1 xL−2 . . . x1 x0 i = |xL−1 i ⊗ |xL−2 i ⊗ . . . |x1 i ⊗ |x0 i
22
(4.3)
dove
x=
L−1
X
xi 2i
(xi = 0, 1)
i=0
Introduciamo l’operatore Aj che agisce solo sul j-esimo qubit. Questo operatore “mescola” in un modo opportuno i due stati di base, |0j i e |1j i, del
j-esimo qubit. La forma esplicita dell’operatore Aj è
1
Aj = √ |0j ih0j | + |0j ih1j | + |1j ih0j | − |1j ih1j |
2
(j = 0, . . . , L − 1) .
Definiamo ora un operatore a due qubit che agisce sugli stati j-esimo e k-esimo
nel modo seguente:
Bjk = |0jk ih0jk | + |1jk ih1jk | + |2jk ih2jk | + eiθjk |3jk ih3jk |
θjk =
(4.4)
π
2k−j
In (4.4) è stata usata la seguente notazione:
|0jk i = |0j 0k i
|1jk i = |0j 1k i
|2jk i = |1j 0k i
|3jk i = |1j 1k i
Vediamo l’azione dell’operatore Aj :
1
Aj |0j i = √ |0j i + |1j i
2
1
Aj |1j i = √ |0j i − |1j i
2
e dell’operatore Bjk :
Bjk |0jk i = |0jk i
Bjk |2jk i = |2jk i
Bjk |1jk i = |1jk i
iπ
Bjk |3jk i = exp k−j |3jk i
2
È evidente che l’operatore Bjk cambia solo lo stato
|3jk i = |1j , 1k i
23
(4.5)
(4.6)
modificandone la fase. Gli operatori quanto-meccanici Aj e Bjk permettono
di eseguire la DFT di una funzione d’onda. Per far ciò, si applica l’operatore AL−1 allo stato |xi. Poi si applica (AL−2 BL−2,L−1 ) allo stato risultante.
Dopodiché si applicano i seguenti operatori
AL−3 BL−3,L−2 BL−3,L−1
AL−4 BL−4,L−3 BL−4,L−2 BL−4,L−1
e cosı̀ via. Nell’esempio considerato applicheremo tre gruppi di operatori:
A2 , poi (A1 B12 ) ed infine (A0 B01 B02 ). In totale quindi dovremo pervenire a
A0 B01 B02 A1 B12 A2 |xi
(4.7)
A titolo esemplificativo consideriamo lo stato
|xi = |2i = |x2 x1 x0 i = |010i
(4.8)
Primo step:
1
A2 |xi = A2 |2i = A2 |x2 i|x1 i|x0 i = A2 |0i|1i|0i = √ |0i + |1i |1i|0i
2
Secondo step:
1
1
iπ/2
B12 A2 |2i = B12 √ |0i + |1i |1i|0i = √ |0i|1i|0i + e |1i|1i|0i
2
2
Terzo step:
1
iπ/2
A1 B12 A2 |2i =
|0i |0i − |1i |0i + e |1i |0i − |1i |0i =
2
1
iπ/2
iπ/2
=
|0i|0i|0i − |0i|1i|0i + e |1i|0i|0i − e |1i|1i|0i
2
L’operatore B02 non cambia lo stato ottenuto perchè opera solo sugli stati
|1k1i. Anche l’operatore B01 non modifica nulla dell’ultimo stato perchè
agisce solo sugli stati della forma |k11i.
24
Non ci resta che applicare l’operatore A0
1
A0 B01 B02 A1 B12 A2 |2i =
|0i|0i |0i + |1i − |0i|1i |0i + |1i +
2
iπ/2
iπ/2
e |1i|0i |0i + |1i − e |1i|1i |0i + |1i =
1
|000i + |001i − |010i + |011i +
=√
8
i |100i + |101i − i |110i + |111i
Adesso “invertiamo” i qubit (ovvero, per il caso di tre qubit, eseguiamo la
trasformazione |ijki → |kjii) ed arriviamo alla funzione d’onda finale
1
√
|000i + |100i − |010i + |110i + i |001i + |101i − i |011i + |111i
8
In notazione decimale il nostro stato è
1
√
|0i + |4i − |2i + |6i + i |1i + |5i − i |3i + |7i
8
(4.9)
È facile verificare che l’equazione (4.9) è la trasformata di Fourier discreta
di (4.8). ll nostro gruppo di operatori (4.7) esegue quindi una DFT.
Facciamo notare che per eseguire la trasformata di Fourier di L qubit servono
L operazioni Aj e [L (L − 1) /2] operazioni Bjk . Il numero di step necessari
è perciò O (L2 ).
25
Capitolo 5
Costruzione del Quantum
Simulator
In natural science, Nature has given us a world and we’re
just to discover its laws. In computer, we can stuff laws into
it and create a world.
Alan Kay
The best way to predict the future is to implement it.
David Heinemeier Hansson
5.1
Cos’è una simulazione quantistica
Comprendere a fondo la Natura è l’intendimento di tutti i fisici. Gli scienziati
pongono domande all’Universo, investigano ed elaborano teorie con l’obiettivo di capire il significato più recondito dei fenomeni fisici, costruendo modelli
che li possano spiegare con eleganza e naturalezza.
Molte volte capita di giungere ad una legge, ad una equazione che ci permette di condensare in essa tutta la dinamica del sistema esaminato; per
esempio, in meccanica classica abbiamo la legge di Newton, in elettrostatica
la legge di Poisson, in elettrodinamica l’equazione delle onde e in meccanica
quantistica l’equazione di Schrödinger. In ogni campo, la questione è sempre
26
la medesima: dato uno stato iniziale, si deve determinare quale sarà lo stato
del sistema dopo un generico istante di tempo.
Rispondere a questa domanda è in teoria semplice, ma in pratica molto difficile. Semplice perchè, nota la dinamica del sistema considerato, sappiamo
tutto su come evolve, basta trovare le soluzioni delle equazioni differenziali.
Ed è proprio questo il punto: risolvere equazioni. Questo ambito è molto
problematico, soprattutto se si considera che il più delle volte non esistono
metodi generali per trovare soluzioni al problema dato. È logico, d’altro
canto, che dobbiamo pur sfruttare in qualche maniera le informazioni che ci
forniscono queste equazioni. Il procedimento che si segue è l’approssimazione.
Le soluzioni che descrivono la dinamica del sistema sono ottenute approssimando lo stato con una rappresentazione digitale, discretizzando nello spazio
e nel tempo l’equazione differenziale da risolvere. Poi si procede per via iterativa, applicando una procedura che, nello spazio discretizzato, ci conduca
step by step dallo stato iniziale a quello finale.
Ovviamente questo modo di procedere introduce degli errori ; sarà cura dell’analista numerico garantirci che l’errore sia limitato e che cresca poco all’aumentare del numero di iterazioni in modo da rendere il metodo fruibile
e sensato. Alcuni sistemi dinamici però non possono essere simulati su computer classici in modo efficiente ed i sistemi quantistici ne sono un esempio.
La legge che sta alla base del mondo microscopico è l’equazione di Schrödinger:
i~
∂
|ψi = Ĥ|ψi
∂t
(5.1)
È un’equazione alle derivate parziali di tipo ellittico, molto simile all’equazione della diffusione1 la cui risoluzione non pone particolari problemi.
Il problema è che per simulare un sistema quantistico dobbiamo risolvere un
numero in genere esponenzialmente grande di equazioni differenziali ordinarie. Una particella con spin 1/2 che evolve secondo l’equazione di Schrödinger
1
Per consentire un confronto immediato riportiamo l’equazione di diffusione:
~ 2 ϕ = 1 ∂ϕ
∇
a2 ∂t
27
ci conduce ad un sistema di due equazioni differenziali, per due particelle
quattro equazioni; e per n particelle, 2n equazioni. Bastano quindi dieci
o venti particelle per rendere di dimensioni titaniche i sistemi da risolvere,
rispettivamente formati da 1.024 e 1.048.576 equazioni.
In generale, per seguire l’evoluzione di un sistema quantistico, un computer
classico deve assegnare un’operazione specifica a tutte le componenti della
funzione d’onda, ma come già detto il numero di queste operazioni cresce
esponenzialmente al crescere delle dimensioni del sistema. I computer classici quindi non riescono a riprodurre con efficienza il mondo microscopico,
ma può farlo un computer quantistico. Essendo di per sé un sistema fisico, è
sufficiente mettere in corrispondenza biunivoca le varie parti del sistema da
simulare con i qubit di un computer quantistico: le interazioni fisiche diventano cosı̀ operazioni logiche, e la simulazione è cosı̀ precisa che i due oggetti
(il computer e il sistema da simulare) si comportano esattamente allo stesso
modo, tanto da diventare a tutti gli effetti indistinguibili.
La simulazione è efficiente, in due sensi: il numero di qubit necessari è uguale
al numero di qubit del sistema da simulare e il numero di operazioni elementari richieste è proporzionale al tempo in cui si svolge l’evoluzione del sistema.
In primo luogo, si deve scomporre il sistema nelle sue componenti, cioè lo si
deve dividere in un numero di qubit sufficiente a descrivere le sue caratteristiche e la sua evoluzione. In secondo luogo, si devono far corrispondere le
interazioni tra le parti ad altrettante operazioni logiche tra i qubit.
La potenza della simulazione da parte di un quantum computer si può apprezzare ancor di più prendendo in considerazione la distinzione tra digitale e
analogico. Le variabili della fisica classica, cioè quantità come posizione, velocità, energia sono continue. Un computer digitale classico utilizza variabili
discrete, i bit. Per trattare una quantità continua, un calcolatore digitale
deve prima discretizzarla. In un computer quantistico non c’è nessuna distinzione tra analogico e digitale. I quanti sono discreti per definizione, e si
può instaurare una corrispondenza biunivoca tra i loro stati e gli stati dei
qubit, in modo naturale e senza fare approssimazioni. I qubit però hanno
28
anche natura ondulatoria, e quindi sono variabili continue il che permette
loro di essere sovrapposizioni continue di stati.
Onde e particelle: concetti diversissimi che grazie alla relazione di De Broglie
vengono uniti in modo indissolubile.
5.2
Algoritmo del Quantum Simulator
In questa sezione descriveremo l’algoritmo del quantum simulator. Lo scopo
principale di questo lavoro è mostrare come effettivamente operi un computer
quantistico, emulando il suo funzionamento con un programma in Fortran.
Arriveremo a mostrare come un registro da 6 - 10 qubit sia in grado di
risolvere in modo efficiente problemi standard di meccanica quantistica.
Data l’equazione di Schrödinger
i~
∂
|ψi = Ĥ|ψi
∂t
(5.2)
e supposta l’hamiltoniana indipendente dal tempo, troviamo che un generico
stato al tempo t può essere ottenuto applicando l’operatore di evoluzione
temporale Ut al ket iniziale:
|ψ (t)i = Ût |ψ (0)i = e−iĤt/~ |ψ (0)i
(5.3)
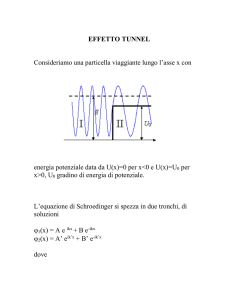
Consideriamo un moto quanto-meccanico di una particella in una dimensione;
l’equazione di Schrödinger diventa
i~
∂
ψ (x, t) = Ĥψ (x, t)
∂t
(5.4)
dove l’hamiltoniana Ĥ è data da
Ĥ = Ĥ0 + V̂ (x) = −
e V̂ (x) è un potenziale unidimensionale.
29
~2 ∂ 2
+ V̂ (x)
2m ∂x2
(5.5)
Discretizzazione
Per risolvere l’equazione (5.4) su un quantum computer con un numero finito
di risorse (un numero finito di qubit e una sequenza altrettanto finita di
quantum gate) dobbiamo prima discretizzare le variabili continue x e t.
Se il moto si svolge in una regione finita, diciamo −d ≤ x ≤ d, decomponiamo
questa regione in 2n intervalli di lunghezza
∆x =
2d
2n
(5.6)
Rappresenteremo questi intervalli nello spazio di Hilbert di un registro quantistico di n qubit. Da ciò notiamo un fatto molto vantaggioso: lo step di
discretizzazione decresce esponenzialmente con il numero di qubit.
Per esempio, considerando come regione da simulare −5 ≤ x ≤ 5, otteniamo
∆x ≈ 0.156 e ∆x ≈ 0.039 rispettivamente utilizzando 6 e 8 qubit.
La funzione d’onda ψ (x, t) è approssimata da
n −1
2X
k=0
dove
n
2 −1
1 X
ck (t) |ki =
ψ (xk , t) |ki
N k=0
1
xk = −d + k +
∆x,
2
(5.7)
(5.8)
|ki = |kn−1 i|kn−2 i . . . |k0 i è lo stato della base associata al registro quantistico
da n qubit, e il fattore
v
u2n −1
uX
N ≡t
|ψ(xk , t)|2
(5.9)
k=0
assicura che la funzione d’onda discretizzata sia normalizzata. L’equazione
(5.7) fornisce una buona approssimazione di |ψi quando la discretizzazione
∆x è molto più piccola delle dimensioni caratteristiche del sistema2 da considerare.
2
Le dimensioni caratteristiche di un sistema determinano le condizioni di un dato prob-
lema concreto, dando un’indicazione su quale sia la scala spaziale del sistema fisico da
considerare; un esempio di dimensione caratteristica può essere il range di variazione del
potenziale.
30
Evoluzione temporale
L’equazione (5.4) può essere formalmente integrata propagando la funzione
d’onda iniziale ψ (x, 0) per ogni step ε come segue:
ψ (x, t + ε) = e−i(Ĥ0 +V̂ (x))ε/~ ψ (x, t)
(5.10)
Non è detto che gli operatori Ĥ0 e V̂ commutino. In generale infatti si ha
che
e−i(Ĥ0 +V̂ )t/~ 6= e−iĤ0 t/~ e−iV̂ t/~
(5.11)
A questo punto però si può applicare la Trotter decomposition, un teorema
di approssimazione asintotico che è alla base degli algoritmi di simulazione
quantistica.
Teorema: Trotter decomposition
Siano Â e B̂ due operatori hermitiani. Allora per ogni t reale,
n
lim eiÂt/n eiB̂t/n = ei(Â+B̂ )t
n→∞
(5.12)
Dimostrazione.
Per definizione
iÂt/n
e
e inoltre
iÂt/n iB̂t/n
e
e
1
1
= I + iÂt + O 2
n
n
1 1
= I + i Â + B̂ t + O 2
n
n
Da cui
iÂt/n iB̂t/n n
e
e
Considerando che
n k
X
1
n 1 +
O
=I+
i
Â
+
B̂
t
n
k nk
k=1
n 1
1
1
=
1+O
k
k n
k!
n
arriviamo a
lim
n→∞
eiÂt/n eiB̂t/n
n
k
n
i Â + B̂ t X
1
1
= lim
1+O
+O
= ei(Â+B̂ )t
n→∞
k!
n
n
k=0
31
Come possiamo notare non c’è nessuna
ipotesi
sul commutatore di Â e B̂
h
i
quindi questo risultato vale anche se Â, B̂ 6= 0, anzi è proprio per questo
che è tanto importante.
Ovviamente vale anche la seguente relazione:
ei(Â+B̂ )∆t = eiÂ∆t eiB̂∆t + O ∆t2
Ritorniamo ora al problema da noi considerato cioè
ψ (x, t + ε) = e−i(Ĥ0 +V̂ (x))ε/~ ψ (x, t) .
Se ε è sufficientemente piccolo possiamo scrivere
e−i(Ĥ0 +V̂ (x))ε/~ ≈ e−iĤ0 ε/~ e−iV̂ (x)ε/~
oppure in maniera del tutto analoga
e−i(Ĥ0 +V̂ (x))ε/~ ≈ e−iV̂ (x)ε/~ e−iĤ0 ε/~
(5.13)
In entrambe le scritture si compie un errore O (ε2 ) se gli operatori Ĥ0 e V̂
non commutano. L’operatore alla destra dell’uguale nell’equazione (5.13) è
ancora unitario ed è molto più facile da trattare numericamente di quello a
sinistra. Il nostro problema ora si riconduce ad applicare due operatori: Ĥ0
(particella libera) e V̂ (potenziale unidimensionale).
Operatore H0 (particella libera)
Dobbiamo dapprima applicare l’operatore e−iĤ0 ε/~ . Sappiamo che l’operatore
momento nello spazio delle configurazioni ha la seguente forma:
hx|P̂ |ψi = −i~
∂
∂
hx|ψi = −i~ ψ (x)
∂x
∂x
(5.14)
facilmente generalizzabile anche per una potenza n-esima di P̂ :
hx|P̂ n |ψi = (−i~)n
n
∂n
n ∂
hx|ψi
=
(−i~)
ψ (x)
∂xn
∂xn
Dato che l’hamiltoniana di una particella libera è Ĥ0 =
p̂2
,
2m
nello spazio
delle configurazioni questo operatore è un operatore di derivata seconda.
32
Chiaramente, la derivazione è un’operazione molto delicata dal punto di vista
computazionale perchè essa implica un passaggio al limite che porta con sé
inevitabili errori di approssimazione. Per evitare di compiere operazioni di
derivazione passiamo nello spazio degli impulsi. Nello spazio dei momenti
infatti l’operatore P̂ non è più un operatore di derivazione, ma si riduce ad
un operatore di moltiplicazione. Inizialmente, la nostra funzione d’onda è
scritta nello spazio delle configurazioni:
Z
|ψi = |xihx|ψidx
Troviamo la rappresentazione di |ψi nello spazio dei momenti moltiplicando
per il bra hp|:
Z
hp|ψi =
Z
hp|xihx|ψidx =
hp|xiψ (x) dx
(5.15)
Sappiamo inoltre che gli autostati del momento nello spazio delle configurazioni sono delle onde piane3 , cioè
hx|pi = √
i
1
e− ~ px
2π~
Sostituendo in (5.15) otteniamo:
Z − i px
e ~
√
hp|ψi =
ψ (x) dx = ψe (p)
2π~
(5.16)
Questa non è altro che la trasformata di Fourier. Dall’equazione (5.16) si
ricava che
F [ψ (x)] = ψe (p)
3
(5.17)
Per dimostrarlo utilizziamo (5.14) scegliendo |ψi autoket |pi dell’impulso; otteniamo
hx|p̂|pi = −i~
cioè
∂
hx|pi
∂x
∂
hx|pi
∂x
Questa è un’equazione differenziale del primo ordine la cui soluzione è
ipx
hx|pi = N exp −
~
phx|pi = −i~
Infine N si ricava facilmente scrivendo hp0 |pi.
33
La trasformazione che ci permette di passare dalla spazio delle coordinate a
quello dei momenti è la trasformata di Fourier. Sappiamo inoltre che vale
l’identità di Parseval che ci garantisce l’identità della norma nei due spazi:
2
e
kψ(x)k2 = kψ(p)k
e quindi possiamo continuare a dare al modulo quadro della funzione d’onda
un’interpretazione legata alla probabilità.
Tutte le considerazioni fatte finora continuano a valere anche per il caso discreto: basta infatti sostituire gli integrali con sommatorie e tutto vale in
maniera analoga. L’idea quindi è la seguente: eseguire dapprima la trasformata di Fourier per passare dalla rappresentazione delle configurazioni a quella dei momenti, poi applicare l’operatore di evoluzione libera che in questo
spazio è di moltiplicazione, ed infine applicare la trasformata di Fourier inversa per ritornare nello spazio di partenza, ovvero quello delle configurazioni.
L’operatore H0 si può quindi riscrivere nel seguente modo:
e−iH0 ε/~ = F −1 e−i(p
2 /2m
)ε/~ F
(5.18)
dove con F si indica l’operatore che esegue la trasformata di Fourier.
Ricordiamoci ora che il nostro sistema è discreto quindi F sta a rappresentare la trasformata di Fourier quantistica; in più facciamo notare che essa
può essere efficientemente implementata in un computer quantistico come
dimostrato nel capitolo 4.
Operatore V̂ (x) (potenziale unidimensionale)
Dopo aver applicato l’operatore dell’equazione (5.18) la nostra funzione d’onda è nello spazio delle coordinate. In questo spazio l’operatore V̂ (x) è un
operatore di moltiplicazione. Concludendo, la funzione d’onda ψ (x, t) al
tempo t = kε si ottiene (a meno di un O (ε2 )) dalla funzione iniziale ψ (x, 0)
applicando l’operatore unitario
e−iV (x)ε/~ F −1 e−i(p
34
2 /2m
)ε/~ F
(5.19)
k volte. La simulazione dell’equazione di Schrödinger è perciò ridotta all’implementazione della trasformata di Fourier (e della sua inversa) e quindi
all’applicazione di operatori della forma
|xi −→ eif (x) |xi
(5.20)
Facciamo notare infatti che sia Ĥ0 che V̂ sono della forma (5.20), dove il
primo è scritto nella rappresentazione dei momenti.
5.3
Emulazione su un computer classico
Per illustrare il funzionamento di un quantum simulator, lo emuliamo su un
computer classico, pagando però come pegno un decadimento esponenziale
delle prestazioni rispetto ad una vera computazione quantistica. L’inefficienza di una simulazione classica è dovuta al fatto che per replicare l’azione
di un’elementare porta quantistica su un computer tradizionale, abbiamo
bisogno di calcolare tutti i 2n coefficienti della funzione d’onda descritti nell’equazione (5.7); ricordiamo infatti che n è il numero dei qubit del registro
quantistico considerato.
Un’altra differenza fondamentale fra la computazione classica e quella quantistica è l’accesso ai dati. In una simulazione quantistica, contrariamente a
ciò che accade classicamente, non possiamo determinare la funzione d’onda
ψ (x, t) dopo una singola simulazione. Ogni run è seguito dalla proiezione
della funzione d’onda sulla base degli stati computazionali, operazione che
da come risultato xk con probabilità |hk|ψ (x, t)i|2 . Di conseguenza, la distribuzione di probabilità |ψ (x, t) |2 può essere ricostruita, a meno di errori
statistici, solo se la simulazione è ripetuta molte volte. Se il risultato xk
è ottenuto Mk volte in M esecuzioni, possiamo stimare la probabilità nel
seguente modo:
n
2 −1
Mk X
|ψ (x, t) | = N
|ψ(xk , t)|2
=
M
M k=0
2
2 Mk
(5.21)
dove si è utilizzato il fattore di normalizzazione N definito nell’equazione
(5.9).
35
Nei capitoli che seguono simuleremo problemi elementari di meccanica quantistica, utilizzando il quantum simulator appena costruito.
36
Capitolo 6
Simulazione di una particella in
evoluzione libera
Computer programming is an art form, like the creation of
poetry or music.
Donald Knuth
6.1
Descrizione del sistema
In questo capitolo simuleremo l’evoluzione del sistema in assoluto più semplice cioè una particella in evoluzione libera. L’hamiltoniana associata a
questo sistema è la seguente:
p̂2
(6.1)
2m
Ovviamente la dinamica classica è chiarissima: la particella si muove di moto
Ĥ =
rettilineo uniforme. Per trovare ciò introduciamo un apparato formale che
all’inizio sembrerà una superflua complicazione, ma che nel seguito si rivelerà
molto utile per calcolare l’indeterminazione del sistema. Dato ÂH un operatore nella rappresentazione di Heisenberg, l’equazione di Heisenberg si può
scrivere nella seguente forma:
i
∂ ÂH
1 h
(t) =
ÂH (t) , Ĥ
∂t
i~
37
(6.2)
Essa ci fornisce la dinamica del nostro sistema in termini di operatori.
Applichiamo ora l’equazione (7.7) alle variabili dinamiche del nostro sistema,
ovvero a x̂ e p̂.
Cominciamo dall’operatore p̂.
i
∂ p̂ h
1 2
i~
= p̂, Ĥ =
p̂, p̂ = 0
∂t
2m
L’operatore p̂ è una costante del moto, come ci aspettavamo.
Applichiamo ora l’equazione di evoluzione di Heisenberg per l’operatore x̂:
i
∂ x̂ h
1
1 2
p̂
i~
= x̂, Ĥ =
x̂, p̂ =
2p̂i~ = i~
∂t
2m
2m
m
Ne risulta:
p̂
p̂ (0)
∂ x̂
=
=
∂t
m
m
dove si è utilizzata l’informazione che p̂ è costante del moto.
Integrando l’equazione differenziale troviamo
p̂ (0)
x̂ (t) = x̂ (0) +
t
(6.3)
m
ovvero gli operatori quantistici si muovono, in analogia con le variabili dinamiche classiche, di moto rettilineo uniforme.
Ora calcoliamo l’indeterminazione del nostro sistema. Il commutatore dell’operatore posizione per tempi diversi è diverso da zero; nello specifico
p̂ (0)
t
i~t
[x̂ (t) , x̂ (0)] = x̂ (0) +
t, x̂ (0) =
[p̂ (0) , x̂ (0)] = −
(6.4)
m
m
m
Questo commutatore cresce linearmente con il tempo. Possiamo ora applicare la relazione di indeterminazione di Heisenberg a questi due operatori
ottenendo
2
2
h(∆x) it h(∆x) it=0
2 ~2 t2
1 ≥ h x̂ (t) , x̂ (0) i =
4
4m2
(6.5)
Da cui troviamo lo sparpagliamento (“spreading”) della posizione al tempo
t:
~t
1
(6.6)
2m ∆x (0)
Questa relazione implica che tanto più la particella è localizzata all’istante ini∆x (t) ≥
ziale, tanto più la sua indeterminazione diventa grande durante l’evoluzione.
Inoltre, lo spreading cresce linearmente con il tempo.
38
6.2
Spreading di una funzione d’onda gaussiana
Consideriamo dapprima il caso in cui lo stato iniziale sia di forma gaussiana:
(x − x0 )2
1
exp −
(6.7)
ψ (x, 0) =
2σ 2
(π)1/4 (σ)1/2
Applicando l’operatore di evoluzione temporale Ut = e−iĤt/~ allo stato iniziale, dopo qualche conto troviamo:
r

!
p0 t 2
2
4σ
x
−
1
1
m
 exp −
q
|ψ(x, t)|2 = 
2 2
πσ 2 1 + ~t2
4σ 4 + 4~m2t
(6.8)
m2 σ 4
ovvero una gaussiana centrata in x̄ =
p0 t
.
m
Il centro della gaussiana si muove dunque di moto rettilineo uniforme; calco2
. Si ha che:
liamone la varianza σX
2
σX
(t) =
Da cui otteniamo
σ2
~2 t2
+
2
2m2 σ 2
s
~2 t2
σX (t) = σX (0)
1+ 2 4
mσ
(6.9)
(6.10)
La varianza cresce linearmente con il tempo. Man mano che il tempo cresce
si perdono tutte le informazioni sul sistema perché la particella si sparpaglia
e si ottiene ben presto una probabilità uniforme di trovarla dappertutto.
Simulazione
Simuliamo ora questo sistema con il quantum simulator. Per semplicità, in
tutte le simulazioni considereremo ~ = m = 1. Indichiamo con ε lo step
temporale e con k il numero totale di step temporali considerati. Dove non
diversamente specificato, abbiamo utilizzato per la simulazione 8 qubit.
Possiamo notare dal grafico proposto in figura (6.1) l’aumento dello spreading con il tempo; già in un piccolo intervallo di tempo la particella si è sparpagliata notevolmente. Cerchiamo di dare una caratterizzazione quantitativa
39
(a) Grafico 3D
(b) Grafico 2D
Figura 6.1: Funzione d’onda gaussiana in evoluzione libera. Parametri: σin = 0.5,
ε = 0.01, k = 120, x0 = 0
40
a questo fenomeno, calcolando l’indeterminazione della funzione d’onda ad
ogni step temporale considerato. La varianza di un operatore è cosı̀ definita:
∆A2 = hA2 i − hAi2
Calcoliamo la varianza dell’operatore x̂ sullo stato |ψi. Il valor medio dell’operatore x̂ sullo stato |ψi
Z
hxi = hψ|x|ψi =
x|ψ (x, t)|2 dx
ed il secondo momento della distribuzione
Z
2
2
hx i = hψ|x |ψi = x2 |ψ (x, t)|2 dx
Il nostro problema però è discretizzato, quindi gli integrali diventano sommatorie nella variabile della discretizzazione j. La varianza dell’operatore x̂
ha la seguente forma:
!2
∆x2 =
X
x2 |ψ (x, t)|2 −
X
j
x|ψ (x, t)|2
(6.11)
j
Analogamente si procede per l’operatore p̂ e si calcola l’indeterminazione
∆x∆p. Il risultato trovato è esposto in figura (6.4). Esso è in completo accordo con l’espressione dell’indeterminazione che si ricava facilmente
dall’equazione (6.10):
s
~2 t2
1+ 2 4
mσ
s
~2 t2
= ∆p (0) ∆x (0)
1+ 2 4
mσ
~ σ
∆x (t) ∆p (t) = √ √
σ 2 2
(6.12)
dove abbiamo utilizzato che il ∆p è costante nel tempo.
A questo punto cerchiamo di fare un parallelismo con la meccanica classica.
Supponiamo di prendere uno sciame di particelle classiche entro l’intervallo ∆x∆p e di valutare lo sparpagliamento dello sciame al tempo t. Ogni
particella si muove di moto rettilineo uniforme
x=
p
t
m
41
Figura 6.2: Andamento dell’indeterminazione della funzione d’onda gaussiana
mostrata in figura (6.1) in evoluzione libera. In blu il caso quantistico trovato con
il simulatore ed in rosso lo spreading classico: per grandi tempi gli sparpagliamenti
coincidono.
Se si considera un’incertezza sul momento δp si ha un’incertezza sulla posizione:
δp
t
m
Supponendo che l’incertezza in p sia la stessa del pacchetto quantistico
δxclassico =
otteniamo:
~ t
σm
che è l’andamento dello sparpagliamento quantistico per tempi molto grandi.
δxclassico =
Cerchiamo ora lo stato per cui lo spreading è il minimo possibile. Dall’equazione (6.12) è infatti facile rendersi conto che la Gaussiana da considerare
è quella con σ = 1. Con questa scelta del parametro σ le indeterminazioni in
√
x e in p sono le stesse e valgono 1/ 2. Se già dalla figura (6.3) possiamo intuire che lo spreading della funzione d’onda è molto piccolo nel caso di minima
indeterminazione, nel grafico (6.4) ne abbiamo una conferma quantitativa.
Concludiamo questa sezione analizzando l’andamento dell’indeterminazione
42
(a) Grafico 3D
(b) Grafico 2D
Figura 6.3: Pacchetto gaussiano di minima indeterminazione in evoluzione libera.
Parametri: σin = 1, ε = 0.01, k = 120, x0 = 0
43
Figura 6.4: In viola l’andamento dell’indeterminazione del pacchetto gaussiano
con σ = 1 mostrato in figura (6.3). In blu riportiamo per un confronto il pacchetto
(σ = 0.5) di figura (6.1).
al variare del parametro σ della nostra gaussiana. È immediato rendersi conto che al diminuire della varianza, la funzione d’onda iniziale risulta sempre
più localizzata nello spazio delle configurazioni. Il caso limite è quello della
delta di Dirac che otteniamo per σ che tende a zero.
Direttamente dall’equazione (6.6) sappiamo che tanto più la particella è localizzata all’istante iniziale, tanto più lo spreading cresce durante l’evoluzione.
In figura (6.5) abbiamo utilizzato una gaussiana molto stretta che può considerarsi un’approssimazione della delta di Dirac; si può notare l’entità dello
spreading confrontando questo grafico con la gaussiana di minima indeterminazione in figura (6.3). Facciamo notare la differenza fra gli intervalli
temporali considerati (1.2 secondi nella figura (6.3) contro 0.15 secondi della
figura (6.5)).
44
Figura 6.5: Evoluzione libera di una gaussiana molto piccata.
Parametri: σin = 0.05, ε = 0.001, k = 150, x0 = 0
45
Capitolo 7
Simulazione di un oscillatore
armonico
Say not, “I have found the truth”, but rather “I have found a
truth”.
Kahlil Gibran
7.1
Descrizione del sistema
In questo capitolo simuleremo l’evoluzione dell’oscillatore armonico.
Consideriamo una particella che compie piccole oscillazioni unidimensionali.
L’energia potenziale di tale particella è uguale a mω 2 x2 /2 dove ω rappresenta
nella meccanica classica la frequenza propria delle oscillazioni. L’hamiltoniana quantistica associata a questo sistema dinamico è quindi la seguente:
Ĥ =
p̂2
1
+ mω 2 x̂2
2m 2
(7.1)
Poichè l’energia potenziale diventa infinita per x ± ∞, la particella può compiere soltanto un moto finito e, di conseguenza, tutto lo spettro energetico
dell’oscillatore sarà discreto. L’equazione di Schrödinger per il problema
considerato ha la forma
d2 ψ 2m
+ 2
dx2
~
mω 2 x2
E−
ψ=0
2
46
(7.2)
È comodo introdurre la variabile adimensionale ξ definita dalla relazione
r
mω
ξ=
x
~
Si ottiene allora l’equazione
00
ψ +
2E
2
−ξ ψ =0
~ω
Per grandi ξ si può trascurare 2E/~ω rispetto a ξ 2 . L’equazione ξ 00 = ξ 2 ψ
ha come integrali asintotici ψ = e±ξ
2 /2
(la derivazione di questa funzione dà
infatti, trascurando i termini di ordine inferiore in ξ, ψ 00 = ξ 2 ψ). Dato che
la funzione d’onda ψ deve essere finita per ξ = ±∞, nell’esponente occorre
scegliere il segno meno. In relazione a ciò, è naturale fare nell’equazione (7.2)
la sostituzione
ψ = e−ξ
2 /2
χ (ξ)
Per la funzione χ (ξ) si ottiene la seguente equazione (introduciamo la notazione 2E/~ω − 1 = 2n)
χ00 − 2ξχ0 + 2nχ = 0
(7.3)
da risolvere con la condizione che la funzione χ deve essere finita per tutte
le ξ finite, e per ξ = ±∞ essa può crescere indefinitamente, ma non più
rapidamente di una potenza finita di ξ (in modo che la funzione ψ tenda a
zero). Le soluzioni dell’equazione (7.3) corrispondenti ai diversi valori interi
positivi di n sono
χ = costante · Hn (ξ)
dove Hn (ξ) sono polinomi di grado n in ξ, detti polinomi di Hermite, dati
dalla formula
2
dn e−ξ
dξ n
Determinando la costante in modo tale che le funzioni ψn siano normalizzate,
Hn (ξ) = (−1)n eξ
2
otteniamo finalmente
ψn (x) =
mω 1/4
π~
r
mω 2
1
mω
− 2~ x
√
Hn x
e
~
2n n!
47
(7.4)
Ad esempio, la funzione d’onda dello stato fondamentale è data da
mω 1/4 mω 2
ψ0 (x) =
e− 2~ x
(7.5)
π~
e quella del primo stato eccitato
√ 2 mω 3/4 − mω x2
ψ1 (x) = 1/4
xe 2~
(7.6)
π
~
Per trovare la dinamica di questo sistema utilizziamo l’equazione del moto
di Heisenberg. Dato ÂH un operatore nella rappresentazione di Heisenberg,
l’equazione della dinamica quantistica si può scrivere nella seguente forma:
i
1 h
dÂH
(t) =
ÂH (t) , Ĥ
(7.7)
dt
ih
Applichiamo ora l’equazione (7.7) alle variabili dinamiche del nostro sistema,
ovvero a x̂ e p̂.
i~
i
dx̂ h
1 2
1
p̂
= x̂, Ĥ =
x̂, p̂ =
2p̂i~ = i~
dt
2m
2m
m
Ne risulta:
p̂
dx̂
=
dt
m
Da cui otteniamo:
p̂ (0)
sin ωt
mω
Una trattazione analoga per l’operatore momento ci conduce a:
x̂ (t) = x̂ (0) cos ωt +
p̂ (t) = −mωx̂ (0) sin ωt + p̂ (0) cos ωt
(7.8)
(7.9)
Le equazioni (7.8) e (7.9) derivate dal moto quantistico appaiono uguali alle
equazioni classiche.1 Facciamo osservare che gli operatori x̂ e p̂ oscillano
1
Questo fatto non ci stupisce più di tanto; nel 1925 P.A.M. Dirac osservò che le varie
relazioni quanto-meccaniche possono essere ottenute dalle corrispondenti relazioni classiche
semplicemente sostituendo alle parentesi di Poisson i commutatori nel modo seguente
{, } −→
[, ]
i~
Ricordiamo che le parentesi di Poisson classiche sono definite, per funzioni di q e p, da
X ∂A ∂B
∂A ∂B
{A (q, p) , B (q, p)} ≡
−
∂qs ∂ps
∂ps ∂qs
s
48
come i loro analoghi classici.
Si potrebbe pensare, guardando le equazioni (7.8) e (7.9), che anche i valori
medi degli operatori oscillino con pulsazione ω. È facile però rendersi conto
che questa supposizione è errata.
Prendiamo un autostato dell’energia, caratterizzato da un certo valore di n;
si ha che il valore medio hn|x̂ (t)|ni è nullo perchè x̂ e p̂ cambiano n in n ± 1,
e |ni è ortogonale a |n ± 1i. Per avere oscillazioni simili a quelle classiche
dobbiamo avere una sovrapposizione di autostati dell’energia come
|ψi = c0 |0i + c1 |1i
Per esempio consideriamo questa combinazione lineare di autostati
1
|ψi = √ |0i + |1i
2
(7.10)
e calcoliamone il valor medio di x̂ usando gli operatori di creazione e distruzione â† e â .
r
~
†
h0| + h1| â + â |0i + |1i
2mω
r
1
~
†
=
h0|â (t) |1i + h1|â (t) |0i
2 2mω
1
hψ|x̂|ψi =
2
Sapendo che
â (t) = â (0) e−iωt
â† (t) = â† (0) eiωt
otteniamo:
r
~
cos ωt
(7.11)
2mω
Considerazioni analoghe per p̂ ci fanno concludere che esso sarà proporzionale
hψ|x̂ (t)|ψi =
alla funzione seno.
A partire dall’equazione (7.10), moltiplicando per il bra hx| otteniamo:
1
hx|ψi = √ hx|0i + hx|1i
2
49
(7.12)
Questa è una combinazione lineare delle prime due autofunzioni dell’oscillatore armonico, definite dall’espressione (7.4) e che sono riportate nelle
equazioni (7.5) e (7.6).
Abbiamo simulato l’evoluzione temporale dei valori medi di x̂ e p̂ con il
quantum simulator ; il risultato esposto in figura (7.2) è in pieno accordo con
quanto trovato nell’equazione (7.11).
Questi stati però si sparpagliano in modo infinito al crescere del tempo. Dobbiamo quindi intraprendere un’altra strada, prendendo in considerazione gli
stati coerenti.
50
Figura 7.1: Funzione d’onda dell’equazione (7.10) nello spazio delle configurazioni.
Le funzioni tratteggiate sono la prima e la seconda autofunzione dell’oscillatore
armonico, mentre quella in viola è la sovrapposizione da noi considerata.
Figura 7.2: Riportiamo i valori medi degli operatori x̂ (in rosso) e p̂ (in blu). Essi
oscillano come i loro omologhi classici.
51
7.2
Stati coerenti
Il nostro obiettivo è costruire una sovrapposizione di autostati dell’energia in
maniera da meglio mimare l’oscillatore classico, ovvero vogliamo un pacchetto
che rimbalzi avanti e indietro senza che la sua forma si allarghi. Gli stati
coerenti fanno al caso nostro. Essi sono definiti dall’equazione agli autovalori
per l’operatore di distruzione non hermitiano â:
z∈C
â|zi = z|zi
Vediamo qual è l’espressione di queste ampiezze di probabilità. Le funzioni
d’onda cercate debbono avere la forma:
ip̄x (x − x0 )2
1
exp
−
− iϕ (t)
ψ (x, t) =
~
4 (δx)2
(2π)1/4 (δx)1/2
(7.13)
dove x̄ = x̄ (t) e p̄ = p̄ (t) = mx̄˙ (t) sono i valori medi della coordinata e della
quantità di moto. Ricordando che per l’oscillatore armonico p̄˙ = −mω 2 x, si
ottiene:
x̄¨ + ω 2 x̄ = 0
(7.14)
cioè la funzione x̄ (t) soddisfa l’equazione del moto classica. Il coefficiente
costante nell’equazione (7.13) è determinato al solito imponendo la condizione di normalizzazione; oltre a questo fattore, ψ può contenere ancora un
moltiplicatore di fase con la fase ϕ (t) dipendente dal tempo. Le incognite, la
costante δx e la funzione ϕ (t) si trovano sostituendo la (7.13) nell’equazione
d’onda
~2 ∂ 2 ψ mω 2 x2
∂ψ
+
ψ = i~
2
2m ∂x
2
∂t
Tenendo conto della (7.14), dopo la sostituzione otteniamo
2
2 2
2 2
x
mω
1
m x̄˙
x̄2
1
m
− xx̄
−
+
−
+
− ϕ̇ (t) = 0
2
~2
2~2
~
4 (δx)4
8 (δx)4 4 (δx)2
−
da cui (δx)2 = ~/2mω e quindi
ϕ̇ =
ω
m 2
x̄˙ − ω 2 x̄2 +
2~
2
ϕ=
52
1
ω
p̄x̄ + t
2~
2
Si ha in definitiva
1/4
ip̄x mω (x − x̄)2
−iωt ip̄x̄
mω
exp
−
exp
−
(7.15)
ψ (x, t) =
π~
~
2~
2
2~
Questa funzione d’onda è una gaussiana centrata attorno al valor medio
dell’operatore posizione. La cosa più importante ai fini della nostra trattazione è che questa funzione è sempre un pacchetto di minima indeterminazione, per ogni istante di tempo considerato. Considerando x̄ = 0 e p̄ = 0,
l’equazione (7.15) si riduce alla funzione d’onda dello stato fondamentale dell’oscillatore armonico.
L’energia media dell’oscillatore è data da
p̄2
mω 2 x̄2 ~ω
1
Ē =
+
+
≡ ~ω n̄ +
;
2m
2
2
2
la grandezza n̄ introdotta qui è il numero medio di quanti ~ω nello stato
considerato. Si vede che esso è completamente definito da una funzione x̄ (t)
che soddisfi l’equazione classica (7.14). Questa funzione in generale si scrive
mωx̄ + ip̄
√
= âe−iωt
2m~ω
Essa descrive il legame che intercorre fra lo stato considerato e i valori medi
della posizione e del momento. La funzione (7.15) può essere sviluppata
secondo le funzioni d’onda degli stati stazionari φn dell’oscillatore
∞
X
1
ψ=
an ψ n
ψn (x, t) = φn (x) exp −i n +
ωt
2
n=0
I coefficienti dello sviluppo si calcolano come integrali
Z +∞
an =
(ψn∗ ψ) dx
−∞
Da qui la probabilità che l’oscillatore si trovi nello stato n è
wn = |an |2 = e−n̄
n̄n
n!
(7.16)
cioè è data dalla nota distribuzione di Poisson. Abbiamo quindi una sovrapposizione infinita di tutti gli stati dell’energia, ognuno considerato con il
proprio peso.
53
Simulazione
Consideriamo come funzione d’onda iniziale il seguente stato coerente:
!
1
(x − x0 )2
i
ψ (x, 0) =
exp −
+ p0 (x − x0 )
(7.17)
2
~
(π)1/4
e valutiamone l’evoluto temporale utilizzando il quantum simulator.
I risultati trovati sono riportati in figura (7.3) e in figura (7.4). L’evoluzione
temporale degli stati coerenti è in tutto simile alla dinamica dell’oscillatore
classico. La funzione d’onda rimane localizzata; l’indeterminazione come
possiamo notare dal grafico (7.5) rimane costante nel tempo.
Figura 7.3: Evoluzione di uno stato coerente.
Parametri in riferimento all’equazione (7.17): x0 = 2.5, p0 = 0; ε = π/80, k = 320.
54
Figura 7.4: Evoluzione di uno stato coerente.
Parametri in riferimento all’equazione (7.17): x0 = 1, p0 = −2; ε = π/80, k = 320.
Figura 7.5: Andamento dell’indeterminazione dello stato coerente di figura (7.3):
è una costante.
55
7.3
Stati non coerenti
In questo capitolo simuleremo l’evoluzione temporale di stati non coerenti, il
cui spreading non è costante nel tempo.
7.3.1
Stati di forma gaussiana
Cominciamo prendendo in esame stati di forma gaussiana:
!
1
(x − x0 )2
ψ (x, 0) =
exp −
2σ 2
(π)1/4 (σ)1/2
(7.18)
Contrariamente a quanto accadeva per gli stati coerenti, le funzioni d’onda della forma (7.18) sono soggette ad uno sparpagliamento maggiore come
possiamo notare dalla figura (7.6).
(a) Distribuzione di probabilità
(b) Indeterminazione
Figura 7.6: Evoluzione temporale di uno stato gaussiano.
Parametri in riferimento all’equazione (7.18): x0 = 2.5, σ = 2; ε = π/40, k = 160.
56
7.3.2
Stati di forma rettangolare
Analizziamo uno stato di forma rettangolare:

1

√
per x0 − η ≤ x ≤ x0 + η
2η
ψ (x, 0) =

0
altrove
(7.19)
Può essere interessante un confronto fra le figure (7.6) e (7.7). L’andamento tutto sommato è il medesimo; ciò che cambia, però, sono i valori
dell’indeterminazione, molto più grandi in questo caso rispetto al profilo
gaussiano.
(a) Distribuzione di probabilità
(b) Indeterminazione
Figura 7.7: Evoluzione temporale di uno stato di forma rettangolare.
Parametri in riferimento all’equazione (7.19): x0 = 2.5, η = 1; ε = π/40, k = 160.
57
7.3.3
Stati di forma lorenziana
Consideriamo ora stati di forma lorenziana:
r
ξ 3/2
2
ψ (x, 0) =
π (x − x0 )2 + ξ 2
(7.20)
È facile verificare che questo stato è normalizzato. Osservando l’evoluzione
dello stato lorenziano, possiamo notare come essa sia molto simile a quella del
pacchetto gaussiano; ciò non ci stupisce più di tanto se pensiamo all’affinità
tra il profilo della gaussiana e quello della lorenziana.
Dando uno sguardo al grafico dell’indeterminazione, vediamo una profonda
somiglianza con l’andamento del pacchetto gaussiano.
(a) Distribuzione di probabilità
(b) Indeterminazione
Figura 7.8: Evoluzione temporale di uno stato lorenziano.
Parametri in riferimento all’equazione (7.20): x0 = 3.5, ξ = 2; ε = π/40, k = 160.
58
7.4
Onde contropropaganti: interferenza
Concludiamo questo capitolo prendendo in esame l’evoluzione temporale di
due pacchetti gaussiani contropropaganti.
La funzione d’onda iniziale quindi è una sovrapposizione di due gaussiane:
!
(x − x1 )2
1
exp −
ϕ1 (x, 0) =
(7.21)
2σ 2
(π)1/4 (σ)1/2
!
1
(x − x2 )2
ϕ2 (x, 0) =
(7.22)
exp −
2σ 2
(π)1/4 (σ)1/2
I parametri scelti per la simulazione sono stati i seguenti: σ = 0.5, x1 = 5,
x2 = −5. Il risultato ottenuto è quello di figura (7.9).
Si riconosce chiaramente un pattern di interferenza, fenomeno tipico del mondo ondulatorio. E fin qui nulla di strano. La stravaganza di questo risultato
emerge prepotentemente quando andiamo a riflettere sul significato fisico di
ciò che rappresentiamo con questo grafico, ovvero una densità di probabilità
relativa ad una particella, al suo poter essere o non essere in una determinata
posizione. La conclusione a cui si giunge è che nel mondo quantistico anche le
particelle fanno interferenza. Ad ogni particella, infatti, è associata un’onda,
secondo la relazione di De Broglie: p = ~k.
A questo punto una domanda sorge spontanea: perchè allora nel mondo
macroscopico in cui viviamo non vediamo gli oggetti interferire? In prima
istanza perchè le lunghezze d’onda associate a oggetti mascroscopici sono
piccolissime, dato che ~ ≈ 1.06 · 10−34 [J · S].
In secondo luogo perchè c’è il fenomeno della decoerenza: gli oggetti macroscopici interagiscono di continuo con l’ambiente esterno e ciò distrugge la
delicata sovrapposizione quantistica degli stati; viene quindi meno la loro
natura ondulatoria.
Questo campo è oggetto di ferventi studi poichè anche i qubit di un computer
quantistico sono soggetti all’interazione con l’ambiente esterno e ciò provoca
errori; lo scopo è di limitare al massimo questo accoppiamento e di costrui-
59
re degli appositi codici di correzione che ci permettano di risolvere questi
problemi.
Figura 7.9: Sovrapposizione di due pacchetti d’onda contropropaganti in un
potenziale armonico. È evidente il parallelismo con l’esperimento della doppia
fenditura del medico inglese Thomas Young.
60
Capitolo 8
Simulazione di una particella in
un campo uniforme
The purpose of computing is insight, not numbers.
R.W. Hamming
Models are to be used, but non to be believed.
Henri Theil
8.1
Descrizione del sistema
Consideriamo il moto di una particella in un campo esterno uniforme. Orientiamo il campo lungo l’asse x, e sia F la forza agente sulla particella nel
campo; in un campo elettrico E questa forza è uguale a F = eE, dove e è
la carica della particella. L’energia potenziale di una particella in un campo
uniforme si scrive U = −F x + cost; scegliendo la costante in modo tale che
si abbia U = 0 per x = 0, si ottiene U = −F x.
L’equazione di Schrödinger per il problema considerato ha la forma
d2 ψ 2m
+ 2 (E + F x) ψ = 0
(8.1)
dx2
~
Poichè U tende a +∞ per x → −∞, e U → −∞ per x → +∞, è a priori
evidente che i livelli energetici formano uno spettro continuo che riempie tutto
61
l’intervallo dei valori da −∞ a +∞. Tutti questi autovalori corrispondono a
un moto finito nella direzione di x = −∞ e infinito nella direzione x → +∞.
Introduciamo in sostituzione della coordinata la variabile adimensionale
1/3
2mF
E
ξ = x+
F
~2
Allora l’equazione (8.1) assume la forma
ψ 00 + ξψ = 0
(8.2)
Questa equazione non contiene più il parametro energia. Di conseguenza, ottenuta la sua soluzione che soddisfa le condizioni di finitezza, avremo l’autofunzione per valori arbitrari dell’energia. L’espressione (8.2) è un’equazione
nota in fisica-matematica; la soluzione finita per tutte le x ha la seguente
forma:
ψ (ξ) = AΦ (−ξ)
dove
1
Φ (ξ) = √
π
Z
∞
cos
0
u2
+ uξ du
3
(8.3)
(8.4)
è la cosiddetta funzione d’Airy, ed A è un parametro di normalizzazione
definito da:
A=
(2m)1/3
π 1/2 F 1/3 ~2/3
Figura 8.1: Funzione di Airy.
62
Per trovare la dinamica del sistema utilizziamo al solito le equazioni del
moto di Heisenberg. L’hamiltoniana associata al sistema da noi considerato
è la seguente:
p̂2
+ αx̂
(8.5)
2m
dove α è un parametro reale. Il potenziale considerato è quindi di tipo lineare.
Ĥ =
Scriviamo ora l’evoluzione dell’operatore di Heisenberg p̂:
i
dp̂ h
i~ = p̂, Ĥ = [p̂, αx̂] = (−i~) α
dt
dp̂
⇒
= −α
dt
e per x̂:
i p̂2 i~ dx̂ h
i~
= x̂, Ĥ = x̂,
=
p̂
dt
2m
m
dx̂
p̂
⇒
=
dt
m
Combinando le due equazioni differenziali otteniamo:
d2 x̂
dp̂ 1
α
=
=−
2
dt
dt m
m
(8.6)
che descrive il moto di una particella accelerata.
Integrando due volte e utilizzando opportune costanti di integrazione perveniamo a
x̂ (t) = x̂ (0) + p̂ (0) t − (α/2m) t2
(8.7)
p̂ (t) = p̂ (0) − αt
(8.8)
che sono le medesime dell’evoluzione classica, facilmente deducibili utilizzando le equazioni di Hamilton. Riconduciamo ora le nostre equazioni operatoriali a qualcosa di osservabile considerandone i valori medi; per il teorema di
Ehrenfest possiamo scrivere
d2
m 2 hx̂i = −h∇V̂ (x)i = −α
dt
(8.9)
da cui capiamo che i valori medi seguono esattamente la stessa legge del caso
classico.
63
8.2
Simulazione
Prendiamo in esame al solito uno stato di forma gaussiana
!
1
(x − x0 )2
ψ (x, 0) =
exp −
2σ 2
(π)1/4 (σ)1/2
(8.10)
e simuliamo la sua evoluzione temporale sottoposto al potenziale lineare V =
αx. In figura (8.2) riportiamo il risultato della simulazione.
Figura 8.2: Evoluzione di una particella in un campo uniforme.
Parametri considerati: x0 = −2.5, σ = 0.5; α = −5; ε = 0.01, k = 120.
64
Analizziamo i dati ottenuti. Innanzitutto, si nota immediatamente che
il valor medio della posizione cresce in maniera quadratica, cosa che già ci
aspettavamo dall’equazione (8.9).
In figura (8.3) abbiamo riportato i grafici dei valori di aspettazione di x̂ e p̂
nello stato da noi considerato. Ovviamente l’andamento del valor medio di
p̂ è lineare nel tempo.
(a) x̂ medio
(b) p̂ medio
Figura 8.3: Evoluzione dei valori medi degli operatori x̂ e p̂ ottenuta con il
quantum simulator.
Per quanto riguada lo sparpagliamento della funzione d’onda, il risultato
che troveremo è per certi versi sorprendente. In virtù del teorema di Ehrenfest
si ha:
d
d
d
(∆p)2 = hp2 i − 2hpi hpi = −2αhpi + 2αhpi = 0
dt
dt
dt
(8.11)
risultato questo che essendo indipendente da α, coincide con il caso della particella libera (α = 0). Un analogo discorso vale per l’operatore x̂ e
quindi possiamo concludere che lo spreading della funzione d’onda associato alla particella accelerata coincide con quello della particella libera. In
figura (8.4) riportiamo i risultati ottenuti dalla simulazione; i due spreading
effettivamente coincidono.
65
(a) Potenziale lineare
(b) Evoluzione libera
(c) Indeterminazione con potenziale lineare
(d) Indeterminazione in evoluzione libera
Figura 8.4: Confronto fra lo spreading di una particella sottoposta ad un
potenziale lineare ed un’altra in evoluzione libera. I due sparpagliamenti sono
identici.
66
Capitolo 9
Simulazione di una particella
sottoposta a buche e gradini di
potenziale
Errors, like straws, upon the surface flow; He who would
search for pearls must dive below.
John Dryden
We are all in the gutter, but some of us are looking at
the stars.
Oscar Wilde
9.1
Barriera di potenziale
In questa sezione descriveremo il moto di una particella sottoposta ad un
potenziale unidimensionale di tipo barriera e ne simuleremo l’evoluzione
con il quantum simulator. Sarà interessante notare le differenze rispetto
al comportamento previsto dalla meccanica classica.
67
9.1.1
Descrizione del sistema
Cominciamo questo capitolo dedicato ai potenziali discontinui prendendo
in considerazione la barriera di potenziale. La funzione da analizzare è la
seguente:
U (x) =

0
x≤0
U
x>0
0
(9.1)
dove U0 è un parametro reale positivo.
Il nostro obiettivo è duplice: da un lato determinare la natura delle soluzioni
Figura 9.1: Barriera di potenziale.
dell’equazione di Schrödinger agli stati stazionari, dall’altro calcolare i coefficienti di riflessione e trasmissione.
Nella regione I l’equazione stazionaria di Schrödinger è
−
~2 d2
ψI (x) = EψI (x)
2m dx2
mentre nella regione II si ha
−
~2 d2
ψII (x) = (E − U0 ) ψII (x)
2m dx2
Occorre ora distinguere i due casi: (a) E > U0 e (b) E < U0 .
68
Caso (a)
Consideriamo dapprima E > U0 .
La soluzione dell’equazione di Schrödinger nelle due regioni è
ψI (x) = Aeikx + Be−ikx
(9.2)
ψII (x) = Ceiqx + De−iqx
dove
2mE
>0
~2
2m (E − U0 )
q2 =
>0
~2
k2 =
Supponendo la particella proveniente da x = −∞ si può porre D = 0.
Imponendo poi la condizione di continuità della funzione d’onda e della sua
derivata prima in x = 0 si ottiene un sistema di due equazioni che permettono
di esprimere B e C in funzione di A (che si può eventualmente utilizzare per
normalizzare la funzione d’onda):
A + B =C
q
A−B = C
k
La soluzione del sistema è
2k
k+q
k−q
B =A
k+q
C =A
Piuttosto che usare la costante A per normalizzare la funzione d’onda è
istruttivo calcolare i coefficienti di riflessione e trasmissione definiti come
R=
jr
ji
T =
jt
ji
(9.3)
dove ji , jr e jt sono le densità di corrente di probabilità relative all’onda
incidente, all’onda riflessa ed a quella trasmessa, calcolati per mezzo della
formula
i~
j (x) = −
2m
dψ ∗
∗ dψ
ψ
−ψ
dx
dx
69
R e T rappresentano fisicamente la probabilità che una particella con energia
E > U0 venga riflessa o trasmessa dal gradino di potenziale; queste due
quantità quindi devono soddisfare la condizione R + T = 1.
Ponendo
ψr (x) = Be−ikx
ψi (x) = Aeikx
ψt (x) = Ceiqx
nell’equazione (9.3) si ottiene:
ji =
~k
|A|2
m
jr =
~k
|B|2
m
jt =
~q
|C|2
m
e dunque troviamo il coefficiente di trasmissione
2
q C 4kq
T = =
k A
(k + q)2
(9.4)
e di riflessione
2
B (k − q)2
R = =
A
(k + q)2
da cui è immediato verificare che R + T = 1.
(9.5)
Si noti che, nel limite E → ∞, E − U0 ' E. Ne segue che
q2 =
2mE
2m (E − U0 )
'
= k2
2
2
~
~
ovvero, essendo q ' k, R = 0.
Caso (b)
Veniamo ora al caso E < U0 .
La soluzione dell’equazione di Schrödinger nelle due regioni è ora
ψI (x) = Aeikx + Be−ikx
ψII (x) = Ce−qx + Deqx
dove
2mE
>0
~2
2m (U0 − E)
q2 =
>0
~2
k2 =
70
(9.6)
La costante D va posta uguale a zero perchè altrimenti ψII non sarebbe
limitata per x → ∞ e dunque risulterebbe priva di significato fisico. Confrontando le equazioni (9.2) e (9.6) è chiaro che le formule relative al caso (b)
si possono ottenere dalle formule del caso (a) con la sostituzione q → iq. In
particolare, il sistema che si ottiene imponendo la condizione di continuità
della funzione d’onda e della sua derivata prima in x = 0 ha come soluzione
2k
k + iq
k − iq
B=A
k + iq
C=A
Infine, il coefficiente di riflessione è
2
B k − iq k + iq
=1
R = =
A
k + iq k − iq
(9.7)
dunque T = 0, che significa che la particella viene riflessa con probabilità 1.
D’altra parte esiste una densità di probabilità ρ (x) non nulla di trovare la
particella nella regione II :
ρ (x > 0) = |ψII (x)|2 = |A|2
4k 2 −2qx
e
k2 + q2
(9.8)
Tale densità di probabilità è rapidamente decrescente al crescere di x e si
può comprendere fisicamente grazie al principio di Heisenberg. Infatti, in un
piccolo intorno dell’origine, non è possibile misurare con precisione infinita
la posizione della particella, che peraltro risulta avere una certa indeterminazione. Tale indeterminazione è strettamente collegata al valore non nullo
di ρ (x) a destra dell’origine. Se la posizione della particella fosse localizzata
in un punto, il momento lineare della particella sarebbe infinito.
La penetrazione della particella nella barriera di potenziale per E < U0 può
essere visualizzata secondo l’analogia ottico-meccanica facendo corrispondere
al potenziale l’indice di rifrazione di un mezzo nel quale si disperde un’onda
elettromagnetica.
71
9.1.2
Simulazione
Prendiamo come funzione d’onda iniziale la seguente gaussiana:
!
1
(x − x0 )2
i
ψ (x, 0) =
exp −
+ p0 (x − x0 )
2σ 2
~
(π)1/4 (σ)1/2
(9.9)
e simuliamo la sua evoluzione se sottoposta ad una barriera di potenziale

U0 x < −a
U (x) =
(9.10)
0
altrove
I parametri scelti per la simulazione sono stati i seguenti: σ = 0.7, a =
−2.625, p0 = −10. Abbiamo utilizzato n = 6 qubit, uno step temporale
molto piccolo (ε = 0.005) ed eseguito k = 120 iterazioni. Sono state effettuate varie simulazioni, variando di volta in volta l’altezza della barriera,
cioè il parametro U0 . I risultati sono esposti in figura (9.2); in rosso abbiamo
indicato la barriera di potenziale.
Proponiamo ora un confronto fra il moto classico e quello quantistico. Per
E < U0 una particella classica proveniente da −∞ con velocità costante rimbalza elasticamente contro la barriera di potenziale in x = 0, inverte il suo
moto e ritorna verso −∞ con la medesima velocità (in modulo). In meccanica quantistica, invece, c’è una probabilità non nulla che la particella superi la
barriera, ovvero penetri nella regione classicamente proibita (ciò è evidente
nella figura (9.2(f)).
Nell’ipotesi E > U0 invece, la particella classica quando raggiunge la barriera
di potenziale abbassa istantaneamente la sua velocità e si muove, con la nuova velocità, verso +∞. Nel mondo quantistico, di contro, c’è una probabilità
non nulla che la particella venga riflessa (vedi le figure 9.2 (a)(b)(c)(d)(e)).
72
(a) U0 = 10
(b) U0 = 20
(c) U0 = 30
(d) U0 = 40
(e) U0 = 50
(f) U0 = 70
Figura 9.2: Particella sottoposta ad una barriera di potenziale (al variare di U0 ).
73
9.2
Gradino di potenziale
Prendiamo ora in considerazione una particella sottoposta ad un potenziale
a gradino. La trattazione è molto simile a quella della sezione precedente.
9.2.1
Descrizione del sistema
Il potenziale da studiare è il seguente:

U0
U (x) =
0
0<x<a
altrove
dove U0 è un parametro reale positivo.
Figura 9.3: Gradino di potenziale.
Nella regione I l’equazione stazionaria di Schrödinger è
−
~2 d2
ψI (x) = EψI (x)
2m dx2
nella regione II si ha
−
~2 d2
ψII (x) = (E − U0 ) ψII (x)
2m dx2
mentre nella regione III
−
~2 d2
ψIII (x) = EψIII (x)
2m dx2
Occorre ora distinguere i due casi: (a) E > U0 e (b) E < U0 .
74
(9.11)
Caso (a)
La soluzione dell’equazione di Schrödinger nelle tre regioni è
ψI (x) = Aeikx + Be−ikx
ψII (x) = Ceiqx + De−iqx
(9.12)
ψIII (x) = Eeikx + F e−ikx
dove
2mE
>0
~2
2m (E − U0 )
>0
q2 =
~2
k2 =
Supponendo la particella proveniente da x = −∞ si può porre F = 0. Imponendo poi la condizione di continuità della funzione d’onda e della sua
derivata prima in x = 0 si ottiene un sistema di quattro equazioni che permettono di esprimere B, C, D ed E in funzione di A (che si può eventualmente
utilizzare per normalizzare la funzione d’onda):
A + B =C
q
A − B = (C − D)
k
iqa
−iqa
Ce + De
=Eeika
k
Ceiqa − De−iqa = Eeika
q
Scrivere la soluzione generale del sistema non è particolarmente istruttivo.
Più interessante è il calcolo dei coefficienti di riflessione e trasmissione relativi
al potenziale in esame. Analogamente a quanto già visto con la barriera di
potenziale, ponendo
ψi (x) = Aeikx
ψr (x) = Be−ikx
ψt (x) = Eeiqx
nell’equazione (9.3) si ottiene:
ji =
~k
|A|2
m
jr =
~k
|B|2
m
75
jt =
~q
|E|2
m
e dunque
2
E T = A
2
B R = A
Procediamo ora al calcolo di T esprimendo A in funzione di E. Sommando
le prime due equazioni del sistema si ottiene
D k−q
C k+q
+
A=
2
k
2
k
(9.13)
D’altra parte, sommando e sottraendo fra di loro le ultime due equazioni del
medesimo sistema si trova
E ia(k−q) k + q
C= e
2
q
E ia(k+q) k − q
D=− e
2
q
Sostituendo in (9.13) si giunge a
E ika e
(k + q)2 e−iaq − (k − q)2 eiaq
4kq
E ika e
2kq cos (aq) − i k 2 + q 2 sin (aq)
=
2kq
A=
(9.14)
Dunque
T =
4k 2 q 2
4k 2 q 2 + (k 2 − q 2 )2 sin2 (aq)
e
2
sin2 (aq) (k 2 − q 2 )
R=1−T =
4k 2 q 2 + (k 2 + q 2 )2 sin2 (aq)
Se aq = nπ (n = 1, 2 . . .) R = 0 e T = 1, che implica trasparenza assoluta
della barriera. Tale fenomeno si chiama effetto Ramsauer-Townsend.
Caso (b)
La soluzione dell’equazione di Schrödinger nelle tre regioni è
ψI (x) = Aeikx + Be−ikx
ψII (x) = Ce−qx + Deqx
ψIII (x) = Eeikx + F e−ikx
76
(9.15)
dove
2mE
>0
~2
2m (U0 − E)
q2 =
>0
~2
k2 =
Come sempre la costante F va posta uguale a zero poichè supponiamo l’onda
incidente da x = −∞. Confrontando le equazioni (9.12) e (9.15) è chiaro che,
nel caso in E < U0 , la relazione che lega E ad A si può ottenere direttamente
dall’equazione (9.14) con la sostituzione q → iq. Poichè per effetto di questo
cambio
cos (aq) → cosh (aq)
sin (aq) → i sinh (aq)
il risultato è:
A=
E ika e
2kq cosh (aq) − i k 2 − q 2 sinh (aq)
2kq
Dunque
4k 2 q 2
T =
4k 2 q 2 + (k 2 + q 2 )2 sinh2 (aq)
e
2
sinh2 (aq) (k 2 + q 2 )
R=1−T =
4k 2 q 2 + (k 2 + q 2 )2 sinh2 (aq)
Il fatto che T sia diverso da zero implica una probabilità non nulla di passaggio attraverso la barriera anche nel caso E < U0 . Tale fenomeno si chiama effetto tunnel. Per concludere osserviamo che la probabilità di trovare,
per effetto tunnel, la particella al di là della barriera è esponenzialmente
decrescente nel limite di barriere alte e larghe (aq → ∞). Infatti in tale
limite
T ∼
16k 2 q 2 −2aq
e
(k 2 + q 2 )2
77
9.2.2
Simulazione
Consideriamo stati iniziali di forma gaussiana:
ψ (x, 0) =
1
(π)1/4 (σ)1/2
(x − x0 )2
i
exp −
p
(x
−
x
)
+
0
0
2σ 2
~
!
(9.16)
e simuliamo la loro evoluzione temporale se sottoposti al potenziale a gradino

U0 −a < x < a
U (x) =
(9.17)
0
altrove
I parametri scelti per la simulazione sono stati i seguenti: σ = 0.7, a = 0.875,
p0 = −10. Abbiamo utilizzato n = 6 qubit, uno step temporale molto piccolo
(ε = 0.005) ed eseguito k = 120 iterazioni. Sono state effettuate varie simulazioni, variando di volta in volta l’altezza del gradino di potenziale, cioè il
parametro U0 . I risultati sono esposti in figura (9.4); in rosso abbiamo indicato l’ubicazione del gradino di potenziale per una più facile interpretazione
del comportamento del sistema.
Può essere interessante ora comparare il moto quantistico da noi simulato
con quello di una particella classica con la medesima energia e proveniente da
x = −∞. La differenza più importante si ha per E < U0 . La particella classica rimbalza contro il gradino di potenziale; non è possibile penetrare nella
barriera. In meccanica quantistica invece abbiamo una probabilità non nulla
di passaggio attraverso la barriera anche nel caso E < U0 . Tale fenomeno si
chiama effetto tunnel. Possiamo vedere molto bene questa peculiarità della
meccanica quantistica volgendo la sguardo alla figura (9.4 (f)).
Quando E > U0 , la particella classica è rallentata nella zona dove è presente
il gradino di potenziale, ma comunque lo attraversa e continua il suo moto verso +∞. Il pacchetto quantistico invece è quasi sempre parzialmente
riflesso (tranne in casi particolari già visti nella sezione precedente). Possiamo apprezzare questo fatto osservando le figure (9.4 (a)(b)(c)(d)(e)). Il
limite classico ovviamente si ottiene quando l’energia del pacchetto incidente
è molto maggiore dell’altezza della barriera.
78
(a) U0 = 10
(b) U0 = 20
(c) U0 = 30
(d) U0 = 40
(e) U0 = 50
(f) U0 = 60
Figura 9.4: Particella sottoposta ad un potenziale a gradino (al variare di U0 ).
79
Prendiamo ora in esame un potenziale a gradino con un profilo stavolta
gaussiano. L’espressione analitica è
(x − x0 )2
U (x) = U0 exp −
2σ 2
!
(9.18)
dove abbiamo settato U0 = 60 e x0 = 1.
Considerando che l’energia della particella incidente è E ' 50, siamo nelle
condizioni in cui E < U0 . Ora andiamo a simulare l’evoluzione di questo
sistema al variare della larghezza del gradino di potenziale (cioè il parametro
σ dell’equazione (9.18)). L’idea è quella di investigare l’effetto tunnel e la sua
dipendenza con le dimensioni lineari del potenziale. I risultati sono esposti
in figura (9.5).
Osservando questi grafici possiamo notare come l’effetto tunnel aumenti al
diminuire della larghezza del gradino di potenziale (ricordiamo che U0 è
un parametro fissato). Il caso limite, in cui il potenziale è puntiforme, è
presentato nella sezione successiva.
80
(a) σ = 0.5
(b) σ = 0.3
(c) σ = 0.16
(d) σ = 0.1
(e) σ = 0.08
(f) σ = 0.05
Figura 9.5: Particella sottoposta ad un gradino di potenziale gaussiano (al variare
della larghezza σ della gaussiana).
81
9.3
Potenziale deltiforme
Consideriamo ora un potenziale un po’ particolare: la delta di Dirac. La
simulazione quantistica di un sistema sottoposto al suddetto potenziale ci
darà dei risultati sorprendenti.
9.3.1
Descrizione del sistema
Il coefficiente di trasmissione si può ricavare da quello ottenuto considerando
il gradino di potenziale considerando il limite con a → 0:
4k 2 q 2
=1
a→0 4k 2 q 2 + (k 2 + q 2 )2 sinh (aq)
T = lim
(9.19)
Si ha quindi trasparenza totale della barriera. Incredibile ma vero.
9.3.2
Simulazione
Per simulare la delta di Dirac in un sistema discreto dobbiamo compiere
ovviamente delle approssimazioni; la nostra scelta è di considerare una gaussiana molto piccata, cioè con una varianza molto piccola ed un’ampiezza
molto grande. In altri termini:
(x − x0 )2
ψ (x, 0) = U0 exp −
2σ 2
!
(9.20)
con σ = 5 · 10−4 e U0 = 106 . Una particella sottoposta a questo tipo di
potenziale non sente la barriera; si ha trasmissione totale. Il risultato trovato
è riportato in figura (9.6). Un identico risultato si trova ponendo più delte di
Dirac in varie posizioni. Questa configurazione approssima bene il potenziale
all’interno di un metallo.
82
Figura 9.6: Evoluzione di una particella sottoposta ad un potenziale deltiforme
in x = 0. La particella non “sente”la barriera.
83
Capitolo 10
Simulazione di una particella
sottoposta a potenziali
anarmonici
Computers are good at following instructions, but not at
reading your mind.
Donald Knuth
If you can’t explain it simply, you don’t understand it
well enough.
Albert Einstein
10.1
Potenziale anarmonico cubico
In questa sezione simuleremo l’evoluzione temporale di un sistema sottoposto
al seguente potenziale unidimensionale:
1
 mω 2 x2
V (x) = 2
αx3
x>0
(10.1)
x≤0
Abbiamo quindi sia un potenziale armonico che un potenziale cubico.
La nostra funzione d’onda iniziale è uno stato coerente dell’oscillatore ar84
monico (come dimostrato nel capitolo 7):
ψ (x, 0) =
1
(π)1/4
i
(x − x0 )2
+ p0 (x − x0 )
exp −
2
~
!
(10.2)
È importante però far notare che gli stati di questa forma mantengono la
minima indeterminazione solo se sottoposti ad un potenziale armonico. Nel
nostro caso, invece, vi è anche un potenziale cubico; ciò significa che la funzione d’onda subirà una deformazione ed uno spreading rilevante durante
l’evoluzione.
Simulazione
In riferimento all’equazione (10.2), i parametri da noi considerati sono stati
x0 = 2.5 e p0 = 0. Abbiamo posto come al solito ~ = m = ω = 1 e utilizzato
n = 6 qubit. Per quanto riguarda il parametro α del potenziale cubico, sono
state realizzate diverse simulazioni considerandone valori differenti. In figura
(10.1) riportiamo l’evoluzione della funzione d’onda e l’indeterminazione dei
due risultati più significativi.
Il risultato più interessante dal punto di vista della dinamica quantistica è la
perdita di coerenza del pacchetto d’onda già dopo poche oscillazioni, a causa
del potenziale cubico. Un altro fatto degno di nota è la deformazione della
funzione d’onda; se questo fenomeno si intuisce già nella figura (10.1(a)),
nel grafico (10.1(c)) ne abbiamo una prova evidente. Rispetto al risultato
ottenuto con il solo potenziale armonico, infatti, la funzione d’onda perde la
sua simmetria rispetto all’asse orizzontale; ciò è dovuto al fatto che per x
negativi il potenziale è cubico, non armonico.
85
(a) Funzione d’onda (α = −0.1)
(b) Indeterminazione (α = −0.1)
(c) Funzione d’onda (α = −0.4)
(d) Indeterminazione (α = −0.4)
Figura 10.1: Evoluzione di una particella sottoposta al potenziale anarmonico
dell’equazione (10.1).
86
10.2
Potenziale armonico con perturbazione
quartica
Prendiamo ora in esame il seguente potenziale:
1
V (x) = mω 2 x2 + βx4
2
(10.3)
e simuliamone l’evoluzione. La funzione d’onda iniziale e i parametri considerati sono i medesimi del caso precedente. In figura (10.2) riportiamo i
risultati ottenuti per qualche valore del parametro β.
(a) β = 0.01
(b) β = 0.02
(c) β = 0.04
(d) β = 0.1
Figura 10.2: Evoluzione di una particella sottoposta al potenziale armonico con
perturbazione quartica dell’equazione (10.3).
87
Il nostro sistema è molto sensibile alla perturbazione quartica; basta infatti un valore molto piccolo di β (peso del potenziale quartico) per far sı̀ che
la coerenza venga del tutto distrutta già dopo una sola oscillazione. Ciò è ancora più chiaro volgendo lo sguardo ai grafici dell’indeterminazione riportati
in figura (10.3). In particolare, il grafico (10.3(d)) ci mostra come l’indeterminazione cresca fino a raggiungere la saturazione numerica del sistema:
dopo poche iterazione la particella può stare dappertutto.
(a) β = 0.01
(b) β = 0.02
(c) β = 0.04
(d) β = 0.1
Figura 10.3: Evoluzione dell’indeterminazione di una particella sottoposta al
potenziale armonico con perturbazione quartica dell’equazione (10.3). Facciamo
notare la diversità nella scala dell’asse delle ordinate nei diversi grafici.
Nel grafico (d) viene raggiunta la saturazione numerica del sistema in un tempo
pari a circa 6s; ovviamente i dati oltre quella soglia non hanno più significato
fisico perchè la saturazione è di tipo numerico cioè è dovuta al box di simulazione
considerato.
88
Capitolo 11
Conclusioni
A great discovery solves a great problem but there is a
grain of discovery in the solution of any problem.
G. Polya
In questo lavoro abbiamo dimostrato che un piccolo registro quantistico
da 6-10 qubit è sufficiente a realizzare un simulatore quantistico in grado di
risolvere problemi elementari di meccanica quantistica. Per far ciò è stato
scritto un programma in Fortran che ci permettesse di studiare il comportamente del sistema fisico di volta in volta considerato.
Il simulatore quantistico sviluppato in questa tesi può essere un utile strumento didattico poichè ci permette di conoscere l’evoluzione del problema
che ci interessa risolvere, fornendoci un’indicazione precisa sulla natura delle
soluzioni. Possiamo quindi controllare, per esempio, i risultati a cui siamo
giunti, risolvendo con carta e penna il problema. Molte volte, però, è molto
difficile pervenire ad una risoluzione analitica del problema considerato; in
questi casi possiamo utilizzare il quantum simulator per capire l’evoluzione
del sistema.
Un possibile sviluppo del quantum simulator è la sua generalizzazione a tre
dimensioni, in modo da poter considerare potenziali V (x, y, z) dipendenti
dalle tre variabili spaziali. A questo punto, i risultati ottenuti saranno esposti in tre grafici distinti, in cui compaiono rispettivamente ψ (x, t), ψ (y, t) e
89
ψ (z, t). Molto interessante sarebbe poi passare in coordinate sferiche, con
una funzione d’onda ψ (r, ϑ, φ, t), provando magari a simulare problemi di
scattering da potenziali arbitrariamente scelti.
Considerando poi il moto di una particella sottoposta ad una barriera di
potenziale, sarebbe interessante trovare un metodo per determinare quantitativamente il coefficiente di riflessione e di trasmissione, in modo da poterli
confrontare con quelli trovati analiticamente.
90
Appendice - Codice sorgente
Software and cathedrals are much the same - first we build
them, then we pray.
Anonymous
Programma in Fortran
!-----------------------------------------------------------------------------! Simulazione di una particella quantistica sottoposta ad un potenziale V(x)
! Autore: Ziletti Angelo
! Università Cattolica del Sacro Cuore (Brescia)
! Dicembre 2008
!-----------------------------------------------------------------------------PROGRAM Quantum_Simulator
IMPLICIT NONE
REAL, PARAMETER :: Pi = 3.1415927
!pi greco
REAL, PARAMETER :: x0 = 2.5
REAL, PARAMETER :: p0 = 0
REAL, PARAMETER :: s = 1
!sigma
REAL, PARAMETER :: d = 5
!intervallo in x del tipo [-d,d]
REAL, PARAMETER :: e = Pi/80
!step discretizzazione temporale
REAL, PARAMETER :: h = 1
!h tagliato
REAL, PARAMETER :: m = 1
!massa
INTEGER, PARAMETER :: n = 8
!numero di qubits
INTEGER, PARAMETER :: c = 160
!numero di cicli temporali
INTEGER :: i,j,k,q,u,t
REAL :: dx,NC,Xm,Pm,X2m,P2m,Xind,Pind,indstep
COMPLEX :: uim
!unità immaginaria
REAL,DIMENSION(1:2**n) :: Xj
!coordinate spaziali
REAL,DIMENSION(1:2**n) :: Pj
!momenti
REAL,DIMENSION(1:2**n) :: Vj
!potenziale
COMPLEX,DIMENSION(1:2**n) :: Ybn
!step iniziale
COMPLEX,DIMENSION(1:c,1:2**n) :: Y
!array coefficienti
91
COMPLEX,DIMENSION(1:2**n) :: Yor
REAL,DIMENSION(1:2**(n+1)) :: Yror
REAL,DIMENSION(1:c,1:2**n) :: Y2
REAL,DIMENSION(1:c,1:2**(n+1)) :: R
REAL,DIMENSION(1:c) :: IND
!array processato
!array processato reale
!array probabilità
!probabilità e stato
!indeterminazione
!inizializzazione variabili
Xj = 0.0 ; Pj = 0.0 ; Vj = 0.0
Ybn = 0.0 ; Y = 0.0 ; Y2 = 0.0
Yor = 0.0 ; Yror = 0.0 ; R = 0.0
NC = 0 ; q = 0 ; u = 0 ; t = 0
Xm = 0 ; X2m = 0 ; Xind = 0
Pm = 0 ; P2m = 0 ; Pind = 0
indstep = 0 ; IND = 0.0
uim = CMPLX(0,1) !unità immaginaria
!step discretizzazione spaziale
dx = (2*d)/(2**n)
!discretizzazione dell’intervallo spaziale
DO j=1,2**n
Xj(j) = -d + (j-1)*dx
END DO
!calcolo della funzione d’onda discretizzata
DO j=1,2**n
Ybn(j) = (1/(sqrt(sqrt(Pi)*s)))*exp(-((Xj(j)-x0)**2)/(2*(s**2))+ (uim/h)*p0*(Xj(j)-x0))
END DO
!ricerca della costante di normalizzazione
DO j=1,2**n
NC = NC + ABS(Ybn(j))**2
END DO
!normalizzazione
DO k=1,2**n
Y(1,k) = (1/SQRT(NC))*(Ybn(k))
END DO
!costruzione dell’array dei momenti
DO k=1,2**(n-1)+1
Pj(k) = (2*Pi*(k-1))/((2**n)*dx)
END DO
DO k=2**(n-1)+1,2**n
Pj(k) = (2*Pi*(k-1-2**n))/((2**n)*dx)
END DO
!costruzione dell’array del potenziale
DO j=1,2**n
92
Vj(j) = ((Xj(j))**2)/2
END DO
!-----------------------------!
evoluzione temporale
!-----------------------------DO t=1,c-1
Xm = 0 !inizializzo il valore medio di x
X2m = 0 !inizializzo il valore medio di x^2
Xind = 0 !inizializzo l’indeterminazione in x
Pm = 0 !inizializzo il valore medio di p
P2m = 0 !inizializzo il valore medio di p^2
Pind = 0 !inizializzo l’indeterminazione in p
indstep = 0
DO i=1,2**n
Yor(i) = Y(t,i) !estraggo dalla matrice l’array dell’evoluzione precedente
END DO
!-------------------------------------------------------! calcolo l’indeterminazione nelle X
!-------------------------------------------------------!valor medio x
DO i=1,2**n
Xm = Xm + (ABS(Yor(i))**2)*Xj(i)
END DO
!valor medio x^2
DO i=1,2**n
X2m = X2m + (ABS(Yor(i))**2)*(Xj(i)**2)
END DO
!indeterminazione in x
Xind = sqrt(X2m - (Xm**2))
!trasformo l’array complesso in reale
u = 1
DO i=1,2**n
Yror(u) = DBLE(Yor(i))
Yror(u+1) = AIMAG(Yor(i))
u = u+2
END DO
q = (size(Yror))/2 !dimensione array(argomento della chiamata)
93
CALL four1(Yror,q,1) !Fourier Transform
DO i=1,2**(n+1)
Yror(i) = (Yror(i))/(SQRT(REAL(2**n))) !coefficiente di normalizzazione
END DO
!devo ritrasformare l’array reale in complesso
u = 1
DO i=1,2**n
Yor(i) = CMPLX(Yror(u),Yror(u+1))
u = u+2
END DO
!-------------------------------------------------------! calcolo l’indeterminazione nelle P
!-------------------------------------------------------!valor medio p
DO i=1,2**n
Pm = Pm + (ABS(Yor(i))**2)*Pj(i)
END DO
!valor medio p^2
DO i=1,2**n
P2m = P2m + (ABS(Yor(i))**2)*(Pj(i)**2)
END DO
!indeterminazione in p
Pind = sqrt(P2m - (Pm**2))
!indeterminazione totale
indstep = Xind*Pind
IND(t) = indstep !indeterminazione
!------------------------------------------------------------------!
applico operatore exp(-i(p^2)/2m) --> sono nella base dei Pj
!------------------------------------------------------------------DO j=1,2**n
Yor(j) = Yor(j)*exp((-CMPLX(uim)*(Pj(j)**2)*e)/(h*2*m))
END DO
!ritrasformo l’array complesso in reale
u = 1
DO i=1,2**n
Yror(u) = DBLE(Yor(i))
Yror(u+1) = AIMAG(Yor(i))
u = u+2
94
END DO
CALL four1(Yror,q,-1) !Inverse Fourier Transform
DO i=1,2**(n+1)
Yror(i) = (Yror(i))/(SQRT(REAL(2**n))) !coefficiente di normalizzazione
END DO
!devo ritrasformare l’array reale in complesso
u = 1
DO i=1,2**n
Yor(i) = CMPLX(Yror(u),Yror(u+1))
u = u+2
END DO
!-------------------------------------------------------! applico l’operatore V(x) --> sono nella base degli Xj
!-------------------------------------------------------DO j=1,2**n
Yor(j) = Yor(j)*exp(-CMPLX(uim)*(Vj(j))*e/h)
END DO
!ora scrivo nell’array dei coefficienti
DO i=1,2**n
Y(t+1,i) = Yor(i)
END DO
IF(t==c-1) THEN !calcola l’indeterminazione dello stato finale
Xm = 0 !inizializzo il valore medio di x
X2m = 0 !inizializzo il valore medio di x^2
Xind = 0 !inizializzo l’indeterminazione in x
Pm = 0 !inizializzo il valore medio di p
P2m = 0 !inizializzo il valore medio di p^2
Pind = 0 !inizializzo l’indeterminazione in p
indstep = 0
!-------------------------------------------------------! calcolo l’indeterminazione nelle X
!-------------------------------------------------------!valor medio x
DO i=1,2**n
Xm = Xm + (ABS(Yor(i))**2)*Xj(i)
END DO
!valor medio x^2
95
DO i=1,2**n
X2m = X2m + (ABS(Yor(i))**2)*(Xj(i)**2)
END DO
!indeterminazione in x
Xind = sqrt(X2m - (Xm**2))
!trasformo l’array complesso in reale
u = 1
DO i=1,2**n
Yror(u) = DBLE(Yor(i))
Yror(u+1) = AIMAG(Yor(i))
u = u+2
END DO
q = (size(Yror))/2 !dimensione array(argomento della chiamata)
CALL four1(Yror,q,1) !Fourier Transform
DO i=1,2**(n+1)
Yror(i) = (Yror(i))/(SQRT(REAL(2**n))) !coefficiente di normalizzazione
END DO
!devo ritrasformare l’array reale in complesso
u = 1
DO i=1,2**n
Yor(i) = CMPLX(Yror(u),Yror(u+1))
u = u+2
END DO
!-------------------------------------------------------! calcolo l’indeterminazione nelle P
!-------------------------------------------------------!valor medio p
DO i=1,2**n
Pm = Pm + (ABS(Yor(i))**2)*Pj(i)
END DO
!valor medio p^2
DO i=1,2**n
P2m = P2m + (ABS(Yor(i))**2)*(Pj(i)**2)
END DO
!indeterminazione in p
Pind = sqrt(P2m - (Pm**2))
!indeterminazione totale
indstep = Xind*Pind
96
!indeterminazione
IND(c) = indstep
END IF
END DO
!costruisco l’array delle probabilità
DO i=1,c
DO j=1,2**n
Y2(i,j) = ABS(CMPLX(Y(i,j)))**2
END DO
END DO
!array dei risultati(prob e stato, prob e stato...)
DO i=1,c
u = 1
DO j=1,2**n
R(i,u) = Y2(i,j)
R(i,u+1) = Xj(j)
u = u+2
END DO
END DO
!report - esporto i risultati in due file
open(1,FILE=’report.dat’,STATUS=’unknown’)
open(2,FILE=’reportIND.dat’,STATUS=’unknown’)
DO j=1,c
u = 1
DO i=1,2**n
write(1,*) (j-1)*e, R(j,u+1), R(j,u) !funzione d’onda
u = u+2
END DO
END DO
DO j=1,c
u = 1
write(2,*) (j-1)*e, IND(j) !indeterminazione
u = u+2
END DO
stop
end program
97
!--------------------------------------------------------------------------! DISCRETE FOURIER TRANSFORM
!--------------------------------------------------------------------------SUBROUTINE four1(data,nn,isign)
INTEGER isign,nn
REAL data(2*nn)
INTEGER i,istep,j,m,mmax,n
REAL tempi,tempr
DOUBLE PRECISION theta,wi,wpi,wpr,wr,wtemp
n=2*nn
j=1
do 11 i=1,n,2
if(j.gt.i)then
tempr=data(j)
tempi=data(j+1)
data(j)=data(i)
data(j+1)=data(i+1)
data(i)=tempr
data(i+1)=tempi
endif
m=n/2
1
if ((m.ge.2).and.(j.gt.m)) then
j=j-m
m=m/2
goto 1
endif
j=j+m
11
2
12
continue
mmax=2
if (n.gt.mmax) then
istep=2*mmax
theta=6.28318530717959d0/(isign*mmax)
wpr=-2.d0*sin(0.5d0*theta)**2
wpi=sin(theta)
wr=1.d0
wi=0.d0
do 13 m=1,mmax,2
do 12 i=m,n,istep
j=i+mmax
tempr=sngl(wr)*data(j)-sngl(wi)*data(j+1)
tempi=sngl(wr)*data(j+1)+sngl(wi)*data(j)
data(j)=data(i)-tempr
data(j+1)=data(i+1)-tempi
data(i)=data(i)+tempr
data(i+1)=data(i+1)+tempi
continue
wtemp=wr
98
wr=wr*wpr-wi*wpi+wr
wi=wi*wpr+wtemp*wpi+wi
13
continue
mmax=istep
goto 2
endif
return
END
99
Bibliografia
[1] M.A. Nielsen, I. L. Chuang - Quantum Computation and Quantum
Information - Cambridge University Press
[2] M. Le Bellac - Quantum Information and Quantum Computation,
Cambridge University Press
[3] Jurgen Audretsch - Entangled World - Wiley VCH
[4] S. Lloyd - Il programma dell’universo - Giulio Einaudi editore
[5] G. Benenti, G. Strini - Quantum simulation of the single-particle
Schrödinger equation - Am. J. Phys. 76 (7) July 2008
[6] Berman, Doolen, Mainieri, Tsifrinovich - Introduction to Quantum
Computers - World Scientific Publishing
[7] Anton Zeilinger - Il velo di Einstein - Einaudi Editore
[8] Press, Flannery, Teukolsky, Vetterling - Numerical Recipes in Fortran Cambridge University Press
[9] J. J. Sakurai - Modern Quantum Mechanics - Pearson Education
[10] L. Landau - L. Lifshitz- Quantum Mechanics: non-relativistic theory Butterworth-Heinemann
100