Corso di Laurea in Chimica e Tecnologie Farmaceutiche

Corso di Laurea in Chimica e Tecnologie Farmaceutiche
Prova scritta di Fisica
Appello del 27/01/2011 A.A. 2010-11
1) Un treno sale su un tratto inclinato di 8.5° rispetto all’orizzontale con velocità costante in
modulo v = 18.2 m/s rispetto al suolo, mentre piove. La pioggia, rispetto al piano orizzontale,
cade esattamente secondo la verticale con una velocità vp = 10 m/s. Calcolare la velocità, in
modulo, direzione e verso, con cui è vista cadere la pioggia rispetto alla verticale, da un
osservatore fermo sul treno che guarda da un finestrino laterale.
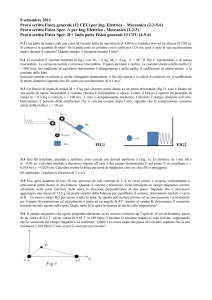
2) Con riferimento al sistema in fig. 1 (con M = 1.5 Kg e m = 0.5 Kg), se il coefficiente di attrito
dinamico fra la superficie orizzontale e il blocco M è D = 0.25, la superficie di contatto fra M e
m è priva di attrito, F = 18.1 N e la massa m non si muove rispetto ad M, calcolare l’
accelerazione del sistema e il valore dell’angolo .
3) Nel dispositivo in fig.2, realizzato con tubi cilindrici, scorre, con moto ideale, aria di densità
aria = 1.29 Kg/m3. L’area della sezione stretta del tubo (punto A) è 1/3 della area della sezione
larga (punto B). Il tubo a forma di U è pieno di acqua (acqua = 1000 Kg/m3) e la differenza di
altezza fra i livelli dell’acqua nei due lati è h = 1,53 cm. Calcolare il rapporto fra le velocità
dell’aria in A e B e il valore della velocità in B.
4) Si vuole fondere, operando a pressione atmosferica, un lingotto di argento di massa m = 5 Kg
inizialmente a una temperatura T = 21 °C. Sapendo che la temperatura di fusione dell’argento è
961 °C, la capacità termica è c = 235 J/(Kg°C) e il calore latente di fusione è  = 88.3 KJ/Kg
calcolare il calore che occorre fornire alla massa m, trascurando l’aumento di volume della
sostanza. Valutare quanto calore in più deve essere fornito se il volume aumenta di 310-6 m3
nella fase di riscaldamento e di 610-6 m3 nella fase di fusione.
5) Una spira circolare di raggio r =5 cm, realizzata con un filo metallico di sezione S=2.1 mm2 e
resistività  = 9.310-8 mΩ, è immersa in un campo magnetico uniforme ma variabile nel tempo
B(t) = B0t con B0 = 0.6 T/s. La normale alla spira forma un angolo  con la direzione di B e si
osserva che nella spira circola una corrente di 0.12 A. Calcolare il valore di  e il momento
meccanico necessario a tenere ferma la spira all’istante di tempo t = 3.
B
F
A
m
M
fig. 1
 h
fig. 2