Campo magnetico nei punti dell’asse di una spira circolare percorsa da corrente elettrica
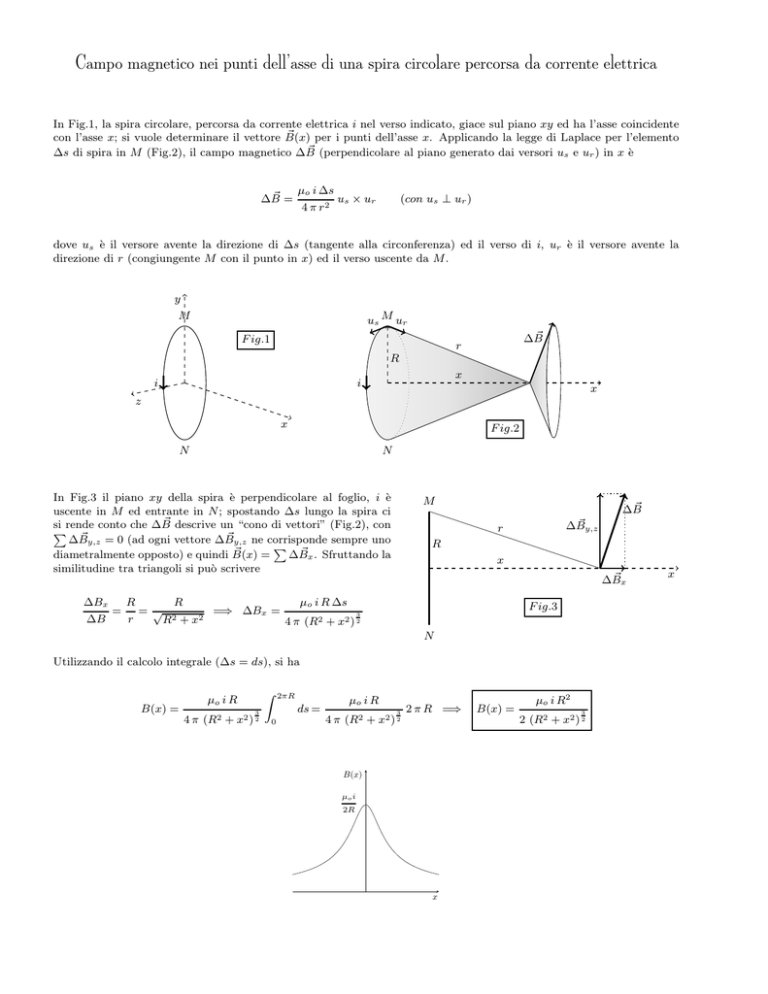
In Fig.1, la spira circolare, percorsa da corrente elettrica i nel verso indicato, giace sul piano xy ed ha l’asse coincidente
~
con l’asse x; si vuole determinare il vettore B(x)
per i punti dell’asse x. Applicando la legge di Laplace per l’elemento
~ (perpendicolare al piano generato dai versori us e ur ) in x è
∆s di spira in M (Fig.2), il campo magnetico ∆B
~ =
∆B
µo i ∆s
4 π r2
(con us ⊥ ur )
us × ur
dove us è il versore avente la direzione di ∆s (tangente alla circonferenza) ed il verso di i, ur è il versore avente la
direzione di r (congiungente M con il punto in x) ed il verso uscente da M .
y
M
us M ur
F ig.1
~
∆B
r
R
i
x
i
x
z
x
F ig.2
N
N
In Fig.3 il piano xy della spira è perpendicolare al foglio, i è
uscente in M ed entrante in N ; spostando ∆s lungo la spira ci
~ descrive un “cono di vettori” (Fig.2), con
si rende conto che ∆B
P ~
~ y,z ne corrisponde sempre uno
∆By,z = 0 (ad ogni vettore ∆B
P ~
~
diametralmente opposto) e quindi B(x)
=
∆Bx . Sfruttando la
similitudine tra triangoli si può scrivere
∆Bx
∆B
=
M
~
∆B
~ y,z
∆B
r
R
x
~x
∆B
R
µo i R ∆s
= √
=⇒ ∆Bx =
3
2
2
r
R +x
4 π (R2 + x2 ) 2
R
F ig.3
N
Utilizzando il calcolo integrale (∆s = ds), si ha
B(x) =
µo i R
4 π (R2 + x2 )
3
2
Z
0
2πR
ds =
µo i R
4 π (R2 + x2 )
3
2
2 π R =⇒
B(x)
µo i
2R
x
B(x) =
µo i R2
3
2 (R2 + x2 ) 2
x












