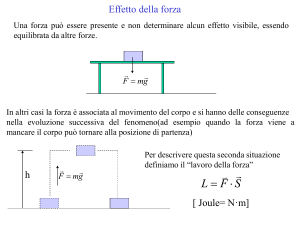
La definizione di lavoro è un prerequisito.
Teorema delle forze vive
Partiamo dalla definizione di lavoro compiuto da una forza F~ (s) su un
segmento di traiettoria infinitesimo d~s:
dL = F~ (s) · d~s = Ft ds
(1)
con Ft si è indicata la forza parallela allo spostamento.
Ma dalla seconda legge di Newton, F~ = m~a, ovvero Fp = mat , quindi
dL = mat ds
(2)
Notiamo che la componente tangenziale at della accelerazione ~a fa variare
il modulo della velocità v mentre la componente radiale ar fa variare solotanto
la direzione orientata v̂. Tenendo presente questo fatto possiamo scrivere:
at =
dv
dt
(3)
quindi:
dv
ds
(4)
dt
La velocità è funzione del tempo, ma è anche funzione della traiettoria s
poiché il modulo della velocità del corpo varia in modo spocifico mentre esso
si muove lungo la traiettoria sotto l’azione della forza F~ (s). Allora:
dL = m
dv
dv ds
dv ds
dv
=
=
=v
dt
dt ds
ds dt
ds
Sostituendo nell’espressione del lavoro:
(5)
dv
ds = mvdv
(6)
ds
A questo punto possimao calcolare il lavoro compiuto sul corpo mentre
percorre la traiettoria finita tra si e sf :
dL = mv
Z sf
Z vf
1
1
1
(7)
mvdv = mv 2 |vvfi = mvf2 − mvi2
2
2
2
si
vi
Data l’importanza e la generalità di questo risultato (ricordiamo che non
abbiamo posto alcuna limitazione alla forza F~ ), chiamiamo la grandezza
1
mv 2 energia cinetica K (l’energia cinetica è l’energia associata al moto del
2
corpo) e l’ultima relazione diviene:
L=
dL =
2
L = Kf − Ki = ∆K
(8)
La variazione di energia cinetica di un corpo è uguale al lavoro totale
compiuto su di esso (lavoro compiuto dalla forza risultante sul corpo).
Forze conservative e conservazione dell’energia
Le forze conservative hanno un modo speviale di compiere lavoro, quindi,
le forze conservative vengono definite in base al loro modo di compiere lavoro.
Definizione di forza conservativa
Una forza è conservativa se il lavoro compiuto da questa forza su un corpo
lungo un cammino chiuso (in cui il punto iniziale e finale coincidono) è nullo,
ovvero se il lavoro non dipende dalla particolare traiettoria, ma solo dal punto
iniziale e finale.
I
L=
F~c · d~s = 0
(9)
ovvero
L=
Z sf
si
F~c · d~s = f (sf ) − f (si )
(10)
dove con f si è indicata la funzione integrata nei punti iniziale e finale.
~ = µd mg tra un corpo
Esempio. Verificare che la forza di attrito |Fa|
puntiforme di massa m (in movimento) e la superficie orizzontale, non è una
forza conservativa (calcolare il lavoro lungo una traiettoria chiusa).
Questa proprietà è importante e generale, nell’ambito di tutte le forze che
la verificano. Allora, definiamo una funzione energia potenziale (funzione solo
dei punti iniziale e finale e non della traiettoria particolare tra di essi), che
rappresenti il lavoro di una forza conservativa:
L = −(U (sf ) − U (si )) = −∆U
(11)
(la necessità del segno meno sarà chiara in seguito e non deve comunque
preoccuparci: stiamo introducendo noi questa funzione e la possiamo definire
sia con lo stesso segno del lavoro o con segno opposto, purché poi manteniamo
la coerenza con la nostra definizione).
3
Esempi. Calcolare l’energia potenziale per la forza peso e per la forza
elastica.
Conseguenza di questa definizione: la conservazione dell’energia
Il teorema dell’energia cinetica ci dice che L = ∆K e vale PER OGNI
FORZA, quindi anche per forze conservative. Me se la forza è conservativa,
si ha anche che L = ∆U (ricordate, solo per forze conservative, altrimenti U
non esiste). Allora, se la forza che agisce su un corpo è conservativa possiamo
scrivere
∆K = −∆U
(12)
da cui, ricordando, con un po’ di passaggi algebrici si ricava:
Kf − Ki − (Uf − Ui ) ⇒ Kf + Uf = Ki + Ui )
(13)
Questo risultato, importantissimo, dice che la somma della energia cinetica e dell’energia potenziale di un corpo in un punto (arbitrario) della sua
traiettoria è uguale alla somma della sua energia cinetica e della sua energia
potenziale in un altro punto (arbitrario) della sua traiettoria. Ovvero, la
somma dell’energia cinetica e dell’energia potenziale di un corpo è costante
lungo il moto del corpo.
L’unica limitazione di questo risultato è nel fatto che la forza agente sul
corpo è conservativa. Quindi, lo riassumiamo definendo un’altra grandezza,
detta energia meccanica E del corpo, come la somma dell’energia cinetica e
l’energia potenziale e scrivendo, in maniera del tutto equivalente:
Ei = Ef
(14)
E = costante
(15)
∆E = 0
(16)
oppure
oppure