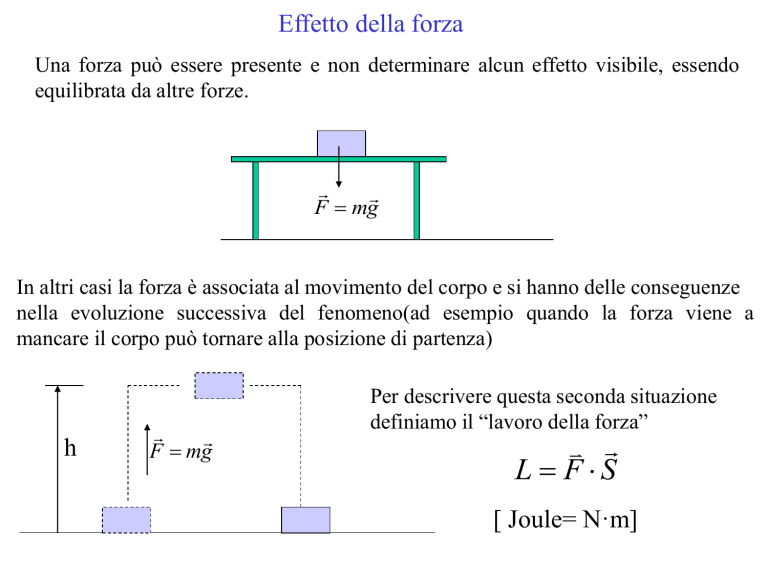
Effetto della forza
Una forza può essere presente e non determinare alcun effetto visibile, essendo
equilibrata da altre forze.
F mg
In altri casi la forza è associata al movimento del corpo e si hanno delle conseguenze
nella evoluzione successiva del fenomeno(ad esempio quando la forza viene a
mancare il corpo può tornare alla posizione di partenza)
h
F mg
Per descrivere questa seconda situazione
definiamo il “lavoro della forza”
L F S
[ Joule= N·m]
LAVORO DI UNA FORZA
Se su un corpo agisce una forza F costante, il lavoro
compiuto dalla forza per uno spostamento s è:
L Fs cos F s
F
s
Il lavoro è una quantità scalare
2
LAVORO DI UNA FORZA
Una persona che trascina una cassa
lungo il pavimento. Il lavoro compiuto
dalla forza F è L=F·d·cos, dove d è lo
spostamento.
Il lavoro compiuto sul
pacchetto in questo
caso è nullo poiché F
è perpendicolare allo
spostamento d.
3
LAVORO DI UNA FORZA
Il lavoro può essere:
positivo
nullo
negativo
4
UNITÀ DI MISURA DEL LAVORO
L’unità di misura del lavoro nel S.I. si chiama joule
(J), ed è pari al lavoro compiuto dalla forza di 1 N il
cui punto di applicazione si sposta di 1 m
parallelamente e nello stesso verso della forza.
J N m kg m s
2
2
5
Piano inclinato
L
h Lsen
mg
mgsen
Lavoro F S Fa L mg sen L
Lavoro mg L sen mg h
Lavoro per forze non costanti e traiettorie curvilinee
Nel caso di traiettorie non rettilinee e di forze non costanti, il lavoro fatto dalle forze
dal punto A al punto B è la somma dei contributi di spostamenti elementari rettilinei
e forze locali lungo la traiettoria
LAB
Fi Si
LAB
F dS
ì
B
A
B
LAB ( Fx dx Fy dy Fz dz)
A
A
dS
B
Lavoro ed Energia Cinetica (teorema delle forze vive)
B
A
L F ds
B
A
B
B
ds
dv
L m
ds mdv
mv dv
dt
dt A
A
A
B
B
B
B
B
A
A
A
A
L m(v x dv x v y dv y v z dv z ) mvx dv x mvy dv y mvz dv z
2 B
v
Lm x
2
m
A
vy
2 B
2
A
1
1
2
2
mvB mvA
2
2
L WB WA
L
2 B
v
m z
2
A
1
2
2
2
m vx v y vz
2
B
A
Applicazioni Teorema delle forze vive (1)
• Un corpo di massa m cade da un’altezza di 10 m ; con quale velocità tocca terra?
a
m
mg
La b
h=10 m
La b
F S F S cos m g h
1
2
Wb Wa mvb 0
2
1
2
mvb m g h
2
vb 2 g h 2 9,8 10 14m / s
b
Applicazioni Teorema delle forze vive (2)
• Un tubo radiogeno viene alimentato a 100 kV. Con quale velocità gli elettroni
colpiscono l’anodo?
V
dV
qe
D
dV
LK A F S F S
qe D kV qe
D
1
1
1
2
2
2
LK A me v A me vK me v A
2
2
2
F
1
2
me v A
2
q
v A 2 dV e
me
dV qe
D
Forze Conservative
Un campo di forze si dice conservativo quando il lavoro fatto dalle forze del
campo per spostare un punto materiale da una posizione A ad una posizione B
è indipendente dalla traiettoria seguita.
Si può anche dire che il lavoro compiuto dalle forze del campo conservativo
in una traiettoria chiusa e nullo.
B
1
2
3
A
F ds F ds F ds
1
2
3
Energia Potenziale
Nel caso di forze conservative il lavoro delle forze del campo tra due punti A e B
non dipende dalla traiettoria ma solo dalle posizioni dei due punti; il lavoro sarà
quindi determinato unicamente dalle coordinate spaziali dei due punti.
LAB f ( x A , y A , z A , xB , yB , z B )
In termini matematici, esisterà una funzione U ( x, y, z )
tale che:
LAB U ( x A , y A , z A ) U ( xB , y B , z B )
La funzione scalare
U ( x, y, z ) viene chiamata Energia Potenziale
Per ogni campo di forze conservative abbiamo una particolare forma di energia
potenziale associata (es. energia potenziale gravitazionale, elettrostatica, elastica).
Energia Potenziale
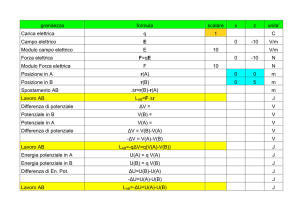
Energia Potenziale dei Campi conservativi più frequenti:
U P mgh
Forza peso
1 Qq
UE
40 r
Forza elettrostatica
1
2
U M k ( x x0 )
2
Molla
ENERGIA POTENZIALE
L mg h
mg ( z1 z 2 )
mgz1 mgz2
U1 U 2
U = mgz
P
s
h
z1
z2
Energia potenziale gravitazionale
L’energia potenziale rappresenta la potenzialità che un
corpo possiede a compiere lavoro in virtù della sua
posizione.
14
Principio di conservazione dell’energia meccanica totale
F ds WB WA
B
Per qualsiasi tipo di forza vale la relazione
LAB
A
F
Per forze conservative vale la relazione
LAB
F ds U A U B
A
Per le sole forze conservative valgono entrambe
WB WA U A U B
B
ed in qualunque punto della traiettoria si ha che:
A
W U costante
Se questo non avviene si ha l’evidenza di forze non conservative.
CONSERVAZIONE DELL’ENERGIA
L’energia si trasforma, non si crea né si distrugge
16
La potenza
La potenza:
L
P
t
joule watt
sec
La potenza esprime la capacità di compiere lavoro nel tempo
L F s
P
F v
t
t
Nota Bene: il kilowattora è una energia, non una potenza.
La corrente elettrica si paga in kilowattora
Riassumendo…..
Le forze sono le cause del moto …….. Conosciamo quattro tipi di forze……….
L’effetto della forza è descritto da tre leggi fondamentali ( principi)…………
Quando una forza sposta il suo punto d’azione ( spostamento) si può avere lavoro…..
Il lavoro si calcola come prodotto scalare ……………….
Il lavoro compiuto da una forza tra un punto a ed un punto b è sempre
corrispondente alla ………………
Esistono forze particolari per le quali il lavoro tra due punti non dipende dalla
traiettoria ma solo dalle coordinate dei due punti …………
Per le forze “ Conservative “ si conserva l’energia meccanica totale…………