Corso di Elettronica Digitale Anno Accademico 2006/2007 Dato il

Università degli Studi di Cagliari
Dipartimento di Ingegneria Elettrica ed Elettronica
Laboratorio di Elettronica
Corso di Elettronica Digitale
Anno Accademico 2006/2007
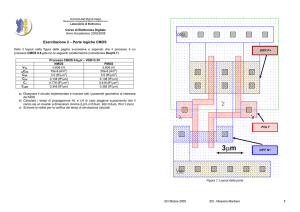
Dato il layout nella figura della pagina successiva e sapendo che il processo è un
processo CMOS 90 nm con le seguenti caratteristiche (considerare Keq=0.7):
VTH
VDSAT
µCOX
λ
COX
COV
CJ
CJSW
Processo CMOS 90nm – VDD=1V
NMOS
0.371 (V)
0.175 (V)
300e-6 (A/V2)
0.71 (1/V)
15.35 (fF/µm2)
0.05 (fF/µm)
1.07 (fF/µm2)
0.126 (fF/µm)
DIFF P+
PMOS
0.371 (V)
0.175 (V)
147e-6 (A/V2)
0.9 (1/V)
15.35 (fF/µm2)
0.05 (fF/µm)
1.26 (fF/µm2)
0.129 (fF/µm)
a) Disegnare il circuito implementato e ricavare tutti i parametri geometrici di interesse
dei MOS (VDD è l’alimentazione e VSS la massa)
b) Calcolare i tempi di propagazione HL e LH di caso peggiore supponendo che il
carico sia un inverter a dimensioni minime (Lp=Ln=90nm, Wp=360nm, Wn=180nm)
c) Scrivere la netlist per la verifica dei tempi di simulazione calcolati
POLY
450nm
DIFF N+
Figura 1: Layout della porta
23 Ottobre 2006
ED - Massimo Barbaro
1
2
a1) Funzionalità
Per individuare la funzione implementata si può partire dalla PDN o dalla PUN. Ovviamente
la PDN sarà costituita da tutti gli NMOS (quelli in basso) e la PUN dai PMOS (quelli in alto,
dentro la NWELL).
Per trovare gli NMOS cerchiamo tutte le intersezioni fra POLY (polisilicio) e DIFF N+
(diffusione n+). Ce ne sono solo 2 che danno luogo a 2 transistor in serie fra uscita e massa.
Nella PUN invece ci sono (cerco le intersezioni fra POLY e DIFF P+) 2 PMOS ma sono in
parallelo fra l’uscita e la VDD.
b) Tempi di propagazione
I transistor sono già dimensionati quindi possiamo identificare immediatamente il caso
peggiore nel caso della commutazione HL: il caso in cui il transistor M4 (quello più in basso)
commuta per ultimo (quando M3 già conduce) essendo così costretto a pilotare tutte le
capacità parassite intermedie. Nel caso della commutazione LH il caso peggiore è sempre
quello in cui conduce uno solo dei 2 rami.
Transizione HL
La commutazione peggiore è quella in cui il segnale A commuta e B=1. In tal caso si richiede
di pilotare sia il nodo di uscita Z che il nodo parassita N1.
Calcolo di CL
Per calcolare il tempo di propagazione col metodo di Elmore bisogna innanzitutto calcolare le
varie capacità parassite. Bisogna andare a vedere uno per uno tutti i nodi del circuito che
devono essere scaricati (siamo in una commutazione HL) e tenere conto della capacità
parassite che vi sono connesse. Poiché alcuni segnali sono già a 1 ed altri a 0 ci possono
essere dei nodi interni (nel nostro caso c’è un solo nodo interno, il nodo N1) che sono sul
percorso di scarica e sono connessi inizialmente all’uscita e devono perciò essere scaricati
insieme ad essa.
Figura 2: Schematico della porta
a2) Dimensioni
Le dimensioni dei vari MOS sono indicate in tabella, ma i drain dei 2 pmos sono
COINCIDENTI (quindi possiamo considerare che metà dell’area e del perimetro della
diffusione appartengano al drain di M1 e metà a quello di M2). Analogamente source di M3 e
drain di M4 sono COINCIDENTI (sono la stessa diffusione) quindi metà del perimetro
dell’area saranno attribuiti al source di M3 e metà al drain di M4.
PMOS
2
2
NOME
W (um)
L (um)
AD (um )
PD (um)
AS (um )
PS (um)
M1
0.540
0.090
0.0972
0.360
0.1944
1.17
M2
0.540
0.090
0.0972
0.360
0.1944
1.17
NMOS
2
2
NOME
W (um)
L (um)
AD (um )
PD (um)
AS (um )
PS (um)
M3
0.180
0.090
0.081
0.990
0.0162
0.180
M4
0.180
0.090
0.0162
0.180
0.081
0.990
Nodo Z (vedi Figura 4 in fondo al documento):
Essendo il nodo Z l’uscita, deve sicuramente essere scaricato in una transizione HL. Vi sono
collegate le seguenti capacità parassite:
Capacità di diffusione:
Cdb1 = Keq ( CJ AD1 + CJSW PD1 ) = 0.118 fF
Cdb2 = Keq ( CJ AD2 + CJSW PD2 ) = 0.118 fF
Cdb3 = Keq ( CJ AD3 + CJSW PD3 ) = 0.148 fF
Capacità di gate:
Cgd1 = COV W1 = 0.027 fF
(andrà poi pesata 2 per tenere conto dell’effetto Miller
perché connessa fra ingresso ed uscita)
Cgd2 = COV W2 = 0.027 fF
(non va moltiplicata per 2 perché non è connessa fra
ingresso ed uscita ma fra uscita ed una tensione costante)
Cgd3 = COV W3 = 0.009 fF (non è pesata 2 per effetto Miller perché non è connessa fra
ingresso ed uscita ma solo fra uscita ed una tensione costante)
Il carico offerto dall’inverter è:
CL’ = Cgp + Cgn = COX ( Wp Lp + Wn Ln ) = COX ( Wp + Wn ) Lmin = 0.746 fF
Cpz = ( Cdb1 + Cdb2 + Cdb3 + 2Cgd1 + Cgd2 + Cgd3 ) = 1.22 fF
Nodo N1 (vedi Figura 5 in fondo al documento):
Il nodo N1 deve essere scaricato perché è inizialmente connesso all’uscita (tramite M3 che è
chiuso essendo B=1). Vi sono collegate le seguenti capacità parassite:
Capacità di diffusione:
Csb3 = Keq ( CJ AS3 + CJSW PS3 ) = 0.028 fF
Cdb4 = Keq ( CJ AD4 + CJSW PD4 ) = 0.028 fF
Capacità di gate:
Cgs3 = COV W3 = 0.009 fF
(non è pesata 2 per effetto Miller perché non è connessa fra
ingresso ed uscita ma solo fra uscita ed una tensione costante)
Cgd4 = COV W4 = 0.009 fF
(andrà poi pesata 2 per tenere conto dell’effetto Miller
perché connessa fra ingresso ed uscita)
Cpn1 = ( Csb3 + Cdb4 + Cgs3 + 2Cgd4 ) = 0.083 fF
23 Ottobre 2006
ED - Massimo Barbaro
1
3
23 Ottobre 2006
ED - Massimo Barbaro
1
4
c) Netlist spice
Calcolo di Reqn
Bisogna a questo punto trovare la corrente di saturazione di ciascun transistor per potere
calcolare la sua RON. Si tenga presente che gli NMOS hanno lo stesso dimensionamento
quindi le loro RON sono identiche.
Isatn3 = Isatn4 = µn COX (W/L)3 VDSATn (VDD-VTH-VDSATn/2) = 57 uA
Reqn3 = Reqn4 = ¾ VDD / ISATn = 13.2kΩ
Applicando il metodo di Elmore:
tpHL = 0.69 [ Reqn4 Cpn1 + ( Reqn3 + Reqn4) Cpz ]
= 0.69 Req (Cpn1 + 2Cpz) = 23 psec
Transizione LH
Calcolo di CL
La Cpz è evidentemente identica alla transizione HL (comunque si fanno gli stessi
ragionamenti) e non ci sono nodi intermedi da pilotare:
* Simulazione Nand
* Inclusione modelli
.include models.dat
* Circuito (la sintassi spice è case-insensitive)
* Nand
M1 out1 inA vdd vdd P90 w=540n l=90n ad=.097e-12 as=.194e-12 pd=.36u ps=1.17u
M2 out1 inB vdd vdd P90 w=540n l=90n ad=.097e-12 as=.194e-12 pd=.36u ps=1.17u
M3 out1 inB 1 0 N90 w=180n l=90n ad=.081e-12 as=.0162e-12 pd=.99u ps=.18u
M4 1 inA 0 0 N90 w=180n l=90n ad=.0162e-12 as=.081e-12 pd=.18u ps=.99u
* Carico
M5 out2 out1 vdd vdd P90 w=360n l=90n
M6 out2 out1 0 0 N90 w=180n l=90n
* Alimentazione (il nodo 0 è sempre la massa)
Vdd vdd 0 dc 1
* Generatore di Ingresso
VinB inB 0 1
Vin inA 0 dc 0 pulse 0 1 200p 0.1p 0.1p 200p 400p
*Analisi in transitorio
.tran 1p 800p
.end
Calcolo di Reqn
Isatp1 = µp COX (W/L)1 VDSATp (VDD-VTH-VDSATp/2) = 84 uA
Reqp1 = ¾ VDD / ISATp = 9kΩ
tpLH = 0.69 Req Cpz = 7.6 psec
Figura 3: Simulazione in transitorio
L’errore rispetto ai valori calcolati (grande soprattutto per LH) è dovuto alle approssimazioni
utilizzate nelle formule ed anche al fenomeno, non calcolato da noi, del forte
accoppiamento fra la rapida variazione dell’ingresso e l’uscita, che genera gli spike (i picchi)
molto pronunciati nella transizione. Come si vede la nostra approssimazione di modello del
primo ordine non è accurata perché in tale caso non si avrebbe overshoot nell’uscita che
comincerebbe subito a decrescere esponenzialmente. In realtà l’uscita prima cresce fino
addirittura a superare VDD e solo dopo comincia a decrescere esponenzialmente. Inoltre
non abbiamo considerato che per alcuni MOS la capacità Cgd o Cgs non è data solo dal
contributo di overlap ma anche dal contributo del canale (quello che dipende dalla regione
di funzionamento).
23 Ottobre 2006
ED - Massimo Barbaro
1
5
23 Ottobre 2006
ED - Massimo Barbaro
1
6
Figura 4: Capacità parassite connesse al nodo Z - HL
Figura 5: Capacità parassite connesse al nodo N1 - HL
23 Ottobre 2006
ED - Massimo Barbaro
1
7