Riassunto
In questa esercitazione e' stato introdotto l'ambiente MatLab ed e' stato mostrato l'ambiente in funzione
riepilogando i comandi di base come l'assegnamento di scalari, array e matrici a variabili, operazioni
tra matrici, ecc. Per maggiori riferimenti su questi comandi consultare la dispensa del corso.
Successivamente sono stati svolti gli esercizi che trovate in fondo alla pagina.
Slide presentate.
Gli esercizi svolti sono i seguenti:
1.
2.
3.
4.
5.
6.
Un esempio di cinematica
Equazioni di secondo grado
Sistemi di equazioni lineari
Confronti
Vettori logici
Cosa Stampa?
Esercizio1.Un esempio di cinematica
Due treni partono da due stazioni adiacenti, che distano 15km, viaggiando a velocità di 50m/s e 30m/s
in direzione opposta
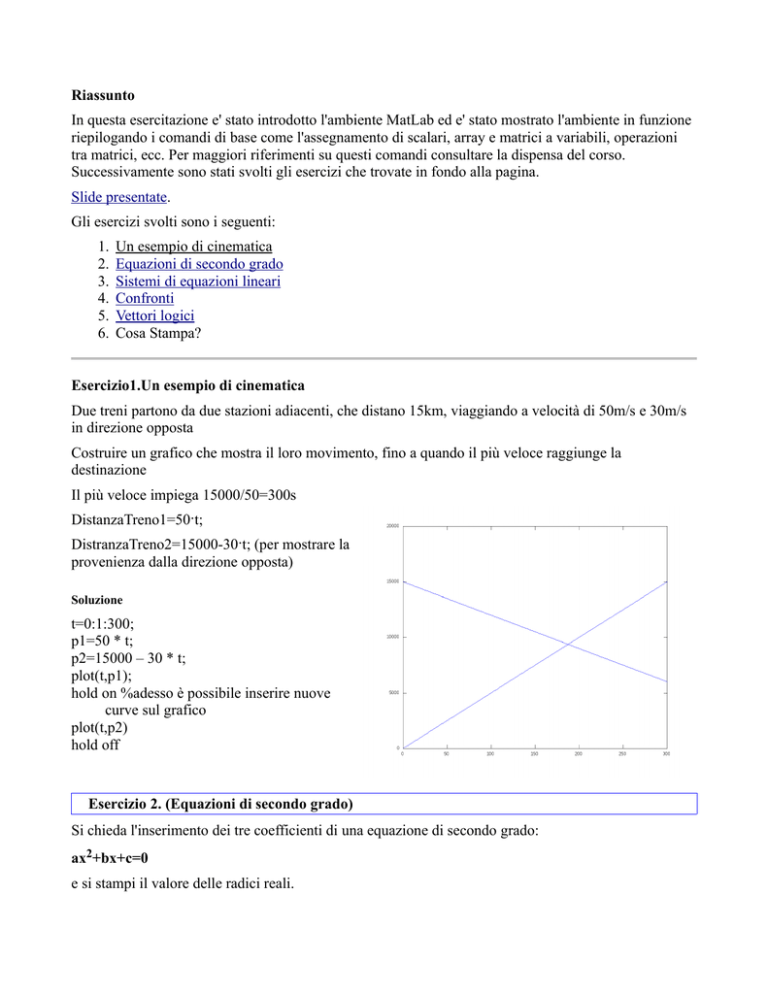
Costruire un grafico che mostra il loro movimento, fino a quando il più veloce raggiunge la
destinazione
Il più veloce impiega 15000/50=300s
DistanzaTreno1=50·t;
DistranzaTreno2=15000-30·t; (per mostrare la
provenienza dalla direzione opposta)
Soluzione
t=0:1:300;
p1=50 * t;
p2=15000 – 30 * t;
plot(t,p1);
hold on %adesso è possibile inserire nuove
curve sul grafico
plot(t,p2)
hold off
Esercizio 2. (Equazioni di secondo grado)
Si chieda l'inserimento dei tre coefficienti di una equazione di secondo grado:
ax2+bx+c=0
e si stampi il valore delle radici reali.
Soluzione
Bisogna calcolare il discriminante dell'equazione con la formula: b2-4ac
Se e' positivo abbiamo due radici distinte, se e' nullo le radici sono reali e coincidenti, se e' negativo le
radici non sono reali.
Codice
a=input('Inserire a: ');
b=input('Inserire b: ');
c=input('Inserire c: ');
delta=b^2-4*a*c;
if delta < 0
disp('L''equazione non ha soluzioni reali');
elseif delta==0
disp(['x=' num2str(-b/(2*a))]);
else
disp(['x1=' num2str((-b-sqrt(delta))/(2*a)) ' x2=' ...
num2str((-b+sqrt(delta))/(2*a))]);
end
Esecuzione
Inserire a:
Inserire b:
Inserire c:
L'equazione
1
1
1
non ha soluzioni reali
Inserire a: 1
Inserire b: 2
Inserire c: 1
x=-1
Inserire a: 1
Inserire b: 1
Inserire c: -1
x1=-1.618 x2=0.61803
Esercizio 3. (Sistemi di equazioni lineari)
Si scriva uno script che chieda l'inserimento dei coefficienti e dei termini noti di un sistema di
equazioni di primo grado in M equazioni e N incognite. Dopodiche' si calcoli la soluzione del sistema.
Si consideri solo il caso in cui M e' uguale a N.
Soluzione
Il sistema puo' essere rappresentato in forma di matrice:
Dall'algebra lineare sappiamo che i valori delle incognite che corrispondono alla soluzione del sistema
sono contenuti nella matrice data dalla moltiplicazione dell'inverso della matrice dei coefficienti A per
il vettore dei termini noti.
La soluzione e' quindi S=A-1b che in Matlab equivale all'operazione di divisione sinistra: S=A\b
Codice
N=input('Inserire il numero di equazioni e di incognite: ');
x = 1;
while x <= N % righe (equazioni)
y = 1;
while y <= N % colonne (incognite)
A(x,y)=input(['inserire coefficiente incognita ' num2str(y)
.
' dell''equazione ' num2str(x) ': ']);
y = y + 1;
end
b(x)=input(['inserire termine noto equazione ' num2str(x) ': ']);
x = x+1;
end
A
b
S=A\b'
Esecuzione
inserire
inserire
inserire
inserire
inserire
inserire
inserire
numero di equazioni e di incognite: 2
coefficiente incognita 1 dell'equazione
coefficiente incognita 2 dell'equazione
termine noto equazione 1: 4
coefficiente incognita 1 dell'equazione
coefficiente incognita 2 dell'equazione
termine noto equazione 2: -1
A =
1
-6
2
5
4
-1
b =
S =
1.2941
1.3529
1: 1
1: 2
2: -6
2: 5
Esercizio 4. (Confronti)
Si scriva uno script che chiede di inserire una sequenza di N numeri, dopodiche' si inserisca un
ulteriore numero e si dica se tutti i numeri della sequenza sono minori, uguali o maggiori di tale
numero.
Soluzione
Sono presenti due modi per risolvere questo problema. Il secondo evita l'utilizzo del ciclo ed e' piu'
efficiente e leggibile.
Codice
N=input('inserire N: ');
x = 1;
while x <= N
a(x) = input('inserire numero: ');
x = x +1;
end
x = 1;
M=input('inserire M: ');
minori=true;
maggiori=true;
uguali=true;
while x <= N
if a(x)>M
minori=false;
uguali=false;
elseif a(x)<M
maggiori=false;
uguali=false;
else
maggiori=false;
minori=false;
end
x = x +1;
end
if minori
disp('I numeri della sequenza sono minori del numero dato');
else
disp('I numeri della sequenza non sono minori del numero dato');
end
if maggiori
disp('I numeri della sequenza sono maggiori del numero dato');
else
disp('I numeri della sequenza non sono maggiori del numero dato');
end
if uguali
disp('I numeri della sequenza sono uguali al numero dato');
else
disp('I numeri della sequenza non sono uguali al numero dato');
end
Codice alternativo (piu' efficiente) per il ciclo
if sum(a<M) < N
minori = false;
end
if sum(a>M) < N
maggiori = false;
end
if sum(a==M) < N
uguali = false;
end
Esecuzione
inserire
inserire
inserire
inserire
inserire
inserire
inserire
I numeri
I numeri
I numeri
N: 5
numero: 1
numero: 2
numero: 3
numero: 4
numero: 5
M: 6
della sequenza sono minori del numero dato
della sequenza non sono maggiori del numero dato
della sequenza non sono uguali al numero dato
Esercizio 5. (Vettori logici)
Si scriva uno script che chieda l'inserimento di una sequenza di N numeri.
1.
2.
3.
4.
Si stampino i valori dei numeri in posizione pari;
Si stampino i valori dei numeri in posizione dispari;
Si stampino i valori dei numeri pari;
Si stampino i valori dei numeri dispari.
Soluzione
Codice
N=input('inserire N: ');
clear a;
x = 1
while x <= N
a(x) = input('inserire numero: ');
end
% stampo soluzione punto 1
a(2:2:N) % stampo soluzione punto 2
a(1:2:N)
% stampo soluzione punto 3
a(mod(a,2)==0)
% stampo soluzione punto 4
a(mod(a,2)==1)
Esecuzione
inserire
inserire
inserire
inserire
inserire
inserire
N: 5
numero:
numero:
numero:
numero:
numero:
ans =
1
4
ans =
3
8
ans =
8
4
ans =
3
1
3
1
8
4
9
9
9
Esercizio 6. (Matrici logiche misteriose)
Date le seguenti matrici a e b si dica cosa stampano le seguenti istruzioni.
a=
1
4
7
2
5
8
3
6
9
b=
9
6
3
8
5
2
7
4
1
1.
2.
3.
4.
5.
6.
a(3,1)
a(8)
a(a==b)
b(a>b|b>a)
a(b)
c=a;c(a>b)=b(a?b).^2
Soluzione 1
>> a(3,1)
ans =
7
L'istruzione accede al valore memorizzato nella riga 3 e colonna 1 della matrice a.
Soluzione 2
>> a(8)
ans =
6
L'istruzione accede al valore memorizzato nell'ottavo elemento della matrice. Gli elementi vengono
contati per colonna. La prima colonna ha i primi 3 elementi, la seconda colonna ha gli altri 3 e cosi' via
fino al nono elemento. In questo caso l'ottavo elemento coincide con l'elemento della seconda riga e
della terza colonna.
Soluzione 3
>> a==b
ans =
0
0
0
0
1
0
0
0
0
In questo caso il vettore logico a==b e' vero (1) soltanto per l'elemento di riga 2 e colonna 2 della
matrice (infatti e' l'unico elemento di a che e' uguale al corrispondente elemento di b).
Soluzione 4
>> a>b
ans =
0
0
0
0
0
1
1
1
1
Questo esercizio e' simile al precedente. Viene prodotta la matrice logica per cui "a>b", cioe' che il
numero di a sia maggiore di b .
Soluzione 4
>> c= b.^2 %(elevamento al quadrato di ogni elemento di b)
c =
81
36
9
64
25
4
49
16
1
>> c= b^2 %(prodotto righe per colonne di b * b)
c =
150
96
42
126
81
36
102
66
30
Soluzione 5
>> c= b.^a %(ogni elemento di b viene elevato al corrispondente elemento di a)
c =
9
1296
2187
64
3125
256
343
4096
1
Nota: non ha senso b^a! Produce: error: can't do A ^ B for A and B both matrices












