CORSO DI LAUREA IN INGEGNERIA ELETTRICA
!
Informatica B
anno accademico 2012-2013
Prof. Danilo ARDAGNA
!
Esercitazione – 16.05.2013
!
!
!
Esercizio 1: Cinematica
!
Due treni partono da due stazioni adiacenti, che distano 15km, viaggiando a velocità di 50m/s e 30m/s in
direzione opposta.
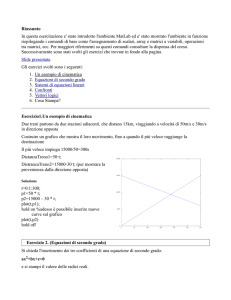
Costruire un grafico che mostri la loro posizione, fino a quando il più veloce raggiunge la destinazione.
!
Il più veloce impiega 15000/50=300s
La distanza percorsa dal treno 1: DistanzaTreno1 = 50·t;
La distanza percorsa dal treno 2: DistanzaTreno2 = 15000 - 30·t;
direzione opposta)
(per mostrare la provenienza dalla
!
!
!
!
!
!
!
!
!
!
!
!!
!!
Esercizio 2: Matrice Triangolare
!
!
!
!
• Creazione dello script treni.m
• Esegui treni nella console
Soluzione
max_t = 15000/50; t=0:1:max_t; distanza_treno_1 = 50*t; distanza_treno_2 = 15000-­‐30*t; plot(t,distanza_treno_1); hold on plot(t,distanza_treno_2); hold off (Estratto dal tema d’esame della prova in itinere B1 2012)
Si scriva uno script in Matlab/Octave che svolge le seguenti operazioni:
1. Definisce una matrice quadrata di interi di dimensione N*N, con N pari a 5.
2. Acquisisce da tastiera una sequenza di valori interi che memorizza nella porzione triangolare superiore
della matrice. La parte triangolare superior della matrice è costituita dalle celle poste sulla diagonal
principale e al di sopra di tale diagonale.
!
!
3. Copia in un array di dimensioni opportune tutti I valori della porzione triangolare di matrice che sono
maggiori di -10.
4. Stampa il contenuto dell’array.
!2
!
!
Soluzione
N=5; for x=1:N for y=x:N M(x,y)=input(sprintf('M(%d,%d)= ',x,y)); end end !
%visualizza M M l=1; for x=1:N for y=x:N if(M(x,y)>-­‐10) a(l)=M(x,y); l=l+1; end end end !
%visualizza a %così a %oppure utilizzando disp disp(a) !
!
Esercizio 3: Rotazione di Matrice
!
Programma che data una matrice a NxN crea una nuova matrice b ruotata di 90 gradi in senso antiorario
rispetto ad a.
Si consideri N=4 e la matrice a inizializzata con i valori
!
!
!
!
[1 2 3
4; 2 3 4 5; 6 7 8 9; 0 0 0 0]
Soluzione
N=4; a = [1 2 3 4; 2 3 4 5; 6 7 8 9; 0 0 0 0]; for x=1:N for y=1:N b(N+1-­‐y,x)=a(x,y); end end !
%stampo la matrice originale a %stampo la matrice ruotata b !
!
!
!
Soluzione 2 N=4; a=[1 2 3 4; 2 3 4 5; 6 7 8 9; 0 0 0 0]; !2
!3
%utilizzo la funzione di MATLAB rot90 a !
!
Esercizio 4: Sequenza palindroma !
!
!
!
!
!
!
b=rot90(a) Si scriva uno script che chiede l’inserimento di una sequenza di N numeri e alla fine dice se la sequenza è
palindroma o no.
Si ricorda che una sequenza è palindroma se risulta uguale letta da sinistra verso destra o da destra verso
sinistra.
Soluzione
a=input('Inserire parola: '); N = length(a); palindroma = true; for x=1:N/2 if a(x)~= a(N-­‐x+1) palindroma=false; end end !
if palindroma disp('La sequenza e’ palindroma'); else disp('La sequenza NON e’ palindroma'); end !
Esercizio 5: Equazioni di secondo grado !
!
!
!
!
!
!
!
!
!
!
!
Si chieda l’inserimento dei tre coefficient di una equazione di secondo grado: ax2+bx+c=0 e si stampi il
valore delle radici reali.
Soluzione
Bisogna calcolare il discriminante dell'equazione con la formula b^2-­‐4*a*c Se è positive abbiamo due radici distinte, Se è nullo le radici sono reali e coincidenti, Se è negativo le radici non sono reali. a = input('Inserire a: '); b = input('Inserire b: '); c = input('Inserire c: '); delta = b^2-­‐4*a*c; if delta < 0 disp('L''equazione non ha soluzioni reali'); elseif delta==0 disp(['x=' num2str(-­‐b/(2*a))]); !3
!
!4
else disp(['x1=' num2str((-­‐b-­‐sqrt(delta))/(2*a)) ' x2=' ... num2str((-­‐b+sqrt(delta))/(2*a))]); !
!
Esercizio 6: Confronti
!
end Si scriva uno script che chiede di inserire una sequenza di N numeri.
Successivamente, si inserisca un ulteriore numero e si dica se tutti i numeri della sequenza sono minori,
uguali o maggiori di tale numero.
!
!
!
Soluzione
N=input('inserire N: '); for x=1:N a(x) = input('inserire numero: '); end !
!
!
!
!
M=input('inserire M: '); minori = true; maggiori = true; uguali = true; for x=1:N if a(x)>M minori=false; uguali=false; !
elseif a(x)<M maggiori=false; uguali=false; !
else maggiori=false; minori=false; end end !
!
!
!
!
!
!
if minori disp('I numeri della sequenza sono minori del numero dato'); else disp('I numeri della sequenza non sono minori del numero dato'); end if maggiori disp('I numeri della sequenza sono maggiori del numero dato'); else disp('I numeri della sequenza non sono maggiori del numero dato'); end if uguali disp('I numeri della sequenza sono uguali al numero dato'); !4
!
!
!!
!!
!
!5
else disp('I numeri della sequenza non sono uguali al numero dato'); end Versione alternativa che fa uso di operatori relazionali e vettori
N = input('inserire N: '); for x=1:N a(x) = input(['inserire numero, a(',num2str(x),')= ']); end !
!
M = input('inserire numero di confronto: '); maggiori = true; minori = true; uguali = true; !
l = length(a); if sum(a>M)== l % sono tutti maggiori di M minori = false; uguali = false; elseif sum(a<M)==l maggiori = false; uguali = false; elseif sum(a==M)==l maggiori = false; minori = false; else maggiori = false; minori = false; uguali = false; end if maggiori disp(['Tutti gli elementi di a sono maggiori di ',num2str(M)]); elseif minori disp(['Tutti gli elementi di a sono minori di ',num2str(M)]); elseif uguali disp(['Tutti gli elementi di a sono uguali a ',num2str(M)]); else disp(['Non tutti gli elementi di a sono maggiori di ',num2str(M)]); disp(['Non tutti gli elementi di a sono minori di ',num2str(M)]); disp(['Non tutti gli elementi di a sono uguali a ',num2str(M)]); end !!
Esercizio 7: Confronti con Matrici
!
Scrivere in Matlab uno script che, data una matrice m di numeri, restituisce in uscita una matrice mr,
ottenuta da m nel seguente modo: si calcola la media aritmetica dei valori di m; per i valori che in m sono
minori della media, in mr si pone nella stessa posizione il valore -1, per quelli superiori alla media si pone il
valore 1, e per gli altri (quelli uguali alla media) si pone lo stesso valore.
!
!
Si utilizzi la matrice m = [-2 2 3; 4 5 6]
Soluzione 1
!5
!
!
!
!
!6
m=[-­‐2 2 3; 4 5 6]; [R,C]= size(m); s=0; for r=1:R for c=1:C s=s+m(r,c); end end !
!
media = s/(R*C) for r=1:R for c=1:C if m(r,c)<media m(r,c)=-­‐1; !
!
elseif m(r,c)>media m(r,c)=1; end end end !
!
!
!
!
!
!
!
m Soluzione 2 m=[-­‐2 2 3; 4 5 6]; [R,C]= size(m); s=0; %utilizziamo la funzione mean media = mean(m(:)); for r=1:R for c=1:C if m(r,c)<media m(r,c)=-­‐1; elseif m(r,c)>media m(r,c)=1; end end end m
!!
!
!
!
Soluzione 3
m=[-­‐2 2 3; 4 5 6]; [R,C]= size(m); s=0; %utilizziamo la funzione mean !6
!
!
!
! !7
media = mean(m(:)); m(m<media) = -­‐1; m(m>media) = 1; m
!7