3­ congruenza.notebook
December 12, 2012
CONGRUENZA FRA FIGURE PIANE
Due figure geometriche si dicono congruenti se esiste un movimento rigido che permette di sovrapporle una con l'altra (punto per punto).
Per movimento rigido si intende un movimento di rototraslazione che non deforma la figura (questo è un concetto primitivo che quindi non viene definito!)
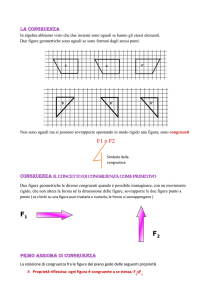
Se il movimento rigido per la sovrapposizione si svolge nel piano allora la congruenza si dice diretta (si avranno figure direttamente congruenti)
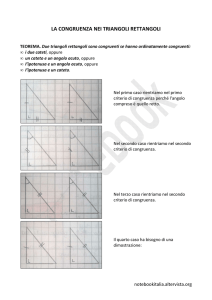
se invece per sovrapporle abbiamo bisogno di uscire dal piano allora si parlerà di congruenza inversa (figure inversamente congruenti)
Due figure si dicono uguali SOLO se sono costituite dagli stessi punti, graficamente quindi sono già sovrapposte.
1
3­ congruenza.notebook
December 12, 2012
PROPRIETA' DELLA CONGRUENZA
POSTULATO 8 (relazione di equivalenza)
­ ogni figura è congruente a se stessa: F F (proprietà riflessiva)
­ se una figura è congruente a un'altra, questa è congruente alla prima: se F1 F2 allora F2 F1 (proprietà simmetrica)
­ se due figure sono congruenti a una terza allora esse sono tutte congruenti fra loro: se F1 F2 e F2 F3 allora F1 F3 (proprietà transitiva)
POSTULATO 9
1) Tutti i punti sono congruenti fra loro
2) Tutte le rette sono congruenti fra loro
3) Tutte le semirette sono congruenti fra loro
4) Tutti i piani sono congruenti fra loro
5) Tutti i semipiani sono congruenti fra loro
(di conseguenza tutti gli angoli nulli sono congruenti fra loro, tutti gli angoli giro sono congruenti fra loro, tutti gli angoli piatti sono congruenti fra loro)
OSSERVAZIONE:
una figura NON può essere congruente ad una sua parte!
2
3­ congruenza.notebook
December 12, 2012
CONFRONTO FRA SEGMENTI
Postulato 10 (trasporto del segmento)
Dato un segmento AB e una semiretta di origine O, esiste sulla semiretta 1! punto P tale che OP AB (è possibile "trasportare" AB sulla semiretta o su un altro segmento in modo da sovrapporli anche solo parzialmente).
Confrontare due segmenti significa confrontare la sovrapposizione di uno sull'altro (basta far coincidere uno dei due estremi e vedere dove si trova l'altro).
Essi possono quindi essere:
A
B
A
A C
B
A C
B
AB<CD
D
B D
AB CD
A
B
D
A C AB>CD
B
DEFINIZIONE:
Dati due segmenti AB e CD non congruenti, si dice che AB è minore di CD (AB<CD) se AB è congruente ad una parte di CD. Si può anche dire che il segmento CD è maggiore di AB (CD>AB).
OSSERVAZIONE:
­ può valere una sola di queste relazioni (proprietà di tricotomia)
inoltre:
­ se AB<CD e CD<EF allora AB<EF (proprietà transitiva)
3
3­ congruenza.notebook
December 12, 2012
CONFRONTO FRA ANGOLI
Confrontare due angoli significa stabilire se essi hanno la stessa ampiezza o quale dei due è maggiore.
Per farlo occorre trasportare uno sull'altro in modo da sovrapporli (anche solo parzialmente): è necessario cioè sovrapporre il vertice e un lato dell'angolo.
Postulato 11 (trasporto dell'angolo)
Dato un angolo ab e una semiretta c, esiste una e una sola semiretta d, avente origine coincidente con quella di c e giacente da una parte prefissata del piano rispetto a c, tale che cd ab. Per confrontare due angoli, dopo la loro sovrapposizione, è sufficiente vedere dove si trovano i due lati non coincidenti.
Due angoli possono quindi essere:
b
b
b
a
a
a
b
d
a c
ab<cd
b d
b
a c
ab cd
d
a c
ab>cd
DEFINIZIONE:
Dati due angoli ab e cd non congruenti, si dice che ab è minore di cd (ab<cd) se ab è congruente ad una parte di cd. Si può anche dire che l'angolo cd è maggiore di ab (cd>ab).
OSSERVAZIONE:
­ può valere una sola di queste relazioni (proprietà di tricotomia)
inoltre:
­ se ab<cd e cd<ef allora ab<ef (proprietà transitiva)
4
3­ congruenza.notebook
December 12, 2012
SOMME DI SEGMENTI Si definisce somma di due segmenti AB e CD un segmento EF costituito da due segmenti adiacenti e congruenti ad AB e CD (segmento avente per estremi gli estremi non comuni dei due segmenti dati)
B
A
C
E
D
F
Se i due segmenti sono già inizialmente adiacenti allora EF=AB+CD se invece non sono adiacenti la somma si indica EF AB+CD (per costruire il segmento somma basta infatti considerare su una retta due segmenti adiacenti congruenti ai due dati).
PROPRIETA' DELLA SOMMA:
­ commutativa: AB+CD CD+AB
­ associativa: (AB+CD)+EF AB+(CD+EF)
­ elemento neutro: segmento nullo ­ somme di segmenti congruenti sono congruenti:
se AB A'B' e CD C'D' allora AB+CD A'B'+C'D'
Osservazione:
Per calcolare la differenza è sufficiente "trasformarla" in una somma: AB­CD EF allora AB CD+EF.
DEFINIZIONE:
Si dice differenza di due segmenti AB e CD (con AB>CD) un qualunque segmento EF che, sommato a CD, da il segmento congruente ad AB.
Osservazione:
La differenza di due segmenti congruenti è il segmento nullo. (La somma o la differenza di un segmento e del segmento nullo è il segmento dato)
POSTULATO 12:
Somme di segmenti rispettivamente congruenti sono congruenti, differenze di segmenti rispettivamente congruenti sono congruenti.
5
3­ congruenza.notebook
December 12, 2012
SOMME DI ANGOLI α β
Si definisce somma di due angoli e un qualunque angolo α β
costituito da due angoli consecutivi congruenti ad e (angolo avente per lati i lati non comuni dei due angoli dati)
α
β
β
α
Se i due angoli sono già inizialmente consecutivi allora α
β
= + se invece non sono già consecutivi la somma si indica β
α
+ PROPRIETA' DELLA SOMMA:
α β β α
­ commutativa: + + α β
α β
­ associativa: ( + )+ +( + )
­ elemento neutro: angolo nullo ­ somme di angoli congruenti sono congruenti
DEFINIZIONE:
α β
α β Si dice differenza di due angoli e (con > ) un qualunque β
α
angolo che, sommato a , da l'angolo congruente ad .
Osservazione:
La differenza di due angoli congruenti è l'angolo nullo. (La somma o la differenza di un angolo e dell'angolo nullo è l'angolo dato)
POSTULATO 13:
Somme di angoli rispettivamente congruenti sono congruenti, differenze di angoli rispettivamente congruenti sono congruenti.
DEFINIZIONI:
Due angoli si dicono supplementari se la loro somma è un angolo piatto (angoli adiacenti sono anche supplementari);
due angoli si dicono esplementari se la loro somma è un angolo giro.
TEOREMA:
Angoli supplementari di angoli congruenti sono congruenti;
angoli adiacenti ad angoli congruenti sono congruenti;
angoli supplementari di uno stesso angolo sono congruenti;
angoli adiacenti a uno stesso angolo sono congruenti.
6
3­ congruenza.notebook
December 12, 2012
MULTIPLI E SOTTOMULTIPLI DI SEGMENTI E DI ANGOLI
Si dice che un segmento è multiplo di un altro se il primo è congruente alla somma di n segmenti congruenti al primo.
A1
B1
A2
A3
B2
B3
A4
B4
A1B1 A2B2 A3B3 A4B4 A1B4 4 A1B1
Il segmento A1B1 sarà sottomultiplo di A1B4 Stessa definizione per gli angoli:
si dice che un angolo è multiplo di un altro se il primo è congruente alla somma di n angoli congruenti al primo.
Inoltre:
POSTULATO 14: (DIVISIBILITA' DELL'ANGOLO)
α
Dato un angolo e un numero naturale n (diverso da zero), esiste almeno un angolo tale che β
Osservazione:
se AB CD allora nAB nCD e se allora e
DEFINIZIONI:
­ Si dice che un angolo è retto se è la metà di un angolo piatto
­ Due rette che incontrandosi dividono il piano in quattro angoli retti si dicono perpendicolari (analogamente lo saranno le semirette o i segmenti)
­ Un angolo < di un angolo retto si dice acuto
­ Un angolo convesso > di un angolo retto è ottuso
­ Due angoli si dicono complementari se la loro somma è un angolo retto
TEOREMA:
Angoli complementari di uno stesso angolo o di angoli congruenti, sono congruenti.
7
3­ congruenza.notebook
December 12, 2012
PUNTO MEDIO ­ BISETTRICE ­ ASSE
Dato un segmento AB, se esiste un punto interno al segmento che lo divide in due parti congruenti, allora esso si definisce punto medio del segmento.
A
B
M
Dato un angolo aOb, con vertice in O, se esiste una semiretta c con origine in O interna all'angolo che lo divide in due parti congruenti, allora essa si definisce bisettrice dell'angolo.
c
b
O
a
Se una retta passa per il punto medio di un segmento ed è perpendicolare ad esso, allora la retta si definisce asse del segmento.
A
M
B
TEOREMI:
­ Il punto medio di un segmento esiste ed è unico.
­ La bisettrice di un angolo esiste ed è unica.
8