Geometria Razionale
Confronto di angoli e segmenti
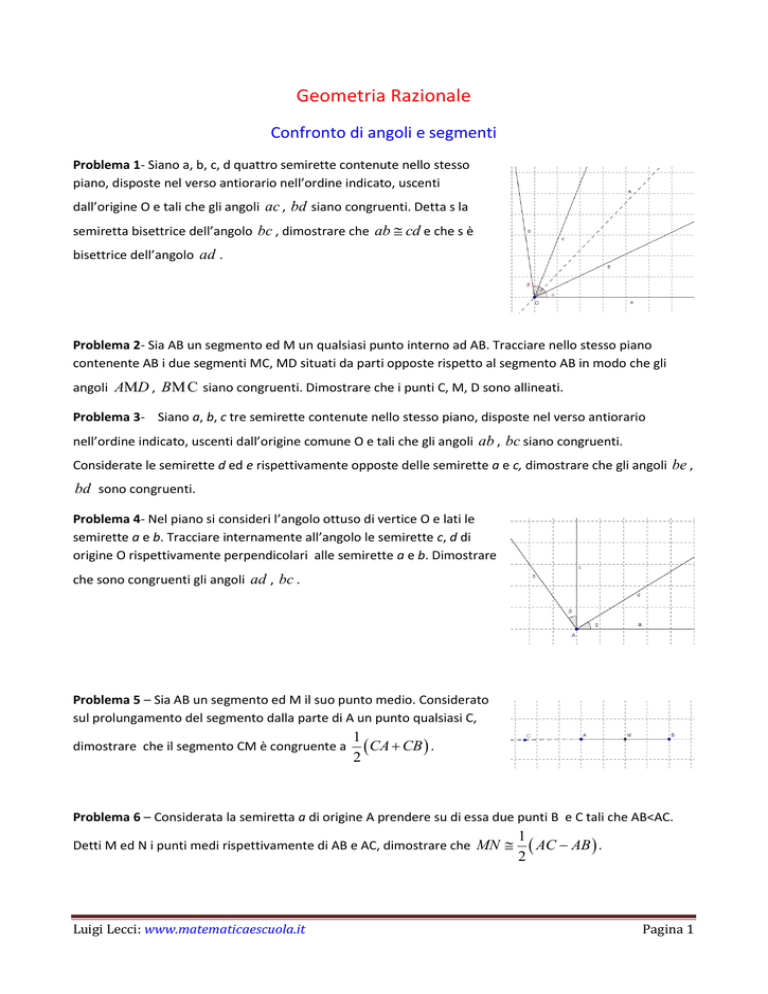
Problema 1- Siano a, b, c, d quattro semirette contenute nello stesso
piano, disposte nel verso antiorario nell’ordine indicato, uscenti
dall’origine O e tali che gli angoli ac , bd siano congruenti. Detta s la
semiretta bisettrice dell’angolo bc , dimostrare che ab cd e che s è
bisettrice dell’angolo ad .
Problema 2- Sia AB un segmento ed M un qualsiasi punto interno ad AB. Tracciare nello stesso piano
contenente AB i due segmenti MC, MD situati da parti opposte rispetto al segmento AB in modo che gli
angoli AMD , B M C siano congruenti. Dimostrare che i punti C, M, D sono allineati.
Problema 3- Siano a, b, c tre semirette contenute nello stesso piano, disposte nel verso antiorario
nell’ordine indicato, uscenti dall’origine comune O e tali che gli angoli ab , bc siano congruenti.
Considerate le semirette d ed e rispettivamente opposte delle semirette a e c, dimostrare che gli angoli be ,
bd sono congruenti.
Problema 4- Nel piano si consideri l’angolo ottuso di vertice O e lati le
semirette a e b. Tracciare internamente all’angolo le semirette c, d di
origine O rispettivamente perpendicolari alle semirette a e b. Dimostrare
che sono congruenti gli angoli ad , bc .
Problema 5 – Sia AB un segmento ed M il suo punto medio. Considerato
sul prolungamento del segmento dalla parte di A un punto qualsiasi C,
dimostrare che il segmento CM è congruente a
1
CA CB .
2
Problema 6 – Considerata la semiretta a di origine A prendere su di essa due punti B e C tali che AB<AC.
Detti M ed N i punti medi rispettivamente di AB e AC, dimostrare che MN
Luigi Lecci: www.matematicaescuola.it
1
AC AB .
2
Pagina 1












