MATEMATICA GENERALE
prof. Gianna Figà-Talamanca
Argomenti svolti durante le lezioni e le esercitazioni – a.a. 2013-2014
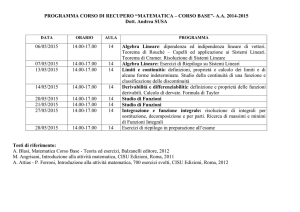
data
ore
tipo
argomento
25-09
3
L
26-09
3
L
02-10
3
L
09-10
3
L
16-10
3
L
17-10
3
L
23-10
3
L
24-10
3
L
29-10
3
SD
30-10
3
L
31-10
3
L
04-11
3
SD
29-11
SD
Presentazione e introduzione al corso. Modalità di organizzazione del corso e regole per il superamento
dell'esame. Notazioni e operazioni tra insiemi. Operazioni tra insiemi (unione intersezione, differenza). Insiemi di
numeri: i numeri naturali, interi e razionali. I numeri interi ,razionali e reali.. L'asse reale. Sottoinsiemi di R: intervalli
e semirette. Il concetto di funzione. Insieme di partenza (dominio) e di arrivo (codominio). Funzioni iniettive,
suriettive e biiettive. Immagine della funzione. Restrizioni del dominio e codominio di una funzione. Esempi.
Funzioni composte. Funzione inversa. il piano cartesiano. Il grafico di una funzione nel piano cartesiano. Le
funzioni lineari. Rappresentazione grafica e studio del segno. (le equazioni e disequazioni di primo grado.
Traslazioni verticali del grafico di una funzione lineare. Esempi.
Le funzioni quadratiche e le relative equazioni e disequazioni di secondo grado. Traslazioni orizzontali e verticali
del grafico di una funzione quadratica e di una funzione qualsiasi. Una generica funzione quadratica come traslata
di una parabola con vertice nell’origine. Esempi. La funzione valore assoluto di un numero reale. Esercizi su
traslazioni e studio del segno per funzioni quadratiche e per il valore assoluto,
Funzioni cubiche (caso particolare). Traslazioni verticali e orizzontali. Le funzioni irrazionali. La funzione radice e le
sue traslate. Equazioni e disequazioni irrazionali per lo studio del segno. Dal grafico di f(x) a quello di –f(x) , di |f(x)|
e di f(|x|). Simmetrie rispetto a un punto e rispetto a una retta. Funzioni pari e dispari. Esercizi.
Le funzioni del tipo a/x e le sue traslazioni verticali e orizzontali; Studio del segno. Rapporto di polinomi di primo
grado come traslazione di una funzione A/x (nei dettagli). Esempi di applicazione.
Esercizi su traslazioni verticali e orizzontali di funzione quadratiche, cubiche e iperboli. Studio del segno.
Rappresentazione grafica di –f(x) e di |f(x)| negli esempi proposti.
Funzioni del tipo x^a. La funzione quadratica (con opportune restrizioni del dominio) come inversa della funzione
radice. Funzioni esponenziali. Esempi. Soluzione di equazioni esponenziali. Il logaritmo e le sue proprietà. La
funzione Logaritmo. La funzione esponenziale come inversa della funzione logaritmo. Definizione di Funzioni
monotone (crescente, non decrescente, decrescente e non crescente).
Ancora sulla funzione logaritmo. Proprietà. Teoria degli insiemi: definizione di intorno di un punto; punto interno,
isolato e di accumulazione per un insieme. Maggioranti e minoranti per un sottoinsieme di R. Estremo superiore
ed inferiore di un insieme. Insieme limitato. Esempi. Funzioni limitate inferiormente, funzioni limitate
superiormente. Funzioni limitate. Limiti di una funzione. Esempi.
Definizione di un intorno di + ∞ e -∞. Ancora sui limiti di una funzione. Limite destro e limite sinistro. Esempi.
Calcolo e verifica di alcuni limiti di funzione..
Assistenza agli studenti per svolgimento Esercitazione n.1 assegnata per casa e disponibile sul sito del corso dal
28 ottobre.
Successioni. Limiti di successioni. Successioni convergenti, divergenti, indeterminate. Esempi. Successioni
geometriche e limiti. Teorema di unicità del limite, Teorema della permanenza del segno, teorema del confronto e
dei carabinieri. Teoremi su limiti di funzioni monotone e sul limite del prodotto tra due funzioni di cui una limitata e
l’altro con limite nullo. Teoremi analoghi sulle successioni. Soluzioni di alcune forme indeterminate di limite che
coinvolgono funzioni polinomiali: esempi.
Infinito e infinitesimo: definizione ed esempi. Confronto tra infiniti ed infinitesimi. Esempi illustrativi per lo
svolgimento di esercizi su prova d’esame (Rappresentazione del grafico di una funzione f come traslazione di
funzioni elementari con grafico della funzione opposta –f e della funzione composta con il valore assoluto, |f(x)| e
f(|x|) , studio di dominio, zeri e segno di alcune funzioni e calcolo dei limiti necessari a capirne l’andamento)
Assistenza agli studenti per svolgimento Esercitazione n.2 (riepilogo I parte corso) assegnata per casa e
disponibile sul sito del corso dal 2 novembre.
Definizione di funzione continua in un punto x0 del suo dominio o in un suo sottoinsieme. Continuità da destra e
da sinistra in un punto e classificazione dei vari tipo di discontinuità (salto finito, salto infinito, discontinuità
eliminabile). Esempi.
Proprietà delle funzioni continue. Teorema degli zeri (no dim), Teorema dei valori intermedi o di Darboux (con
dim.). Teorema di Weierstrass. Continuità, monotonia e invertibilità di una funzione. Derivabilità di una funzione in
un punto x0 del suo dominio. Rapporto incrementale. Algebra delle derivate (derivata prima della somma, del
prodotto, del quoziente,…). Derivata prima delle funzioni polinomiali.
Limiti notevoli utili al calcolo della derivata di funzioni elementari come exp(x), log(x) a^x. Derivata di funzioni
composte. Esempi.
Esercizi sulle derivate. Interpretazione geometrica della derivata prima. Derivata destra e sinistra di una funzione in
un punto e classificazione dei punti di non derivabilità. Punti di massimo e di minimo relativo/locale. Il Teorema di
Fermat (con dim). Test per la monotonia di una funzione.
Dimostrazione che una funzione derivabile in un punto e’ continua nel punto, Esempi di non validità del viceversa.
Il Teorema di Lagrange (no dim, ma illustrazione). Il Teorema di Rolle (con dim). Dimostrazione che una funzione
la cui derivata e’ nulla in un intervallo e’ una funzione vostante in tale intervallo (conseguenza Teo Lagrange).
Derivate di ordine superiore al I. Formula di Taylor.
Formula di Mc- Laurin. Applicazione della formula di Taylor e di Mc-Laurin per l’approssimazione di una funzione
in un punto. Insieme covesso: definizione. Epigrafico di una funzione. Funzioni convesse e funzioni concave:
definizione. Convessità/Concavità e osservazioni sulle derivate prima e seconda. Test per la convessità/concavità
di una funzione. Punti di flesso. Esempi.
Esercizi su Studi di funzione
3-12
SD
Esercizi su studi di funzione completi e formula di Taylor
13-11
14-11
20-11
21-11
27-11
28-11
4-12
Il Teorema di de L’Hospital. Applicazione al confronto di infiniti (log(x), exp(x) e funzioni polinomiali).
Cenni su funzioni a due variabili: rappresentazione grafica, sezioni del grafico e curve di livello. Derivate parziali.
Primitiva di una funzione. Dimostrazione che la differenza tra due primitive di una stessa funzione e’ una
costante. Primitiva di una combinazione lineare di funzioni. Calcolo della primitiva di funzioni elementari (x^n, x^1, x^alpha, exp(x)). Integrale indefinito. Esempi.
.
5-12
6-12
SD
Calcolo di un integrale mediante il metodo di cambiamento della variabile (sostituzione) e mediante il metodo di
integrazione per parti. Esempi. L’integrale definito e area “con segno”. Proprietà dell’integrale definito.
Definizione della Funzione Integrale di una funzione. Il Teorema di Torricelli-Barrow.
Esercizi su integrali indefiniti, studio della continuità e studi di funzione completi
10-12
SD
Esercizi su integrali indefiniti e svolgimento parziale di prove di completamento anni precedenti
SD
Il Teorema fondamentale del calcolo integrale. Esempi di calcolo per integrali definiti e Aree. Introduzione
all’algebra lineare. Vettori di R^n. Relazioni ed Operazioni tra vettori. R^n come spazio vettoriale. Sottospazi
vettoriali. Vettori linearmente indipendenti: definizione ed esempi, Generatori e base di uno spazio vettoriale.
Matrici. Relazioni e Operazioni tra matrici. Matrici simmetriche, matici diagonali, Matrice trasposta. Il prodotto
scalare tra vettori di R^n . Il prodotto matriciale (riga per colonna). Esempi di calcolo del prodotto tra matrici.
Esempi di casi in cui tale prodotto non e’ attuabile. Determinante di una matrice quadrata (nxnI.
Esercizi su integrali definiti e sul calcolo di aree, Altri esercizi di riepilogo. Esercizi base di Algebra lineare.
SD
Determinante di una matrice quadrata di dimensione 2x2 e 3x3 (Regola di Sarrus). Dipendenza/indipendenza
lineare tra n vettori di R^n e determinante. Rango di una matrice rettangolare. Esempi.
Esercizi di Algebra lineare e di Riepilogo sula II parte del programma
SD
Sistemi lineari; forma matriciale. Teorema di Rouchè Capelli. Regola di Cramer per la determinazione della
soluzione nel caso di Rango massimo=n. incognite. Sistemi omogenei.
Esercizi di Algebra lineare e di Riepilogo sula II parte del programma
11-12
12-12
13-12
16-12
17-12
18-12
20-12
Legenda
tipo
, L: lezione, SD: attività di supporto alla didattica.