La teoria dell’utilità attesa
Enrico Saltari
1
La teoria dell’utilità attesa
In un contesto di certezza esiste un legame biunivoco tra azioni e conseguenze: ad ogni azione corrisponde una e una sola conseguenza, e viceversa. Le azioni possono essere perciò ordinate sulla base dell’utilità delle
conseguenze.esempio certezza1 esempio certezza2
In un contesto di incertezza a ciascuna azione corrispondono più conseguenze. La teoria dell’utilità attesa consente di ordinare le azioni quando
vi è incertezza. esempio incertezza
Essa si fonda su due elementi:
1. la probabilità attribuita a ciascuna conseguenza xi di veri…carsi: p (xi);
2. l’utilità assegnata alle conseguenze: U (xi):
2
L’utilità attesa di un’azione è data dalla media ponderata delle utilità delle
conseguenze che discendono da quell’azione con un peso pari alla probabilità
che hanno di veri…carsi:
E [U (x)] =
X
U (xi)p(xi)
Esempio
Supponiamo che vi siano soltanto due conseguenze, x1 = 0 e x2 = 100, ciascuna
avente la stessa probabilità di veri…carsi, p1 = p2 = 12 : La funzione di utilità
p
de…nita sulle conseguenze sia u (x) = x: Allora l’utilità attesa è
E [U (x)] = p1u (x1) + p2u (x2)
1p
1p
=
0+
100 = 5
2
2
3
Il criterio dell’utilità attesa generalizza il criterio del valore atteso
E ( x) =
X
xi p ( xi )
Esempio
Come prima, supponiamo che vi siano soltanto due conseguenze, x1 = 0 e
x2 = 100, ciascuna avente la stessa probabilità di veri…carsi, p1 = p2 = 12 :
Allora il valore atteso è
E (x) = p1x1 + p2x2
1
1
=
0+
100 = 50
2
2
4
Un gioco è equo se il guadagno atteso è nullo, ovvero se il prezzo (x0) che si
paga per partecipare al gioco è pari al valore atteso che ci aspetta di ottenere
dal gioco
E ( x ) = x0
Se invece valutiamo le conseguenze in termini di utilità, e non in termini
del valore monetario, un gioco è equo se l’utilità che ricaviamo partecipando al gioco è pari all’utilità della somma che siamo disposti a pagare per
parteciparvi
E [U (x)] = U (x0)
Esempio
Come prima, supponiamo che vi siano soltanto due conseguenze, x1 = 0 e
x2 = 100, ciascuna avente la stessa probabilità di veri…carsi, p1 = p2 = 21 :
5
Allora, con il criterio dell’utilità attesa il prezzo che siamo disposti a pagare è
p
E [U (x)] = 5 = U (x0) = x0 =) x0 = 25
mentre con il criterio del valore atteso è 50.
Il paradosso di S. Pietroburgo mostra come le insu¢ cienze del criterio del
valore atteso siano dovute alla valutazione della somma in termini monetari.
Il criterio dell’utilità attesa rimuove questa insu¢ cienza valutando le somme
vinte in termini di utilità –sicché la valutazione non è più lineare nei payof f
(gli xi). L’utilità attesa continua a essere lineare nelle probabilità.
6
Lancio
Esito
1
T
2
CT
3
CCT
:::
:::
n
CC
: : : C}T
| {z
n 1
:::
:::
Probabilità
1
2
1 1
2 2
1 2 1
2
2
:::
1 n 1 1
2
2
:::
1
1
1 + + ::: = 1
2
2
P i
U tilita attesa =
ln (2) = ln (4)
2i
Somma vinta
Utilità
2
ln (2)
4
2 ln (2)
8
3 ln (2)
:::
:::
2n
n ln (2)
:::
:::
P 2i
V alore atteso =
=1
2i
7
Cosa a¤erma il teorema dell’utilità attesa
Il teorema dell’utilità attesa a¤erma che, se il comportamento individuale si conforma a certi assiomi, allora dire che un’azione o una distribuzione di probabilità
p è preferita ad un’altra distribuzione q equivale a dire che ha un’utilità attesa
maggiore
p
q ()
X
U ( xi ) p ( xi ) >
X
U ( xi ) q ( xi )
Due proprietà dell’utilità attesa
1. L’utilità attesa è additiva negli stati. L’utilità che si ottiene in uno stato non
in‡uenza l’utilità che si ottiene se si veri…ca un altro stato: l’utilità dipende
solo dalla conseguenza x che si veri…ca ma non dalle altre.
2. L’utilità attesa è lineare nelle probabilità. L’utilità attesa è una funzione
lineare delle probabilità.
8
Cosa sono p e q
Supponiamo che le distribuzioni abbiano solo due conseguenze, c1 e c2: Le
distribuzioni p e q sono
q
p
p1
p2
c1
c2
q1
q2
c1
c2
Gli assiomi dell’utilità attesa
Gli assiomi su cui si fonda la teoria dell’utilità attesa sono i seguenti:
Completezza e coerenza. Tutte le distribuzioni possono essere ordinate e in
questo ordinamento non vi è contraddizione:
p
se p
q oppure q p o entrambe;
q e q r allora p r:
9
Monotonicità. Si preferiscono le distribuzioni che assegnano le conseguenze
migliori con la probabilità più elevata:
m
(1
)
p
(1
m
)
p
se e solo se
ALF A
1
BET A
m
p
m
p
1
Continuità. Variando la probabilità assegnata alle conseguenze, mutano anche
con continuità le preferenze:
Esiste un
r
m
tale che
(1
)
p
10
Esempio
Supponiamo che p = 0 e m = 1000: Qual è la probabilità
l’individuo indi¤erente tra ottenere 250 euro con certezza, x
partecipare a un gioco in cui può ottenere 0 o 1000 euro con
1
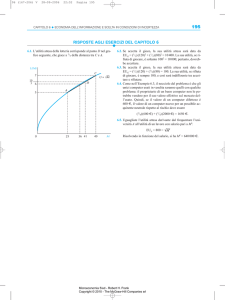
e ? Il gra…co mostra il caso di un individuo in cui questa
è 21 . Perciò, u (x) = 0:5:Formalmente,
250
0 :5
1000
0 :5
che rende
= 250; e
probabilità
probabilità
0
ovvero
u (250) = 0:5u (1000) + 0:5u (0) = 0:5;
ponendo u (1000) = 1 e u (0) = 0: Notare che il valore atteso del gioco è
500.
r
w
La funzione di utilità in questo caso è u (w) =
: La funzione ordinale
1000
p
w viene “cardinalizzata” …ssando l’origine e l’unità di misura.
11
1. Quando w = 0; anche
p
w è uguale a 0. Nessuna modi…ca è necessaria.
2. Quando w = 1000; l’utilità deve essere pari a 1. Questo viene ottenuto
normalizzando a 1 la ricchezza massima, dividendo cioè w per 1000.
1
0.8
0.6
0.4
0.2
0
125
250
375
500
625
750
875
1000
12
La funzione di utilità u (w) =
r
w
1000
13
Supponiamo invece che x = 500: Se la funzione di utilità è quella indicata
allora la probabilità che rende l’individuo indi¤erente tra avere 500 per cert
e partecipare alla lotteria è
u (500) =
s
500
= 0:707
1000
Supponiamo che un altro individuo consideri 125 euro con certezza equivalenti alla partecipazione al gioco precedente
125
0 :5
1000
0 :5
0
in termini di utilità possiamo scrivere
u (125) = 0:5u (1000) + 0:5u (0) = 0:5
e quindi u (125) = 0:5
L’individuo ritiene equivalente partecipare a un gioco il cui valore atteso è 500
o avere con certezza 125 euro: è perciò più avverso al rischio dell’individuo
prima visto.
14
w 1=3
La funzione di utilità in questo caso è u (w) =
.
1000
1
0.8
0.6
0.4
0.2
0
125
250
375
500
625
750
875
1000
w 1=3
w 1=3
(in rosso) e u (w) =
Le funzioni di utilità u (w) =
1000
1000
15
Indipendenza o sostituzione. Tra le distribuzioni di probabilità non esiste
complementarità esempio indipendenza:
p
q ()
p
(1
)
r
q
(1
)
r
Riduzione. Ai …ni del giudizio di preferenza conta soltanto la probabilità totale
assegnata alle conseguenze e non come essa si forma.
Il teorema dell’utilità attesa
Per dimostrare il teorema dell’utilità attesa, prendiamo in considerazione una
distribuzione p che prevede solo due conseguenze certe, x1 e x2 :
p = p1
x1
p2
x2
16
La dimostrazione richiede che
E [U (p1
x1
p2
x2 )]
= p1U ( x1) + p2U ( x2)
L’utilità attesa ha due proprietà: 1) è additiva nell’utilità delle conseguenze e
2) lineare nelle probabilità.
1 : Assioma di continuità. Ciascuna delle due conseguenze può essere riscritta
in termini di m (la conseguenza migliore) e p (la conseguenza peggiore)
x1
x2
U ( x1 )
U ( x2 )
m
m
(1
(1
U (x1))
U (x2))
p
p
2 : Assioma di indipendenza. Ciascuna delle conseguenze può essere sostituita
nella distribuzione originaria
p = p1
p2
x1
x2
p1 [U (x1)
(1 U (x1))
p2
m
p]
p1 [U (x1)
(1 U (x1))
m
p]
p2 [U (x2)
(1 U (x2))
m
p]
x2
17
3 : Assioma di riduzione. La distribuzione ottenuta può essere scritta in termini
delle probabilità totali di m e p
p
2
X
piU (xi)
m
1
4 : Assioma di continuità.
0
@1
2
X
1
1
piU (xi)A
p
P2
1 piU (xi) rappresenta l’utilità attribuita a p
E [U (p)] =
2
X
piU (xi)
1
5 : Assioma di monotonicità. Tra due distribuzioni viene preferita quella che
ha probabilità (utilità) più alta.
18
p1
!
U ( x1 )
!
m
x1
1
!
U ( x1 )
p
p
U ( x2 )
!
!
m
x2
p2
1
!
U ( x2 )
p
19
L’unicità della funzione di utilità
Una distinzione importante tra funzioni di utilità
1. La funzione di utilità de…nita sulle conseguenze, U (x) ;
2. La funzione di utilità riguardante le azioni, E [U (x)] :
Il teorema di unicità riguarda la prima e a¤erma che una funzione di utilità U (x)
rappresenta le preferenze sulle azioni allo stesso modo di una funzione di utilità
V (x) se e solo se fra le due esiste una relazione lineare: V (x) = a + bU (x) ,
con b > 0.
Supponiamo che l’azione p sia preferita all’azione q – Ep (U ) > Eq (U ) – e che
tra le due funzioni di utilità riguardanti le conseguenze esista una relazione lineare,
V = a + bU . Allora
Ep (V ) = Ep [a + bU ] = a + bEp (U ) > a + bEq (U ) = Eq (V )
20
Per converso, supponiamo che U e V rappresentino le preferenze sulle azioni allo
stesso modo, cioè
Ep (U ) > Eq (U ) () Ep (V ) > Eq (V )
Allora, date tre conseguenze
x
y
z
per l’assioma di continuità
y
x
(1
)
z
In termini di utilità U e V
U (y ) =
U (x) + (1
) U (z )
V (y ) =
V (x) + (1
) V (z )
(1)
Ricavando
U (y )
=
U ( x)
U (z )
V (y )
=
V ( x)
U (z )
V (z )
V (z )
21
si vede che
V ( x) V ( z )
(U (y )
U ( x) U ( z )
= a + bU (y )
V (y ) =
U (z )) + V (z )
V
X
Z
Y
X-Z
α(X-Z)
U
22
Perché tra U (:) e V (:) esiste una relazione lineare
Nel gra…co il vettore y è costituito dalla combinazione lineare degli altri due vettori
y=z+
(x
z ) = x + (1
)z
Questa è l’equazione della retta, scritta in forma vettpriale, che passa per i punti z
e x:Si noti che nel gra…co il vettore y ha coordinate (U (y ) ; V (y )) : Le coordinate
dei vettori x e z vanno intese in modo analogo. Se scriviamo per esteso il vettore
y come somma degli altri due vettori, otteniamo il sistema di equazioni (1).
Esempio
Un individuo a¤erma di scegliere le proprie azioni massimizzando la seguente
funzione
E (V ) = (1 + y1)
1
(1 + y2)
2
23
Possiamo considerarlo un individuo che massimizza l’utilità attesa?
Poiché la scelta riguarda le azioni e non le conseguenze, possiamo adottare una
trasformazione non lineare di E (V ) : Prendendo i logaritmi di ambo i lati, si ha
1 ln (1 + y1 ) +
2 ln (1 + y2 )
che ha le caratteristiche tipiche (additività, linearità nelle probabilità) dell’utilità
attesa.
24
La scelta in condizioni di certezza
A ogni azione corrisponde una e una sola conseguenza.
Esempio
a ! c = F (a )
25
Insieme delle decisioni
a2
Insieme delle conseguenze
c(a 2)
c(a 3)
a3
a1
c(a 1)
Esempio
(l ) = p f (l ) w l
p
= p l w l , p = 2; w = 1
26
Insieme delle decisioni
11=1
12=4
Insieme delle conseguenze
π(l 1)=1
π(l 2)=0
indietro
27
La scelta in condizioni di incertezza
A ogni azione corrispondono più conseguenze. Di qui le di¢ coltà di ordinamento in base alle funzioni di utilità tradizionali.
Esempio
(a; s) ! c = F (a; s)
28
Insieme delle conseguenze
Insieme delle decisioni
s2
a1
s1
a2
c(a 1,s2)
s2
c(a 2,s 2)
c(a 1,s 1)
s1
c(a 2,s1)
29
Esempio: Incertezza e pro…tto
L’esempio che segue mostra nell’ambito della teoria dell’impresa che, in presenza
di incertezza, il pro…tto non dipende solo dalle azioni poste in atto, il lavoro
impiegato, ma anche dallo stato del mondo, nell’esempio dal valore dello shock,
che si veri…ca.
2 stati: s1 = cattivo tempo; s2 = bel tempo: In‡uenzano il prodotto attraverso
un disturbo moltiplicativo.
(l; s) = p f (s; l) w l
p
= p s ( l w l , p = 2; w = 1;
p
p
lp
, s = s1
s l
2
l , s = s2
Prendiamo in considerazione quattro valori possibili del pro…tto corrispondenti ai
due livelli di impiego di lavoro (1 e 4) che massimizzano il pro…tto per i due valori
dello shock (1 e 2). E’ importante osservare che non esiste il livello ottimo di
impiego di lavoro, perché il pro…tto dipende anche dallo shock. Per esempio, se
30
s = 1 conviene impiegare una quantità di lavoro pari a 1 (perché (1; 1) = 1)
e non a 4 (perché (4; 1) = 0). Viceversa, se s = 2 conviene impiegare una
quantità di lavoro pari a 4 (perché (4; 2) = 4) e non a 1 (perché (1; 2) = 3).
Il gra…co successivo illustra l’andamento del pro…tto per tutti i valori di L e s.
Alle stessi conclusioni si giunge se guardiamo all’uguaglianza tra prodotto mar-
31
d
f (L) = 21
ginale del lavoro (indicato con
dL
w
(s = 1; 2) e salario reale ( = 0:5).
p
l
1
2)
nei due stati del mondo
Non esiste perciò, come invece accade nel caso di certezza, un impiego ottimale
di lavoro indipendentemente dallo stato del mondo.
32
Insieme delle conseguenze
Insieme delle decisioni
π(s 2,l2)=4
s2
11=1
π(s 2,l1)=3
s2
s1
π(s 1,l1)=1
12=4
s1
π(s 1,l2)=0
indietro
33
Due modi di guardare all’utilità attesa
1. Come scelta tra conseguenze che dipendono dallo stato,
c = F (a; s) :
Scegliendo un’azione, si sceglie una conseguenza per ciascuno stato del mondo. La
conseguenza c viene interpretata come una variabile casuale, le cui realizzazioni
sono “stato–contingenti”. L’utilità attesa è una funzione di utilità de…nita sui
consumi contingenti
E [U (c)] = E [U (c1; c2;
; cn)]
.Nell’esempio della tabella, si sceglie tra due variabili casuali:
c1 =
c (a 1 ; s 1 ) ;
c (a 1 ; s 2 )
a1
a2
e c2 =
s1
c (a 1 ; s 1 )
c (a 2 ; s 1 )
c (a 2 ; s 1 )
c (a 2 ; s 2 )
:
s2
c (a 1 ; s 2 )
c (a 2 ; s 2 )
34
Insieme delle decisioni
bene nello
stato 2
Insieme delle conseguenze
c(a 1,s 2)
a1
c(a 2,s 2)
a2
c(a 1,s 1)
c(a 2,s 1)
bene nello
stato 1
2. Come scelta tra distribuzioni di probabilità
Le conseguenze sono variabili casuali de…nite in questo caso da distribuzioni di
probabilità. Scegliendo un’azione, l’individuo sceglie in e¤etti una distribuzione
35
di probabilità. L’utilità attesa è una funzione di utilità de…nita sulle probabilità.
E [U (p)] = E [U (p1; p2;
; pn)]
Il postulato di indipendenza a¤erma che è possibile ordinare le distribuzioni secondo le preferenze guardando alle singole parti che le compongono. Il giudizio
dipende solo dalle parti delle distribuzioni che sono diverse.
Esempio
Supponiamo che le distribuzioni abbiano solo due conseguenze, c1 e c2: Se p e q
sono valutate allo stesso modo dal consumatore
q
p
p
q () p1
p2
c1
c2
q1
q2
c1
c2
r è un’altra distribuzione de…nita in modo analogo. Allora per l’assioma di indipendenza le due distribuzioni che si ottengono combinando p e r da una parte
36
e q e r dall’altra sono anch’esse indi¤erenti.
p
p1 + (1
p2 + (1
(1
) r1
) r2
)
c1
c2
r
q
(1
q1 + (1
q2 + (1
)
r
) r1
) r1
c1
c2
Il postulato di indipendenza garantisce inoltre che le curve di indi¤erenza
siano delle rette parallele nello spazio delle probabilità.
Esempio. Supponendo vi siano solo tre conseguenze (il supporto delle distribuzioni è costituito solo da tre conseguenze), si ha
E (U ) = p1U1 + p2U2 + p3U3; con U1 < U2 < U3
Poiché p2 = 1 p1 p3; possiamo scrivere l’equazione di una curva di indi¤erenza,
con E (U ) = k; come
E (U ) = k = (U1
U2) p1 + (U3
U2) p3 + U2
37
da cui
k
p3 =
U3
U2
U2
U1
U3
U2
p1
U2
p3
1
curva di indifferenza
uti
lità
cre
sce
nte
1
p1
Le curve di indi¤erenza sono delle rette perché, dall’assioma di indipendenza, ogni
distribuzione che si trova sul segmento che congiunge p con q , come 12 p 21 q ,
deve essere ritenuta indi¤erente.
38
p
1
q ()
2
1
2
p
q
1
2
1
2
q
q=q
p3
1
½·p+½·q
q
p
1
p1
39
p3
1
¼·p+¾ ·r
¼·q+¾·r
r
q
p
1 p1
Le curve di indi¤erenza sono parallele perché, dall’assioma di indipendenza, ogni
distribuzione che si trova sul segmento che congiunge r con p o con q , come
1 p
1 q , deve essere ritenuta indi¤erente.
2
2
p
q ()
1
4
p
3
4
r
1
4
q
3
4
r
40
Il paradosso di Allais
Nel gioco proposto da Allais vi sono solo tre premi (conseguenze)
1 Premio
5 ml.
2 Premio
1 ml.
3 Premio
0 ml.
Il gioco consiste in una scelta e¤ettuata in due stadi.
I Stadio. La scelta viene e¤ettuata tra le due distribuzioni a e b; de…nite come
b
a
1ml. 1
5ml.
1ml.
0ml.
0.1
0.89
0.01
Dobbiamo cioè scegliere tra 1 milione per certo e 1 milione all’89% e 5 milioni al
10%. Quale scegliamo?
41
II Stadio. La scelta viene e¤ettuata tra le due distribuzioni c e d; de…nite come
c
1ml.
0ml.
0.11
0.89
d
5ml. 0.1
0ml. 0.9
Dobbiamo cioè scegliere tra 1 milione all’11% e 5 milioni al10%. Quale scegliamo?
Molti esperimenti mostrano che si sceglie l’opzione a nel primo caso (per non
rischiare con l’1% di probabilità di non ottenere nulla). Si sceglie invece l’opzione
d nel secondo caso perché si ritiene che non c’è grande di¤renza tra il 10 e l’11%,
e ovviamente si preferisce avere la possibilità di avere 5 milioni piuttosto che 1.
Secondo gli assiomi dell’utilità attesa questa scelta non è razionale. Le due scelte
sono infatti identiche: la prima corrisponde alla seconda aumentata dell’89% di
avere 1 milione in entrambe le opzioni.
42
Un’altra rappresentazione delle distribuzioni nel paradosso di Allais
a
b
c
d
0
1
0
1
0
1
10
1
5
1
5
11
99
1
1
0
0
Se poniamo i tre premi come esiti di una distribuzione di probabilità, x1 = 0;
x2 = 1 e x3 = 5; allora le distribuzioni possono essere rappresentate come vettori
p1 p2 p3 nel triangolo di Machina: a = 0 1 0 ; b = 0:01 0:89 0:1
c=
0:89 0:11 0
;d=
;
0:9 0 0:1
Le quattro distribuzioni sono rappresentate nella …gura seguente.
43
p3
1
curve d'indifferenza
0.1
d
b
c
a 0.01
0.9
1
p1
Si noti che se a viene preferito a b (come nella …gura), allora per il postulato di
indipendenza c è preferito a d (vedi ancora la …gura): Una dimostrazione formale
44
è la seguente
a
b ()
U (1) > 0:1U (5) + 0:89U (1) +
+0:01U (0)
0:11U (1) > 0:1U (5) + 0:01U (0) =
0:1U (5) +
+ (0:9
0:89) U (0)
0:11U (1) + 0:89U (0) > 0:1U (5) + 0:9U (0) ()
c
d
Tre tipi di reazioni al paradosso di Allais
1. (Savage) Normativa: gli errori vengono corretti.
2. Teoria del rimpianto (Regret T heory ). Si sceglie a rispetto a b perché
altrimenti si rimpiangerebbe la possibilità di aver tralasciato una vincita certa
di 1ml.
45
3. (Machina) Teoria del disappunto. Si consideri la seguente struttura delle
preferenze.
Viaggio a Venezia
Film su Venezia
Stare a casa
Se con queste preferenze ci viene proposto di scegliere tra un gioco in cui
si può avere il viaggio a Venezia con il 99% di probabilità oppure guardare
un …lm su Venezia con l’1% di probabilità e un gioco in cui si può avere
il viaggio a Venezia con il 99% di probabilità oppure stare a casa con l’1%
di probabilità, la scelta cade sul primo gioco se si rispetta il postulato di
indipendenza. Ma non è detto che questo sia l’esito se ci si aspetta che nel
caso non si ottenga il viaggio a Venezia i gusti cambieranno: il disappunto
di non aver ottenuto il viaggio a Venezia potrebbe essere tale da generare il
ri…uto di guardare un …lm su Venezia.
Sia nella teoria del rimpianto che quella del disappunto danno luogo a complementarità perché si preoccupano di ciò che sarebbe potuto accadere.
46