ECONOMICS
LA NOZIONE DI "BENI I N D I P E N D E N T I " IN BASE AI
NUOVI CONCETTI P E R LA MISURA DELLA
"UTILITÀ"
BRUNO DE FINETTI
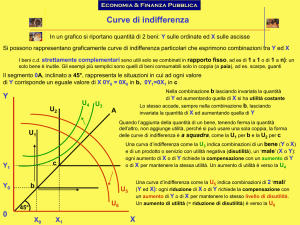
Il confronto di "preferibilità" tra situazioni economiche non può che condurre a definire linee o varietà d'indifferenza, e quindi "indici di utilità", ma
non ad attribuire a uno di essi il ruolo privilegiato di "misura dell'utilità"; a
tale nozione, che sembrava perciò doversi definitivamente abbandonare, si
ritorna invece, dandole un senso ineccepibile, qualora si ricorra alla considerazione della "preferibilità" nel campo ampliato delle "distribuzioni di probabilità fra situazioni economiche". Tale concetto, introdotto da J. von Neumann e
0 . Morgenstern, Theory of games and economic behaviour, è stato esposto e
tradotto in forma assiomatica nel modo più sodisfacente e convincente da J.
Marschak, Rationality, uncertainty, utility, Econometrica voi. 18 (2) Apr. 1950.
Strettamente legata alla misurabilità dell' utilità è la nozione di "indipendenza" dei beni: nella mia nota Sui campi di ofelimità, Rivista Ital. Se. Economiche voi. 7 (4) Lug. 1935, avevo notato che l'usuale condizione non è invariante
rispetto alla scelta dell'indice di utilità, cosicché aveva senso soltanto una
condizione più debole (di "pseudoindipendenza"), cioè la condizione per l'esistenza di un indice sodisfacente la condizione di indipendenza. Tale condizione
più debole consiste nel fatto che le linee d'indifferenza sodisfino un 'equazione
differenziale a variabili separabili, o, in forma finita, che ogni rettangolo ABCD
(lati paralleli agli assi), coi vertici A, B, C su tre linee d'indifferenza a, b, e,
abbia anche il quarto vertice D sempre su una stessa linea d'indifferenza d.
Adottando il nuovo punto di vista (Neumann-Morgenstern), la nozione di
indipendenza acquista un significato univoco. Alla precedente condizione geometrica va aggiunta una condizione stocastica dipendente dalla scelta dell'indice
d'utilità determinata dalla considerazione delle distribuzioni di probabilità.
Tale nuova condizione può essere espressa in più forme.
Localmente, come condizione differenziale, si tratta di confrontare il grado di
convessità relativa (—ff/f)
risultante dalle considerazioni stocastiche, con
quello richiesto per l'indipendenza in base alle condizioni geometriche. Il primo
si può esprimere p. es. come limite per h —> 0 di h2/2g(h), ove g(h) sia la perdita
certa indifferente con il rischio di un guadagno o perdita db/& con probabilità
1/2 e 1/2. Il secondo dipende dalla pendenza e curvatura delle linee d'indifferenza e loro traiettorie ortogonali, e vale precisamente Ki + Kn(l — q)/q
(Ki e Kn curvature dette, q pendenza).
Globalmente, in forma finita, la condizione si esprime facilmente ed espressivamente considerando quattro situazioni (xi, yì), (xi, y2), (x2, yi), (x2, y2) (x, y
588
ECONOMICS
589
quantità dei due beni considerati) ; in un campo G si ha indipendenza se è indifferente avere il diritto con probabilità 1/2 e 1/2 alla prima o l'ultima oppure
alle due intermedie fra tali quattro situazioni.
Una trattazione più dettagliata è in preparazione per il "Giornale degli
economisti".
UNIVERSITY OF
TRIESTE.
TRIESTE,
SECTION V
MATHEMATICAL PHYSICS AND APPLIED
MATHEMATICS