Quaderni di CabriRRSAE 8 - Dipartimento di Matematica e Informatica

Quaderni di CABRIRRSAE
Maura Brambilla
Enrico Lamanna
Cabri-géomètre
e i luoghi geometrici
Schede di laboratorio
N° 8
Questo lavoro è stato presentato il 12/5/1995 ad Osimo (AN)
in occasione di una giornata di aggiornamento sul software Cabri-géomètre,
organizzato dall’I.R.R.S.A.E. Marche
Maura Brambilla
insegna Matematica al Liceo Classico V. Emanuele II di Jesi
ed Enrico Lamanna
è docente di Matematica all’I.T.C.G. “F. Corridoni” di Osimo
Stampato a cura dell’I.R.R.S.A.E. – Emilia-Romagna, ottobre 1995
ESEMPI DELL'USO DI CABRI PER LA COSTRUZIONE DI PARTICOLARI LUOGHI
GEOMETRICI E SUO USO COME STRUMENTO "MATEMATICO"
Quando si approfondisce lo studio di Cabri e lo si impiega in
situazioni sempre più complesse, si scoprono le sue potenzialità
di utilizzazione e soprattutto di visualizzazione di situazioni
che sulla carta si possono solo immaginare o ricostruire con calcoli abbastanza complicati. Questo software può talvolta sostituire strumenti "matematici" che sono di difficile reperimento.
Nel seguito della trattazione vengono forniti esempi che possono
ritenersi utili da una parte e curiosi da un'altra e che comunque
si collegano direttamente alla storia della matematica.
Il primo esempio molto semplice riguarda uno strumento costruito per risolvere il problema della trisezione dell'angolo.
Si consideri il seguente enunciato: « .."Si prolunghi la corda AB
di una circonferenza di centro O di un segmento BC=OB e se E è
l'intersezione del prolungamento di CO con la circonferenza, dimostrare che l'angolo EOA è il triplo dell'angolo ECA."
Questo teorema sta alla base del trisettore di Pascal, mostrato
nella figura seguente:
Lo strumento serve per costruire il sottomultiplo secondo 3 di un
qualsiasi angolo.
Sull'asta PB è incernierata in A una seconda
asta AO, in modo che AO = AP. Una terza asta, di lunghezza eguale
alla precedente è incernierata in 0 e fissata all'asta PA con uno
snodo, che scorre entro un'apposita scanalatura. Sulla figura, dove sono riportate le ampiezze degli angoli, risulta evidente che
l'angolo BOC è tre volte l'angolo BPC.» 1
___________________
1
L. Benaglia - La Matematica,
pag. 382 - Morano Editore
i
suoi
1
metodi
e
i
suoi
problemi
-
vol.1
Nella figura seguente vi è riportata la costruzione fatta con
Cabri le cui fasi principali sono:
1. Creazione retta per due punti
2. Edizione nomi (P, C)
3. Creazione retta per due punti(P) e uno ÏPC
4. Costruzione punto su un oggetto
5. Edizione nomi (A)
6. Creazione circonferenza Centro (A)- punto (P)
7. Costruzione intersezione tra due oggetti: circonf.- Retta PC
8. Edizione nomi (O)
9. Creazione circonferenza Centro (O)- punto (A)
10.Costruzione intersezione tra due oggetti: circonf.- Retta PA
11.Edizione nomi (B)
12.Diversi angolo (per evidenziare gli angoli che interessano)
13.Diversi misura (degli angoli)
Il secondo esempio che viene trattato è quello presentato da
Descartes per il tracciamento di curve:
« ... Al ruotare del regolo YX le squadre che hanno i loro vertici
in C, D, E, F, G scorrono sui regoli YZ ed YX, in modo che gli angoli nei punti nominati siano sempre retti.
Allora i punti B, D, F, H descrivono delle curve; il punto B una
circonferenza che ha come raggio il segmento YB; gli altri descrivono delle curve che sono rappresentate, in coordinate cartesiane,
da equazioni di grado superiore al secondo.... » 1
___________________
1
L. Benaglia - La Matematica,
pag. 499-500 - Morano Editore
i
suoi
2
metodi
e
i
suoi
problemi
-
vol.2
Di seguito viene riportata l’immagine della costruzione fatta con
Cabri in cui intervengono soprattutto le opzioni Costruzioni- rette perpendicolari- e Costruzione - intersezioni di due oggetti.
Di seguito usando l'opzione Costruzione luogo geometrico, tenendo
premuto il tasto SHIFT e cliccando con il mouse sopra i diversi
punti colorati (B, D, F, H) e usando poi il punto esterno ai precedenti (X) per muovere la retta in senso circolare con perno in
Y, si ottengono i luoghi geometrici generati dai punti considerati
B, D, F e H.
Il terzo esempio riguarda un luogo geometrico la cui costruzione poi può essere verificata immediatamente con Cabri. Si ottiene così il doppio scopo della rigorosa dimostrazione geometrica
da una parte e la verifica formale della esattezza di quanto fatto
dall'altra.
«Il luogo geometrico dei punti del piano, per cui è costante il
rapporto K delle distanze da due punti B e C assegnati nel piano,
è la circonferenza il cui diametro ha per estremi i due punti che
dividono internamente ed esternamente il segmento BC nel rapporto
K assegnato. Tale luogo geometrico, per K diverso da 1, prende il
nome di CIRCONFERENZA DI APOLLONIO.» 1
Il diametro della circonferenza di Apollonio ha come estremi rispettivamente le intersezioni P e Q tra le bisettrici dell'angolo
interno ed esterno BAC con la retta contenente BC, ove A individua
il punto che determina il luogo. Nel caso in cui K=1 il triangolo
individuato dai punti BC e dal punto A, che determina il luogo, è
isoscele sulla base BC (la bisettrice dell’angolo interno BAC è
perpendicolare a BC, mentre la bisettrice dell'angolo esterno risulta parallela a BC) e pertanto si ha un problema degenere.
Tale luogo può essere ricavato con Cabri mediante l'uso del Teorema di Talete. Per primo bisogna determinare il punto P interno al
segmento BC che divide lo stesso nel rapporto K richiesto, poi il
vertice dell'angolo BAC.
Per meglio comprendere il tutto facciamo riferimento alla seguente
figura 2 che è stata opportunamente modificata in Cabri:
___________________
1
L. Benaglia - La Matematica,
pag. 176-178 - Morano Edìtore
2
idem vol.2 pag. 226
i
suoi
3
metodi
e
i
suoi
problemi
vol.
2
La prima fase della costruzione con Cabri avviene assegnando un
segmento BC e due segmenti m, n in modo tale che risulti:
BP/PC = m/n = K (¹¹1).
In Cabri è conveniente, se possibile, tenere separati gli elementi
che possano modificare le figure. Nel nostro caso i tre segmenti
assegnati saranno evidenziati per poterli modificare nella maniera
più semplice possibile, pertanto da questo momento il segmento BC
sulla costruzione verrà indicato con B’C’.
Si prende per B’ una retta qualsiasi distinta da B’C’ sulla quale
si riporta il segmento m a partire sempre dal punto B’ e che ha
come secondo estremo il punto M, quindi si traccia per C’ una retta parallela alla precedente sulla quale si riporta, sempre a partire da C’ in ambedue le direzioni il segmento n, che avrà come
estremi N ed N’. Si tracciano, infine, le rette che congiungono M
con N ed N’ che intersecano la retta passante per B’C’ nei punti P
e Q. I punti così ottenuti sono gli estremi del diametro della
circonferenza di Apollonio. Il punto P appartiene alla bisettrice
dell'angolo interno B’AC’, mentre Q appartiene alla bisettrice
dell'angolo esterno, la esattezza della costruzione è assicurata
dalla corrispondenza centrale di Talete.
Per quanto riguarda la seconda fase si fa riferimento alla seguente figura:
4
Essa nasce dal presupposto che il punto P appartenga alla bisettrice dell'angolo interno B’AC’ e pertanto il segmento B’C’ rimane
diviso in due parti direttamente proporzionali ai lati dell’angolo
B’A e C’A, percui è possibile calcolarsi il vertice A come intersezione dei segmenti B’A e C’A.
Per prima cosa si costruisce a partire da B’ una retta non coincidente con B’C’ e sulla quale si fissa un punto U la cui distanza
da B’ rappresenta il lato B’A, poi si trasla con primo estremo in
B’ il segmento PC’. A questo punto si traccia la retta passante
per P e U, poi si traccia la retta parallela a PU passante per il
secondo estremo V del segmento PC’ traslato, e si determina la sua
intersezione T con la retta B’U. Il segmento che ha come estremi
B’ e T rappresenta il secondo lato dell'angolo B’AC’. La fondatezza della costruzione è basata sul Teorema di Talete.
A questo punto la costruzione è praticamente completata, basta riportare il secondo lato in modo che abbia un estremo coincidente
con il punto C’ e tracciare le due circonferenze di centri, rispettivamente, B’ e C’ aventi come raggi i segmenti B’U e B’T.
I punti di intersezione rappresentano i vertici A degli angoli
B’AC’. Utilizzando l'opzione "Luogo geometrico" si vedrà che il
luogo geometrico descritto dal punto A al variare di U è proprio
la circonferenza avente come diametro il segmento PQ.
La costruzione completa, eseguita con Cabri, appare nella seguente
immagine :
5
CABRI E IL SUO USO IN CLASSE
Cabri può essere usato con il massimo prof itto dopo un approccio
teorico con l'argomento che si sta trattando.
Vengono riportati di seguito due esempi di percorsi didattici che
prevedono l'uso contemporaneo del foglio di carta (schede delle
attività) e del software per visualizzare, scoprire o verificare
le proprietà della figura geometrica.
A sostegno di questo tipo di approccio viene di seguito riportato
uno stralcio dell'articolo:
Organizzazione della classe per l'uso di Cabri-Géomètre
di Bernard Capponi e Colette Laborde
DidaTech, Université Joseph Fourier
1
« Gli insegnanti sanno che l'uso in classe di un programma, anche
se è promettente per la novità dei rapporti con la matematica che
permette di instaurare, ha tuttavia bisogno di organizzazione del
lavoro in classe. L’interesse di Cabri-Géomètre sta nella sua interfaccía piacevole e che consente una rapida famílíarízzazione.
....... .... L'esperienza di molti anni d'uso di Cabri-Géomètre da
parte degli insegnanti di matematica ha evídenzíato diverse forme
possibili d’organizzazione per la classe, che dipendono sia dal
numero di computer disponibili, sia dal tipo d'attività.
...........
Lavoro di gruppo Se si dispone di più computer, gli alunni possono
essere divisi in gruppi, uno per macchina. Il numero che risulta
essere il più proficuo è di due alunni per macchina. Affinché i
ragazzi lavorino in modo autonomo, è importante che essi dispongano di una scheda contenente il compito da svolgere e la descrizione delle fasi del lavoro. Altrimenti, non potendo rispondere simultaneamente a tutte le domande (diverse) dei vari gruppi,
l'insegnante sarebbe obbligato a fare interventi collettivi che
riguarderebbero una sola parte della classe e disturberebbero gli
altri. Se gli alunni dispongono di schede che forniscono í dati e
l'obiettivo dell'esercizio, l'insegnante si limita a passare da un
gruppo all'altro per osservare come procede il lavoro degli alunni
e rispondere eventualmente a domande di tipo tecnico.
A questa fase di lavoro autonomo degli alunni deve far seguito una
fase collettiva nella quale sono presentate e discusse le decisioni e le soluzioni di ogni gruppo. E' importante che la fase di lavoro autonomo sbocchi in questa fase collettiva che permette di
rendere omogenee le conoscenze della classe e di formalizzare gli
elementi importanti della soluzione.
In effetti occorre notare che, essendo un ambiente aperto, Cabri
permette in generale una grande diversità di soluzioni.
___________________
1
Bollettino CABRIRRSAE
Emilia Romagna
numero
4
Febbraio
6
95
pag
2-3
edito
dall'IRRSAE
D’altra parte, come è stato spesso rilevato, -i ragazzi provano un
gran numero di percorsi permessi dal computer, anche se non hanno
in testa una strategia decisa. ...........
Poiché il computer favorisce l'azione a spese della formulazione,
è interessante chiedere aglí alunni una soluzione scritta, fín
dalla fase del lavoro autonomo. Può essere ad esempio la giustificazione delle costruzioni realizzate con Cabri. ..........»
ESEMPIO n° 1 PARABOLA
Obiettivo di questo esempio è la costruzione della parabola vista
attraverso la sua definizione di luogo geometrico che deve essere
scoperta passo passo dagli studenti e successivamente verificata
con una costruzione fatta con Cabri. Un successivo passo è la rappresentazione della parabola in un sistema di assi cartesiani ortogonali in cui viene fatta la costruzione della equazione che la
rappresenta per via geometrica mediante l'uso del teorema di Talete.
DESTINATARI: Alunni del 2 o 3 anno di una scuola media superiore.
TEMPO: 3 ore.
PREREQUISITI: Geometria euclidea (fino al teorema di Talete).
Elementi base di geometria analitica.
7
A) DISEGNARE LA PARABOLA CON CABRI COME LUOGO GEOMETRICO
A.1 Costruzione della conica come luogo geometrico
ATTIVITÁ 1 Definizione della parabola come luogo geometrico
OBIETTIVO
riflettere sulla condizione analitica che caratterizza il luogo geometrico
Scrivi la definizione di parabola come luogo:
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
Completa la seguente f igura individuando con una buona precisione due punti (P e Q distinti) che appartengano al luogo
FIG 1
Rifletti:
Dalla definizione e dalla figura precedente puoi affermare che:
per ogni punto del luogo esiste una relazione che caratterizza il
luogo:
- descrivila:
__________________________________________________________________
__________________________________________________________________
- traducila in simboli matematici
__________________________________________________________________
8
ATTIVITÁ 2 Costruzione teorica e geometrica del luogo
OBIETTIVO
definire, sul foglio, la costruzione geometrica
rigorosa di un generico punto del luogo
1) Con riferimento all'attività 1, per il punto P o per Q , osserva che:
il segmento FP è la ______________di ___ da ___, il segmento PH è
la _____________ di _____ dalla retta _____ .
2) I segmenti FP e PH sono quindi lati di un triangolo ___________
i cui vertici sono _____________________________
3) Osserva la figura seguente:
FIG 2
4) Esiste una simmetria che faccia corrispondere FP a PH determina
l'asse __________________________;
in questa simmetria il punto P è punto __________________________
5) Rifletti:
L'asse di simmetria ora determinato è ____________ del segmento FH
quindi il punto P è anche intersezione delle rette _____________ e
__________________________________________________________________
6) Concludi: dati il punto F e la retta r, la procedura più rapida
per disegnare sul foglio un generico punto P del luogo (parabola)
basta ...
__________________________________________________________________
__________________________________________________________________
9
ATTIVITÁ 3 Realizzazione del disegno con Cabri
OBIETTIVO:
Disegnare l'intero luogo geometrico - la parabola
- con Cabri
1) Apri un nuovo foglio.
2) Creazione - retta per due punti (direttrice)
3) Creazione - punto F (fuoco)
4) Scrivi i comandi per individuare il punto P in base a quanto
affermato nei punti 5) e 6) dell'attività precedente.
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
5) attiva l'opzione "luogo geometrico" individuando in P il punto
di cui si vuole la traccia al variare di H sulla direttrice
6) salva la figura (PARABOLA).
PER LA SOLUZIONE VEDI APPENDICE 2 FIGURA 1
A.2 Studio delle caratteristiche dei luogo geometrico (parabola)
ATTIVITÁ 4 Inserimento nel piano cartesiano
OBIETTIVO:
riferire il luogo precedente ad un sistema di assi cartesiani.
E' possibile riferire la costruzione precedente ad un sistema di
assi cartesiani.
1) Apri un nuovo foglio
2) Crea due rette perpendicolari (gli assi cartesiani) chiamando o
in punto intersezione.
3) Ripeti la costruzione ' della parabola scegliendo come fuoco un
punto F che appartiene alleasse Y e come direttrice d una parallela all’asse X. PER LA SOLUZIONE VEDI APPENDICE 2 FIGURA 2
4) Rifletti:
come sceglieresti F e d in modo che la parabola abbia vertice in
O?
__________________________________________________________________
ATTIVITÁ 5 Variazione di parametri e osservazioni sulla figura
OBIETTIVO:
Studio del legame tra parametri definitori del
luogo e forma del luogo stesso.
1) Costruisci una parabola che abbia:
a - asse di simmetria parallelo alleasse Y o alleasse X
b - stesso asse e passi per O (con O diverso da V)
c - con la concavità rivolta verso il basso
2) Come devi variare i parametri per ottenere una parabola più
(o meno) aperta ?
__________________________________________________________________
10
B)DISEGNA LA PARABOLA CON CABRI IN UN SISTEM DI ASSI
CARTESIANI USANDO IL TEOREMA DI TALETE
B.1 Costruzione della conica con altro metodo e confronti tra le due modalità
2
ATTIVITÁ 1 Costruzione della parabola y=X con Talete
OBIETTIVO:
Ottenere la costruzione della parabola utilizzando il teorema di Talete
E' possibile costruire la parabola in altro modo utilizzando il
teorema di Talete: infatti sfruttando degli opportuni segmenti
proporzionali è possibile ottenere un segmento che risulta essere
il quadrato di X. Con una ulteriore applicazione dello stesso teorema è possibile tracciare la parabola di equazione y = aX2 con
concavità rivolta verso l'alto se a > 0 e viceversa se a < o
1) Apri un nuovo foglio
2) Crea due rette perpendicolari (gli assi cartesiani) chiamando 0
il punto intersezione.
3) Determina due punti appartenenti alleasse x che chiami con 1
(segmento unitario) ed x
4) Costruisci la circonferenza dì centro O e raggio 1 determinando
le ulteriori intersezioni sugli assi;
5) Costruisci la bisettrice del 2 e 4 quadrante;
6) Crea il simmetrico di X rispetto alla bisettrice;
7) Traccia la retta passante per -l(su asse y) e per X
8) Traccia la parallela passante per X’(simmetrico di X)
9) Determina il punto di intersezione con l'asse delle x.
Il punto così ottenuto rappresenta _____________, giustifica ciò
con il teorema di Talete: PER LA SOLUZIONE VEDI APPENDICE 2 FIGURA 3
__________________________________________________________________
__________________________________________________________________
2
ATTIVITÁ 2 Costruzione della parabola y= a X
OBIETTIVO:
Ottenere la costruzione della parabola utilizzando il prodotto di due quantità da un punto di vista geometrico
1) Determina un punto appartenente alleasse x che chiami con a
2) Ripeti la procedura dell'attività precedente (punti 7-9) che
deve essere opportunamente modificata per ottenere il prodotto
tra il coefficiente a ed X2
3) Determina il simmetrico di aX2 rispetto al seguente prodotto di
simmetrie: assiale di asse la bisettrice del 2 e 4 quadrante,
centrale di centro O.
Giustifica perché il punto così ottenuto è l'ordinata del punto P
appartenente alla parabola di equazione y =aX2.
__________________________________________________________________
4) Completa la procedura per ottenere il luogo geometrico di P al
variare dell'ascissa X sull'asse.
PER LA SOLUZIONE VEDI APPENDICE 2 FIGURA 4
11
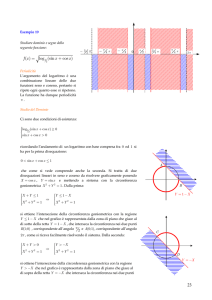
ESEMPIO n°2 LUOGHI GEOMETRICI
Gli alunni sono invitati a compilare le schede proposte durante
l'attività di laboratorio con Cabri. Essi potranno visualizzare,
scoprire o verificare le proprietà delle figura geometrica studiata. La struttura logica. della attività è caratterizzata dalle seguenti fasi:
1.
2.
3.
4.
ANALISI DELL’ENUNCIATO DELLE PROPRIETÁ del luogo;
IL DISEGNO dello stesso con riga e compasso;
LA VERIFICA a computer di quanto esposto su carta;
LA DIMOSTRAZIONE che tutti e soli quei punti godono di quella
proprietà;
5. ESERCIZI non guidati.
Il percorso propone esercizi di difficoltà graduata, invitando
l'allievo ad acquistare un'autonomia crescente.
Ad esempio, nell'attività 1A, l'alunno prende familiarità con le
funzionalità di Cabri e con la struttura logica dell'attività attraverso un esempio semplice. In seguito, attività 2A, per poter
disegnare con questo software il luogo proposto, dovrà riflettere
con attenzione sulle caratteristiche della situazione geometrica.
DESTINATARI:
Alunni del 2 anno di una scuola media superiore.
TEMPO: 3 ore.
PREREQUISITI: Geometria euclidea (fino alla circonferenza).
Il percorso didattico si articola in due parti.
12
A)SCOPRIRE LA FORMA DEL LUOGO CONOSCENDONE LA PROPRIETÁ
DEFINITORIA
Attività 1 Determinazione della forma di un luogo geometrico COME R~DIATA ESECUZIONE
delle istruzioni dell'enunciato
Costruzione teorica e manuale
OBIETTIVO:
Analizzare teoricamente un semplice luogo geometrico
Problema: Determinare il luogo geometrico dei punti medi del raggio di una circonferenza assegnata.
1) Determina un punto M del luogo ed evidenzialo sulla figura.
2) Quale figura descrive il punto M al variare di r: _____________
3) Scrivi una sintetica dimostrazione che giustifichi la risposta
precedente.
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
Costruzione a computer del luogo
OBIETTIVO:
Familiarizzare con l'opzione luogo geometrico e
verificare l'esattezza della costruzione manuale
1) Apri un nuovo foglio
2) Costruisci la circonferenza di centro 0 e raggio r a piacere.
3) Prendi un punto A sulla circonferenza (Costruzione- punto su un
oggetto).
4) Disegna il punto medio di OA (Costruzione - Punto medio).
5) Attiva Costruzione ~ luogo geometrico- e segna come punto del
luogo M e come punto variabile A e trascinalo lungo la circonferenza tenendo premuto il clic del mouse.
13
6) Osserva la figura determinata al variare di A e confrontala con
quella disegnata sul foglio e abbandona il luogo.
7) Esegui ora la verifica con Cabri:
• primo modo tutti i punti del luogo hanno uguale _____________
dal centro(Creazione - segmento OM; Diversi - misura OM.)
• secondo modo disegna la circonferenza centro/punto dal menù
Creazione (centro = O, punto = M) e ripeti quanto al 5 e 6 confrontando le due curve. PER LA SOLUZIONE VEDI APPENDICE 2 FIGURA
5
ESERCIZIO 1: Determina il luogo dei punti che sono vertici dei
triangoli di base assegnate e altezza nota.
ESERCIZIO 2: Determina il luogo dei punti medi delle corde AM di
un angolo convesso PQR con A fisso appartenente a QP e m mobile su
QR
ATTIVITÁ 2 Determinazione della forma del luogo geometrico DOPO UNA TRADUZIONE con
riga e compasso delle istruzioni dell'enunciato
Primo esercizio
Costruzione teorica e manuale
OBIETTIVO:
Individuare il luogo con riga e compasso. Utilizzare alcune costruzioni per realizzare la figura
base del luogo geometrico.
Problema: In un triangolo ABC gli angoli di vertice A (a) e B (b)
sono complementari. Determina il luogo descritto dal terzo vertice
C, con 0°< a < 90°
1) Rifletti: quale tipo di triangolo soddisfa le condizioni del
problema?
__________________________________________________________________
2) Disegna di seguito un qualsiasi triangolo che soddisfi le condizioni precedenti.
3) Rifletti: quali sono gli unici elementi della figura che rimangono invariati al variare di a.
__________________________________________________________________
4) Quale è la forma geometrica del luogo cercato?
__________________________________________________________________
5) Scrivi una sintetica dimostrazione che giustifichi la risposta
precedente.
__________________________________________________________________
14
Costruzione a computer del luogo
OBIETTIVO:
Determinare gli elementi base della costruzione
con Cabri per costruire in maniera corretta il
luogo
1) Apri un nuovo foglio
2) Scrivi in modo cronologico i comandi da utilizzare con Cabri
per la costruzione del luogo richiesto.
Avvio della procedura:
a) disegna un segmento AB
b) retta per.......... PER LA SOLUZIONE VEDI APPENDICE 2 FIGURA 6
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
3) Come puoi verificare l'ipotesi formulata nel punto 4?
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
ESERCIZIO: Determina il luogo del punto medio di una corda uguale
ad un segmento prefissato AB.
PER LA SOLUZIONE VEDI APPENDICE 2 FIGURA 7
15
Secondo esercizio
ATTIVITÁ 3 Costruzione teorica e geometrica dei luogo
OBIETTIVO:
Definire sul foglio la costruzione geometrica
rigorosa di un generico punto del luogo
Problema: Nel Triangolo ABC i vertici A e B sono fissi, mentre C
si può muovere sulla semiretta BC. Determinare il luogo geometrico
descritto dai punti medi delle mediane CM.
1) Disegna di seguito un qualsiasi triangolo che soddisfi le condizioni precedenti.
2) Rifletti: quali sono gli unici elementi della figura che rimangono invariati al variare di C sulla retta r.
__________________________________________________________________
__________________________________________________________________
3) Quale è la forma geometrica del luogo cercato?
__________________________________________________________________
ATTIVITÁ 4 Realizzazione disegno del luogo geometrico
OBIETTIVO:
Disegnare l'intero luogo geometrico con Cabri
1) Apri un foglio;
2) Riproduci su Cabri la figura di cui al punto 1 della attività
precedente:
a) Creazione Retta per due punti
b) Edizione nomi - r c) Costruzione punto su un oggetto (due volte)
d) Edizione nomi - B, C __________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
n) Costruzione Luogo di punti (P al variare di C su r)
PER LA SOLUZIONE VEDI APPENDICE 2 FIGURA 8
16
ATTIVITÁ 5 Verifica con Cabri del luogo
OBIETTIVO:
Controllare mediante l'uso della costruzione predefinita l'esattezza del luogo
1) Nella figura precedente prima di tracciare il luogo disegna
utilizzando Costruzione -___________________- la figura geometrica
(F) luogo di P al variare di C sulla retta r.
2) Ripeti l'opzione Luogo di punti e verifica che P si muove sulla
figura F
ATTIVITÁ 6 Dimostrazioni (varie) della proprietà del luogo geometrico
OBIETTIVO:
Riflettere sui vari modi per dimostrare la proprietà del luogo
Primo modo “misura di segmenti”
1) Il punto P si muove lungo la figura F cioè:
____________________________________ perché la ___________________
di P da r ha una misura
2) Verifica sul foglio di lavoro di Cabri quanto hai affermato al
punto l.
a) Costruzione retta _____________ per P ad r;
b) Costruzione intersezione di due oggetti ___________________;
c) Creazione segmento ___________________;
d) Diversi misura
e) Costruzione luogo di punti
Osserva:
Che cosa si può affermare sulla misura?
__________________________________________________________________
__________________________________________________________________
Secondo modo “dimostrazione sintetica”
1) Sulla figura precedente disegna un nuovo punto C’ su r e traccia il nuovo punto medio P’ di C’M
2) Considera il triangolo CC’A:
la retta PP’ è _____________________ per il teorema ______________
Terzo modo “riga e compasso”
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
Esercizio facoltativo:
Determinare il luogo dei punti del piano che sono gli estremi dei
segmenti MP tangenti in M ad una circonferenza data, con il segmento MP di lunghezza assegnata ed M variabile.
PER LA SOLUZIONE VEDI APPENDICE 2 FIGURA 9
17
B) DISEGNARE CON CABRI UN LUOGO GEOMETRICO NOTO E
DIMOSTRARNE LA PROPRIETÁ DEFINITORIA
ATTIVITÁ 1 Disegno dei luogo proposto con Cabri
OBIETTIVO:
Disegnare la figura base con Cabri
Problema: Disegnare la bisettrice di un angolo assegnato e dimostrarne che si tratta di un luogo geometrico i cui punti godono
della proprietà di essere equidistanti dai lati dell'angolo.
1) Apri foglio;
2) Creazione - punto (tre volte);
3) Edizione - nomi- A, B, C;
4) Creazione - retta per due punti- (A, B);
5) Creazione - retta per due punti- (A, C);
6) Costruzione - bisettrice 7) Costruzione - punto su un oggetto- (bisettrice)
8) Edizione nomi- (M);
9) Diversi angolo - (due volte relativamente a quelli determinati dalla bisettrice);
10) Diversi - misura - (angoli precedenti).
PER LA SOLUZIONE VEDI APPENDICE 2 FIGURA 10
ATTIVITÁ 2 Analisi teorica della proprietà definitoria del luogo
OBIETTIVO:
Dimostrare la proprietà definitoria (tutti e soli)
1) Nella seguente
dell'angolo BAC:
figura
la
semiretta
18
AM
è
la
bisettrice
2) Determina nella figura le distanze di M dai lati AB e AC;
3) Dimostra sinteticamente la congruenza di tali distanze:
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
4) Viceversa: dimostra che se MH = MK, dove H e K sono rispettivamente i piedi delle distanze di M da AB e AC, allora M appartiene
alla bisettrice.
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
ATTIVITÁ 3 Verifica con Cabri del luogo geometrico
OBIETTIVO:
Controllare mediante l'uso della costruzione predefinita l'esattezza del luogo
Riprendere la costruzione precedentemente fatta su Cabri.
1) Costruzione - punto su un oggetto- (retta AB);
2) Edizione - nomi- (punto P);
3) Creazione - circonferenza centro A punto P;
4) Costruzione - intersezione due oggetti - (circonf. e retta AC);
5) Edizione nomi - (punto Q);
6) Creazione circonferenza centro P punto Q- (circonferenza G);
7) Creazione circonferenza centro Q punto P- (circonferenza Gl);
8) Costruzione - intersezione due oggetti- (G e G l);
9) Edizione - nomi- (punti R S);
10) Costruzione - luogo geometrico - del punto R al variare di P.
19
ATTIVITÁ 4 Dimostrazioni (varie) della proprietà del luogo geometrico
OBIETTIVO:
Riflettere sui vari modi per dimostrare la proprietà del luogo
Primo modo “misura di segmenti”
1) Costruire su Cabri i segmenti RH’ e RK’
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
Secondo modo ""dimostrazione sintetica
1) Dimostra che R = (G Ç G l) ha la stessa distanza da AB e AC
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
ESERCIZIO:
Disegnare la bisettrice di un angolo i cui lati r ed s si incontrano fuori dal foglio.
20
APPENDICE 1
OGGETTI – COSTRUZIONI - RELAZIONI
Gli oggetti sono gli elementi indispensabili per la costruzione di
una figura e sono il Punto, la Retta e la Circonferenza.
Le costruzioni si eseguono a partire dagli oggetti fondamentali.
Le relazioni sono quelle che invece vengono a stabilirsi tra gli
oggetti nel corso della costruzione della figura.
ESEMPIO
Per costruire l'asse di un segmento si opera concettualmente in
tre fasi:
1ª si determinano sul foglio i punti A e B(oggetti fondamentali)
che sono gli estremi del segmento;
2ª si esegue la costruzione del segmento che è una costruzione predefinita;
3ª si esegue la costruzione del punto medio e della retta perpendicolare, passante per esso. Si stabilisce una relazione tra segmento e retta: al variare di A e B varia di conseguenza l'asse.
In Cabri vi sono già definite delle costruzioni di base (sono nel
menù CREAZIONE), mentre altre costruzioni definite tra gli oggetti
fondamentali le troviamo nel menù COSTRUZIONE.
Le relazioni tra
gli oggetti invece sono sia nel menù DIVERSI che in quello COSTRUZIONE.
CURSORI
21
DESCRIZIONE DEI CURSORI
1
1. Il cursore con cui si scelgono i menù, con cui si risponde
ai dialoghi, ecc.
2. Il cursore di base, che appare quando non sta succedendo
niente in una finestra di Cabri.
3. Il cursore prende questa forma in prossimità di uno degli
oggetti di base di una figura e indica che è possibile
spostare l'oggetto in questione (il cui tipo è precisato a
fianco del cursore).
4. Questo
cursore
indica
che
è
possibile
selezionare
l'oggetto situato presso la punta della freccia facendo
clic. Il tipo di oggetto è precisato vicino alla freccia.
5. Questo cursore appare quando si può spostare la parte visibile della figura. Lo si vede apparire anche quando si
vuole spostare il nome di un oggetto, la misura di un segmento, ecc..
6. Questo cursore indica che un nuovo oggetto può essere
creato
7. Questo cursore indica che si sta puntando nel rettangolo
che permette di accedere ai messaggi di aiuto.
Cursori specificati nel menù Aspetto degli oggetti:
8. Cursore che serve a rendere gli oggetti invisibili o meglio
trasparenti (finché si resta in questo ambiente gli oggetti
restano tuttavia ancora visibili [in tratteggio] per
consentire di fare "marcia indietro").
9. Cursore che permette di rintracciare in tratto fine un oggetto precedentemente reso invisibile.
10. Cursore che permette di rendere più spesso il tratto oppure di rappresentare un oggetto a colori.
NOTE:
Un cursore a forma di orologio in movimento è utilizzato per avvertire che una operazione in corso può prendere un pò di tempo.
Gli utenti sprovvisti di mouse attivano la barra dei menù grazie
al tasto F10.
TASTI FUNZIONI
•
•
•
•
•
•
•
ALT - A:
ALT - X:
ALT - Z:
ALT - R:
ALT - 0:
ALT - S:
+/- :
ripete l'ultima operazione eseguita.
termina l'esecuzione di Cabri.
annulla l'ultima operazione.
cancella e ritraccia la figura.
apre un file (vedi Archivi)
salva un file
per ingrandire/rimpicciolire una figura,
___________
1
Tutte le definizioni che seguono sono tratte da: Cabri Géomètre
nuale dell'utente -Versione 1.7 per MS-DOS- Loescher Editore Torino
22
–
Ma-
CREAZIONE
• PUNTO: serve per creare un punto nella posizione desiderata
cliccando con il mouse;
• RETTA: serve per creare una retta passante per le due posizioni
iniziale (quella dove viene premuto il mouse) e f inale (quella
dove viene rilasciato il mouse, dopo averlo spostato sul foglio);
• CIRCONFERENZA: serve per creare una circonferenza avente come
centro il punto in cui viene premuto il mouse e come raggio la
lunghezza dello spostamento del mouse finché non viene rilasciato;
• SEGMENTO: serve per creare un segmento: posizionarsi su un punto
e cliccare con il mouse (punto iniziale) e ripetendo la medesima
operazione con un secondo punto (punto finale);
• RETTA PER 2 PUNTI: serve per creare una retta passante per due
punti assegnati;
• TRIANGOLO: serve per costruire un triangolo indicando i tre vertici;
• CIRCONFERENZA (Centro, Punto): serve per disegnare una circonferenza in cui il primo punto assegnato è il centro, mentre il secondo è un punto che sta sulla circonferenza stessa.
COSTRUZIONE
• LUOGO DI PUNTI: serve per creare un luogo geometrico al variare
di un determinato punto.
• PUNTO SU UN OGGETTO: serve per fissare un punto su di un segmento, di una retta o di una circonferenza
• INTERSEZIONE DI DUE OGGETTI: costruisce effettivamente il punto
di intersezione di due oggetti del tipo retta, segmento o circonferenza
• PUNTO MEDIO: serve per selezionare il punto medio di due punti
già assegnati o del segmento che li congiunge.
• ASSE: determina l'asse di un segmento.
• RETTA PARALLELA: serve per disegnare una retta, parallela ad una
assegnata, passante per un punto selezionato (che deve essere
indicato per primo).
• RETTA PERPENDICOLARE: come sopra, solo che viene costruita una
retta perpendicolare a quella assegnata.
• CENTRO DI UNA CIRCONFERENZA: serve per determinare il centro di
una circonferenza selezionata.
• SIMMETRICO DI UN PUNTO: determina il simmetrico di un punto rispetto ad una retta o ad un punto.
• BISETTRICE: serve per costruire la bisettrice di un angolo dopo
aver selezionato i tre punti che definiscono lo stesso angolo
(il secondo punto rappresenta sempre il vertice).
23
EDIZIONE
• ANNULLA: serve per annullare l'ultima operazione.
• CANCELLA TUTTO: serve per cancellare tutti gli oggetti presenti
sul foglio di lavoro
• NOMI: serve per assegnare un nome a punti, rette e circonferenze. Si seleziona un oggetto e si attribuiscono al massimo quattro caratteri all'interno del rettangolo che appare accanto
all'oggetto prescelto.
• PREFERENZE: voce che non deve essere utilizzata.
• ASPETTO DEGLI OGGETTI: serve per cambiare alcuni aspetti delle
figure .
- NERO ROSSO VERDE BLU: servono per colorare la figura prescelta
- MATITA: serve per disegnare con tratto fine la figura e il
cursore si presenta come una matita.
- PENNELLO: serve per disegnare in grassetto la figura prescelta ed il cursore appare sotto forma di un piccolo pennello.
- Il rettangolo:
- GOMMA: serve per rendere "invisibile" una figura ed il cursore appare come una piccola gomma (per tutta la sessione in
cui si usa EDIZIONE l'oggetto appare tratteggiato)
- TUTTO: ridisegna in tratto fine tutte le figure
DIVERSI
• SOPPRIMI UN OGGETTO: serve per eliminare un oggetto che deve essere selezionato(con esso vengono eliminati tutti quelli collegati).
• SOPPRIMI DELLE RELAZIONI: serve a modificare a posteriori le caratteristiche logiche di un oggetto.
• VINCOLA UN PUNTO AD UN OGGETTO: serve per vincolare un punto ad
un oggetto (retta segmento circonferenza) vicino, dopo averli
selezionati.
• MACRO-COSTRUZIONI: serve per fare costruzioni da ripetere automaticamente.
• SCEGLI I MENU': voce che non deve essere utilizzata.
• RICOSTRUZIONE PASSO A PASSO: serve per rivedere la costruzione
fatta passo dopo passo premendo il tasto del mouse.
• SEGNA UN ANGOLO: selezionare tre punti per segnare l'angolo da
essi formato.
• MISURA: selezionare un segmento od un angolo per averne la misura in cm od in gradi. Le misure sono precise al millimetro o al
grado.
24
MACRO COSTRUZIONI
(Costruzione)
E' possibile evitare di rifare una costruzione già eseguita, qualora se ne ripresenti la necessità. Infatti si può memorizzare tale costruzione registrandola sotto un determinato nome per poi poterla caricare ed eseguire ogni volta che occorra.
BARICENTRO
punto di incontro delle mediane
ORTOCENTRO
"
"
"
delle altezze
CIRCOCENTRO
"
"
"
degli assi
l) Apri il file che contiene il triangolo
2) DIVERSI-Macrocostruzioni
3) Box di dialogo clic su NUOVA
4) Clic su FINE DEGLI OGGETTI INIZIALI dopo aver esaurito l'elenco
degli oggetti da cui bisogna iniziare a costruire la macro
(TRIANGOLO).
5) Clic su FINE DEGLI OGGETTI FINALI dopo aver esaurito la serie
degli oggetti finali (ORTOCENTRO, BARICENTRO e CIRCOCENTRO)
6) Immettere il nome per ricordare la macro nel menù COSTRUZIONE
7) Immettere il commento di aiuto
8) Clic su OK e poi dare un nome al file contenente la macro con
estensione .MAC .
MACRO COSTRUZIONI
(Utilizzazione)
1)
2)
3)
4)
5)
6)
ARCHIVI – Nuovo
CREAZIONE – Triangolo
DIVERSI - Macro Costruzioni
Box di dialogo – Apri
Digitare nome del file contenente la macro
COSTRUZIONE e ultima opzione del menù deve essere nome della macro
7) Clic sopra nome macro
8) Selezionare il triangolo e quindi devono apparire i tre punti.
25
FIGURA 1
FIGURA 2
FIGURA 3
FIGURA 4
26
FIGURA 5
FIGURA 6
FIGURA 7
FIGURA 8
27
FIGURA 9
FIGURA 10
28
Con Cabri géomètre
è possibile visualizzare
un luogo geometrico
utilizzando un apposito comando.
Le istruzioni da fornire
richiedono
un’attenta analisi
delle proprietà geometriche
delle figure.
Queste schede di lavoro
guidano alla stesura
delle istruzioni
ed invitano a verificare
le proprietà del luogo
sfruttando le potenzialità
di Cabri
I.R.R.S.A.E. Emilia Romagna - Sezione Scuola Media