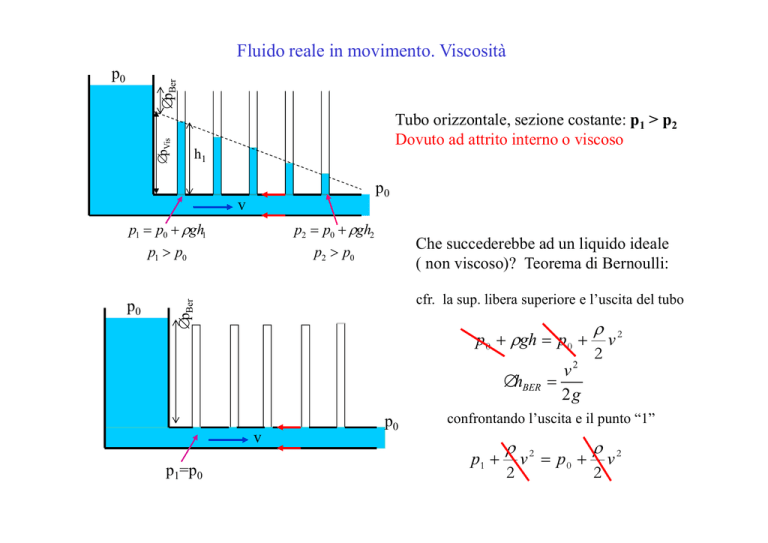
Fluido reale in movimento. Viscosità
∆pBer
p0
∆pVis
Tubo orizzontale, sezione costante: p1 > p2
Dovuto ad attrito interno o viscoso
h1
p0
v
p1 = p0 + ρgh1
p2 = p0 + ρgh2
p1 > p0
p2 > p0
cfr. la sup. libera superiore e l’uscita del tubo
∆pBer
p0
Che succederebbe ad un liquido ideale
( non viscoso)? Teorema di Bernoulli:
p 0 + ρgh = p 0 +
∆hBER =
v
p1=p0
p0
2
ρ
2
v2
v
2g
confrontando l’uscita e il punto “1”
p1 +
ρ
2
v 2 = p0 +
ρ
2
v2
Definizione di viscosità
Sperimentalmente, è necessaria una forza F per mantenere la lamina (di area S) a velocità
costante. Se la lamina è grande (rispetto alla profondità h) si trova:
F = FV ∝ S
lamina di area S
y
FV
v0
F
o meglio
h
v
h
dv
FV = η S
dy
gradiente
di velocità
coefficiente di viscosità o “viscosità”
profilo di velocità
si assume come definzione di viscosità
In un fluido reale in movimento possono esservi forze tangenti alla superficie (di taglio).
Un viscosimetro di uso pratico (2 cilindri coassiali rotanti):
Se la separazione d fra le superfici è piccola (d<<R)
dv
ωR
dF = η dS
= η dS
⇒
dr
d
τ = ηS
ωR 2
fluido
dS
ω
d
Il momento τ che si deve applicare per tenere fermo il cilindro esterno fornisce η
d
Viscosità
[
[η ] =
] [
N
s
−1 −1
−1 −1
⋅
m
⋅
=
kg
⋅
m
s
=
ML
T
2
m
m
nel S.I. kg/ms o Pa.s
]
altre unità:
Poise (P=gcm-1s-1): 1Pa s=10 Poise
η “costante” (non dip. da dv/dy) solo per fluidi “newtoniani”
η può dipendere da dv/dy (ad es. fluidi tissotropici).
s o s ta n z a
A cqua
E ta n o lo
E te re
o lio m o to re
G lic e rin a
a ria
η (2 0 °C ) P a s
1 . 0 1 .1 0 -3
0 . 9 5 .1 0 -3
0 . 1 6 .1 0 -3
0 .8 0
1 .4 8
1 . 8 .1 0 - 5
Dipendenza della viscosità dalla
temperatura nei gas e nei liquidi.
3.5
2
1.8
3
viscosità dell’acqua
-5
η (10 Pas)
1.6
-3
η (10 Pas )
1.4
1.2
1
2.5
2
0.8
1.5
0.6
viscosità dell’aria
0.4
1
0.2
200
0
0
20
40
60
T (°C)
80
100
120
300
400
500
T (K)
600
700
800
Profilo di velocità in un tubo cilindrico con flusso laminare.
Nel flusso laminare si ha stratificazione delle velocità. In generale si può assumere che il
fluido a contatto con la parete abbia velocità nulla.
Per condotti “abbastanza piccoli” con flusso laminare il profilo di velocità ha una
forma paraboloide
Fra gli strati (guaine cilindriche) a diversa velocità agiscono forze viscose. Ad es. lo strato scuro
è rallentato dallo strato adiacente esterno, più lento, e accelerato dallo strato interno più veloce.
Tubo cilindrico in regime laminare. Legge di Poiseuille
Si consideri un condotto orizzontale, di raggio R e lunghezza l
Tubo di flusso di raggio r<R, in condizioni stazionarie
p1S
R
r
r
r
FTOT = FP + FV = 0
p2 S
r
FV
l
Forze di pressione
Forza viscosa
FP = p1 S1 − p 2 S 2 = ( p1 − p 2 )πr 2
FV = η S LAT
dv
dv
=η
2πr l
dr
dr
(il segno è incluso nella derivata)
r
r
FP + FV = 0 ⇒
∆p
dv
=−
r
dr
2η l
con
v( R ) = 0
strato a contatto con la parete
Tubo cilindrico in regime laminare. Legge di Poiseuille
dv
∆p
=−
r
dr
2η l
soluzione:
è un’equazione differenziale,
con la condizione al contorno
1 ∆p 2
(R − r 2 )
v( r ) =
4η l
Quanto vale la portata?
Q =
∫ v ( r ) dS
v( R ) = 0
Profilo di velocità paraboloide
R
=
∫ v (r )2 π
rdr
da cui
0
Legge di Poiseuille
Se si definisce una
«resistenza idraulica»
Q =
π ∆p 4
R
8η l
∆p = R ⋅ Q
quella del tubicino è
8η l
R =
πR 4
Lavoro di una pompa. Liquido ideale
LNC = EMf − EMi
per una massa dm:
P=
lavoro della pompa ed
eventuali forze viscose
dL = dmgh +
dm 2
ρ
v = dV ρgh + v 2
2
2
dL
ρ
= Q ⋅ ρgh + v 2
dt
2
v
∆p ai capi della pompa
∆p = pu − pi = ρgh +
ρ
2
pi = p0 − ρgh1 −
v2
2
v
2
p0
h1
p0
P = ∆p ⋅ Q
ρ
h2
pu = p0 + ρgh2
Potenza dissipata in un condotto.
Per mantenere un flusso costante in un condotto orizzontale si deva applicare
una differenza di pressione
FV
p1S
v
p2S
Le forze viscose compiono lavoro
resistente sull’elemento di fluido,
compensato dal lavoro motore
delle forze di pressione
In un tempo dt, spostamento dx=vdt, il lavoro delle forze di pressione vale:
dL = p1Sdx − p2 Sdx = ( p1 − p2 )Svdt = ∆p ⋅ Qdt
Se il flusso è stazionario l’energia meccanica del fluido nel condotto (cinetica + pot. gravitazionale) non
cambia. Il lavoro delle forze di pressione è opposto a quello delle forze viscose. In modulo, la potenza
dissipata è:
P = ∆p ⋅ Q = R ⋅ Q 2
Il lavoro delle forze di attrito viscoso aumenta l’energia interna del “fluido + condotto”
Potenza dissipata in un condotto. Resistenza idraulica
Si definisce resistenza idraulica di un condotto la grandezza R, definita come
∆p = R ⋅ Q
[R ] = Pa 3⋅ s
m
dove ∆p è la differenza di pressione che mantiene una portata volumica Q.
Per mantenere un flusso costante in un condotto chiuso serve una pompa.
La potenza erogata dalla pompa è:
∆p 2
PV = ∆p ⋅ Q =
= R Q2
R
Condizione per il flusso laminare
La legge di Poiseuille è valida in regime laminare, ma come sappiamo se il flusso è laminare?
Il parametro importante è il
densità del fluido
ρ F vd
R =
η
Numero di Reynolds:
Dimensione caratteristica
(del condotto, del corpo
in movimento ... )
viscosità del fluido
Per un tubo cilindrico assumendo
d=2r
Sperimentalmente, per
un tubo cilindrico lungo:
R =
2 ρ F vr
η
R ≤ 1000
1000 ≤ R ≤ 3000
R ≥ 3000
v: velocità media del fluido,
definita da Q=Sv
regime laminare
regime di transizione
regime turbolento
Convenzionalmente, assumeremo il valore critico (RC=2400) dipende anche da rugosità, lunghezza ...
Nota: il valore critico dipende dalla forma del condotto o, nel caso di moto di un corpo
nel fluido, dalla forma del corpo.
Moto in un fludio reale in moto. Resistenza del mezzo.
Per basse velocità (R <RC)
Per una sfera la forza viscosa vale:
FV = 6πη Rv
R
Legge di Stokes
per forme diverse si può scrivere:
FV = k η l v
Regime laminare
Per alte velocità (R >RC)
dove l è una dimensione caratteristica del corpo
e k un costante numerica dell’ordine delle unità.
Convenzionalmente la resistenza del mezzo si scrive:
scia
FR =
1
cS ρ F v 2
2
densità del fluido
Regime turbolento
Per una sfera ad alta velocità (R >> RC)
Per una sfera in moto in un fluido si può assumere RC=1
c ≅ 0.4 − 0.5
C
Non è così semplice. In realtà C=C(v), o meglio C=C(R)
R
Coefficiente di penetrazione di una sfera in un fluido.
Il valore C~0.5 per una sfera vale per 103 < R <2.105
Valori tipici di c ed S per un’automobile
sono riportati nella tabella a destra:
Moto in un fluido viscoso. Sedimentazione
FV = 6πηRvL
FA = ρF gV
Corpo in caduta in un fluido. FV aumenta con la velocità:
esiste una velocità limite (o di sedimentazione)
F
mg − F A = ( ρ − ρ F )gV
Ad una certa velocità la
forza totale è nulla e la
velocità diviene costante.
mg= ρgV
FV
vL
v
La condizione di velocità limite,
per una sfera in regime laminare:
L’andamento lineare di FV
in figura vale per piccole
velocità (regime laminare)
6πη Rv L + ρ F gV − ρgV = 0
vL
2
2 ( ρ − ρ F ) gR
vL =
9
η
v
t
velocità in funzione del tempo
Moto in un fluido viscoso. Sedimentazione
La velocità di sedimentazione dipende dalla densità, dimensioni e forma.del corpo.
Ciò permette di separare corpi in sospensione di densità, dimensioni o forme diverse.
Per corpi di piccole dimensioni i tempi possono essere molto lunghi.
Esempio.
Sferetta di raggio 5,0µm, densità 1.02 g/cm3, in acqua (1.0g/cm3, η=0.0010 Pas).
La velocità di sedimentazione è 1.1.10-6 m/s. Il tempo di decantazione con h=10cm è ~ 25.5 h
Per ridurre i tempi di sedimentazione si ricorre alla centrifugazione.
ω
In tal caso:
dmF ω2r
dm ω2r
con
2 (ρ − ρ F ) g ′ R 2
vL =
9
η
g′ ≅ ω 2 d
(purché ω2d >> g)
d
Se d=10 cm, basta f=5Hz per avere g’~10g. Ultracentrifughe 103 Hz.
Se f=100Hz (12000 rotaz/minuto): vL=0.0044 m/s.
La sedimentazione su una distanza di 10cm avviene in circa 23 s
Velocità limite di una goccia di pioggia.
r (µ m)
1
2
10
20
100
Secondo la legge di Stokes (R<1)
vL
(
ρ − ρF )gV 2 ρ gr2
=
≅
kη l
9 η
v (m/s)
1,2E-04
4,8E-04
1,2E-02
4,8E-02
1,2E+00
Re
1,6E-05
1,3E-04
1,6E-02
1,3E-01
1,6E+01
R>0.2
Per gocce grandi non vale la legge di Stokes
12
Velocità limite delle gocce di pioggia.
Dati per 10<R<1000.
A questi diametri le
gocce si deformano
10
la curva riflette il fatto che C=C(v)
nell’intervallo considerato.
v (m/s)
8
6
4
2
0
0
0.2
0.4
0.6
r (mm)
0.8
1
1.2
Immagini di una tempesta di sabbia vista da statellite.
circa 1012 kg l’anno dal Sahara
... e non solo polvere!
Andamento epidemico della Sindrome di Kawasaki
X. Rodò et al. Scientific Reports 1, 2011
Similitudine meccanica
A causa della complessità del moto dei fluidi le prove con modelli (ad es. in galleria
del vento) sono spesso ancora l’unico modo per studiare le forze agenti su una struttura
(Ad es. automobili, aerei, ma anche edifici, ponti ....)
Come si scalano le forze misurate sul modello alla struttura reale?
F =
1
c (R )S ρ v 2
2
Fm =
1
2
c m (R )S m ρ m v m
2
Poiché il coefficiente C dipende da R in modo complesso, la condizione più
importante è che le prove su modello si facciano con lo stesso numero di Reynolds.
ρ vd ρ m vm d m
R=
=
η
ηm
Similitudine meccanica
Condizione per la riproducibilità (in scala) delle forze agenti su un corpo in moto in un
fluido è che abbia lo stesso numero di Reynolds.
Simulazione del volo degli insetti
(Le Scienze 394, 2001, p.64)
“ala” del simulatore
ala di moscerino in aria
d ≅ 25 cm
d ≅ 2 . 5 mm
f ≅ 200 Hz
ρ vd ρ f d 2 costante
R=
∝
η
η
in olio
f ≅ 0.2 Hz
ηOlio
ηAria
⇒
= 10
ρOlio
ρ Aria
Per un essere molto piccolo è come se il mezzo fosse molto più viscoso (rapportato alle
nostre dimensioni).
2
ρ
ρ
v
d
d
Se v ∝ d ⇒
R=
∝
υ = η ρ viscosità cinematica.
η
η
d ≅ 1.0m v = 102 m/s ρ = 1.2kg/m3 η = 1.85 ⋅10−5 Pas ⇒ R ≈ 107
aereo
d ≅ 10−3 m v = 10 m/s ρ = 1.2kg/m3 η = 1.85 ⋅10−5 Pas ⇒ R ≈ 103
insetto
Regimi molto diversi. Le forze non si possono scalare.
Moto in fluidi reali. Un caso molto complesso.
Il volo della “testa di morto”. (Nature, 1996)
Il volo di un insetto non si può comprendere senza
considerare il moto vorticoso, che è estremamente
difficile da trattare. Gli esempi citati mostrano che
il problema è attuale.
t/T=0.25
t/T=0.44
t/T=0.74
t/T=0.99
Calabrone sospeso a mezz’aria (Physical Review Letters, 2000). Un calcolo 2D.