Fluidi II
Applicazioni della legge di Bernoulli
Viscosità
Legge di Poiseuille
Fluidi in regime stazionario
Tensione superficiale
Capillarità
Applicazioni della legge di Bernoulli
Dilatazione (aneurisma) e restringimento (stenosi) di un
vaso sanguigno sono le patologie vascolari più comuni.
Aneurisma
Teorema di Bernoulli per un condotto orizzontale:
p1+½ ρ v12=p2+½ ρ v22
p1 - p2 = ½ ρ (v22 – v12)
S1v1=v2S2
da cui v1 = v2 S2 / S1
p1 - p2 = ½ ρ v22(1 - S22/S12)
Nel caso di dilatazione S2>S1 da cui p1 - p2 < 0 (p2>p1)
à Vi è una tendenza a incrementare la
dilatazione!!!
Aneurisma
Video su possibile terapia: h1ps://www.youtube.com/watch?v=FfuHNG3mHJY Stenosi
Teorema di Bernoulli per un condotto orizzontale:
p1+½ ρ v12=p2+½ ρ v22
p1 - p2 = ½ ρ (v22 – v12)
S1v1=v2S2
da cui v1 = v2 S2 / S1
p1 - p2 = ½ ρ v22(1 - S22/S12)
Nel caso di restringimento S2<S1, p1 - p2 > 0 (p2>p1)
à Vi è una tendenza ad un’ulteriore
restringimento!!!
Stenosi
Fluidi reali: moto viscoso
Per un fluido ideale la pressione è la stessa in entrata e in uscita.
Questo perché non c’è attrito interno fra le molecole del fluido, né attrito fra
il fluido e le pareti del condotto in cui il fluido scorre. Dunque, in caso di un
condotto a sezione costante e orizzontale, avremo:
p + ρ g h+ ½ ρ v2 = k p + ½ ρ v2 = k’
e dato che la velocità di ogni strato di fluido é la stessa:
p = k’’
ovvero la pressione è costante.
Fluidi reali: moto viscoso
Per i fluidi reali la pressione diminuisce nel verso del moto a causa
dell’attrito interno, o viscosità. Questa in genere è debole nei gas ma
rilevante nei liquidi.
Il condotto esercita una forza resistente sul fluido a contatto (forze di
contatto o adesione solido-liquido), a loro volta gli strati di fluido esercitano
delle forze di attrito che si oppongono allo scorrimento (forze intermolecolari
di coesione). La velocità è massima al centro e nulla sul bordo.
v = v(r) ∝ ( R 2 − r 2 )
parabola Fluidi reali: moto viscoso
In un fluido reale il Teorema di Bernoulli deve tener conto
dell’energia persa per attrito:
p1+½ ρ v12 + ρ g h1 = p2+½ ρ v22 + ρ g h2 + Eattrito
Nel caso h1=h2, v1=v2 si ha quindi: ΔP=Ea&rito à occorre una differenza di pressione per far muovere un fluido a velocità costante in un condo&o re:lineo ove vi siano degli a&ri< Fluidi reali: moto viscoso
Coefficiente di viscosità
Consideriamo un fluido suddiviso in strati infinitesimi
paralleli tra loro, di area A e a distanza Δx l’uno
dall’altro che scorrono l'uno sull'altro, ciascuno con
velocità caratteristiche (moto laminare).
La forza di attrito viscoso fra uno strato e l’altro è
data dalla relazione:
F = η A Δv/Δx
• Δv/Δx gradiente di velocità
• η coefficiente di viscosità; nel SI si misura
in Pa·s; nel CGS in barie·s = Poise (P).
• 1 Pa·s = 10 P
Dipendenza dalla temperatura
Il coefficiente di viscosità η dipende dalla natura del
liquido. Per uno stesso liquido dipende in maniera molto
marcata dalla temperatura: al crescere di questa diminuisce
molto rapidamente (esempio dell’olio in una padella).
Liquido
Temperatura (°C)
η (Pa·s)
Acqua
0
20
37
100
1.8·10-3
1.0·10-3
6.9·10-4
2.8·10-4
Mercurio
20
1.5·10-3
Sangue intero
37
4.0·10-3
Plasma sanguigno
37
1.5·10-3
Legge di Poiseuille
Abbiamo visto che per fluidi reali
l’esperienza mostra che la
pressione diminuisce nel verso del
moto a causa della viscosità.
Per mantenere un liquido in moto in un condotto è
necessaria quindi una differenza di pressione Δp fra
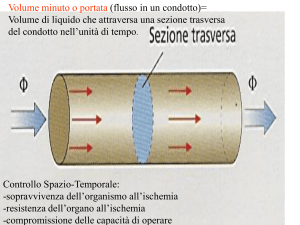
l’ingresso e l’uscita. La portata Q attraverso il condotto
dipende da Δp oltre che dalla lunghezza, dalla sezione del
condotto e dalla viscosità η.
Se il condotto è un cilindro orizzontale di raggio R e
lunghezza L, la portata Q è espressa da:
Q = (π Δp R4)/(8ηL) legge di Poiseuille
(usata nei viscosimetri)
Regime laminare e turbolento
Finora abbiamo considerato un fluido suddiviso in strati
paralleli tra loro che scorrono l'uno sull'altro, ciascuno
con una certa velocità (moto laminare). Se invece ci
sono dei vortici che portano a un rimescolamento del
fluido con distribuzioni irregolari e continuamente
variabili di velocità, il moto è turbolento.
Numero di Reynolds
Per stabilire se il moto di un fluido viscoso è laminare
o turbolento si definisce una grandezza adimensionale
chiamata numero di Reynolds: NR= ρ v l / η.
Questo parametro dipende dalla velocità media v del
fluido (rispetto al solido con cui viene a contatto),
dalla densità ρ, dalla viscosità η, e da una grandezza
lineare l caratteristica del condotto (per una forma
cilindrica, ad esempio, l coincide col diametro).
Si dimostra sperimentalmente che, per tubature
rettilinee di sezione circolare, il flusso della corrente
fluida è laminare per valori di NR inferiori a 1000, e
turbolento per valori superiori a 3000.
Regime laminare e turbolento
Regime laminare e turbolento
Il sistema circolatorio
Una delle funzioni del sistema circolatorio è quella di
trasportare ossigeno dai polmoni ai tessuti e di trasportare
in senso inverso l’anidride carbonica prodotta dalla
respirazione cellulare. Ciò si realizza mediante un circuito
chiuso che costringe il sangue a passare successivamente
attraverso i polmoni e tutti gli altri tessuti.
Il cuore
Per spingere il sangue attraverso i capillari polmonari
e quelli tissutali è necessaria una pompa, il cuore, da
cui si dipartono piccola e grande circolazione.
Parti attive sono ventricoli, che contraendosi
spingono il sangue.
Piccolo e grande
circolo
Il circolo polmonare (o
piccolo circolo) origina
dal ventricolo destro con
l’arteria polmonare e
termina nell’atrio sinistro
con la vena polmonare.
Il grande circolo (o
circolo sistemico) parte
dal ventricolo sinistro
con l’aorta ed entra
nell’atrio destro
mediante la vena cava.
Piccolo e grande
circolo
Il cuore si può
considerare come
l’insieme di due pompe
che lavorano in serie su
tratti diversi del circuito,
sebbene siano unite a
formare un unico
organo.
Le contrazioni e
successive dilatazioni dei
ventricoli sono dette
sistole e diastole
rispettivamente.
Piccolo e grande circolo
Piccolo circolo Poiché il circuito sistemico è
molto più esteso di quello
polmonare (e quindi offre
maggiore resistenza), il
ventricolo sinistro deve
produrre una differenza
maggiore rispetto al destro.
Non a caso la muscolatura
del VS è maggiore di quella
del VD, che lavora di meno.
Diramazione dei condotti
Ciascuna delle due circolazioni inizia con vasi di grosso calibro
(arterie) che si suddividono in rami più piccoli (arteriole)
Le arteriole a loro volta si
sfioccano in numerosi
capillari, attraverso le cui
pareti avvengono i processi di
scambio con i tessuti
circostanti.
Successivamente il processo di
ramificazione si inverte: i
capillari confluiscono in vasi di
maggiori dimensioni (venule)
e si raccolgono in vasi sempre
più grandi (vene) che
riportano il sangue al cuore.
Il sangue come fluido
Il sangue è un liquido viscoso che, in generale, scorre
nel sistema circolatorio con moto laminare. Il moto
turbolento, essendo rumoroso, può essere rilevato
mediante auscultazione con un fonendoscopio.
Il passaggio da moto laminare
a moto turbolento nel sangue
sta alla base del principio di
funzionamento dello strumento
usato per misurare la pressione
arteriosa (sfigmomanometro).
Misura della pressione arteriosa
Immettendo l’aria nel manicotto si comprime l’arteria
brachiale. Ad una riduzione di sezione corrisponde un aumento
della velocità del sangue: si passa da moto laminare a
turbolento, rivelabile con il fonendoscopio.
Misura della pressione arteriosa
Aumentando la pressione il rumore scompare. Questo perché la
arteria si è chiusa, e tale chiusura avviene ad una pressione del
manicotto che deve essere poco superiore a quella massima
nell’arteria.
Si lascia allora diminuire la
pressione facendo sfiatare l’aria.
La P a cui riprende la circolazione
e ricompare il rumore, è la
pressione massima arteriosa
(sistolica).
La P a cui scompare
successivamente il rumore, perché
il sangue è tornato al moto
laminare, si assume come
pressione minima arteriosa
(diastolica).
Lo sfigmomanometro
Tensione superficiale
Nella materia allo stato liquido ogni molecola è circondata da altre
molecole: le forze attrattive tra molecole, poiché ognuna di esse è
completamente circondata da altre, si bilanciano permettendo che
ognuna si sposti liberamente (non vi è prevalenza di forze in una
qualche direzione).
Consideriamo, appena sotto la
superficie, uno strato spesso
quanto il diametro delle
molecole; questo strato (detto
strato limite) è quello in cui
avviene il passaggio dallo stato
liquido a quello di gas.
Una molecola che si trovi in
questa zona non ne ha altre
dello stesso tipo al di sopra.
Tensione superficiale
Se una molecola che si trova nello strato limite viene sollevata, i
legami tra essa e le molecole adiacenti vengono tesi, generando
una forza che tende a richiamarla verso la superficie, proprio
come una membrana tesa.
Allo stesso modo, un corpo
minuscolo (pond skaters,
insetti pattinatori) che si
appoggi sulla superficie di un
liquido in modo da non
perforarla, fa si che le
molecole superficiali del
liquido vengono spinte verso
il basso generando una forza
di richiamo diretta verso
l'alto.
Oltre agli insetti c’è il caso
curioso di un rettile, il
basilisco. Coefficiente di tensione superficiale
La tensione superficiale di un liquido rappresenta il lavoro
richiesto per aumentarne la superficie libera. Si dimostra che tale
lavoro può essere espresso in termini della forza di contrazione
esercitata su una linea ipotetica di lunghezza L posta sulla
superficie (forza per unità di superficie):
τ = F/2L
(dove il fattore 2 deriva dal fatto
che i lati della linea sono due)
Il lavoro fatto per “aprire” una
superficie di area S sara’ dunque:
L=τS
Nel SI τ si misura in N/m o J/m2
Liquido
Temperatura (°C)
Tensione
superficiale (N/m)
Acqua
0
20
50
100
0.076
0.073
0.068
0.059
Olio d’oliva
18
0.032
Mercurio
20
0.436
Sangue intero
37
0.058
Plasma sanguigno
37
0.073
In generale τ diminuisce al crescere della temperatura: nei
liquidi più caldi, infatti, è indebolita dal moto di agitazione
termica delle molecole.
L'acqua calda ha quindi migliori proprietà detergenti giacché
la sua minor tensione superficiale permette di raggiungere
più facilmente porosità e fessure.
Per ridurla ulteriormente si fa uso di tensioattivi (come i
detersivi) che si frammentano più facilmente e si disperdono
con maggiore facilità sul materiale che si vuole pulire.
Capillarità
Tubi di sezione molto piccola (diametro
di qualche decimo di mm) sono detti tubi
capillari, in cui la superficie si dispone
secondo una sezione concava o convessa.
Il fenomeno, detto capillarità, si spiega
col fatto che in un liquido esistono delle
forze di coesione, di natura elettrica e
attrattive, fra molecole simili. Invece, la forza tra la molecola di un
liquido e un'altra sostanza (es. vetro della parete di un recipiente
che contenga il liquido) è detta forza di adesione.
Si dice che un liquido bagna la superficie di un'altra sostanza
quando le forze di adesione prevalgono su quelle di coesione
(acqua): in questo caso, si ha risalita del fluido lungo un tubo
capillare e la sua superficie è concava verso l'alto.
Viceversa, quando dominano le forze di coesione (mercurio) il livello
del fluido tende a decrescere e la sua superficie è convessa.
Bolle di sapone e embolia
Si dimostra che una bolla di sapone (o altro materiale/interfaccia)
sferica di raggio R e coefficiente di tensione superficiale τ è in
equilibrio se la tensione superficiale è tale da contrastare la Δp tra
interno ed esterno, per cui vale la relazione:
Δp=2τ/R
Bolle di sapone e embolia
Quando si crea un embolo in un vaso sanguigno, il menisco che
viene spinto dal flusso ha un raggio di curvatura maggiore di
quello che si trova a valle, e quindi
Δp2>Δp1 Δp2-Δp1 > 0
R1 R2 Il verso di questa pressione
è rivolto in senso opposto
al flusso sanguigno.
Flusso sanguigno Se abbastanza grande, la differenza può equilibrare la pressione
del sangue e provocare arresto circolatorio.
Per questo motivo bisogna sempre fare uscire l’aria dalle
siringhe prima di iniettare un qualunque fluido all’interno
del corpo!!!