Fluidodinamica
Liquido perfetto o ideale:
• Incomprimibile (densità costante sia
nel tempo che nello spazio) • Assenza di attrito interno
(in un liquido reale si conserva la caratteristica dell’incompressibilità ma le molecole non sono libere
si dice che il liquido presenta viscosità)
di scorrere le une sulle altre, incontrano resistenza,
Equazione di continuità
Incompressibilità Q=V/Δt=costante La portata Q resta costante: il volume di liquido che entra nell’intervallo di
tempo Δt da un estremo di un condotto è uguale a quello che esce dall’altro
estremo nello stesso intervallo di tempo.
Q=V/Δt=Sh/Δt=Sv(velocità) (m3/s)
v
S
h
s⊥v
h
1
S * v = costante S e v sono inversamente proporzionali ne segue che aumentando la sezione del
condotto diminuisce la velocità e viceversa: se S si dimezza v raddoppia
Alcune Premesse:
Linea di flusso: sempre tangente al vettore velocita` di una particella elementare di fluido.
Queste linee rappresentano le traiettorie di ogni singola particella.
P2
P3
P4
P5
P1
Flusso Laminare
Le linee di flusso non si intersecano
(per un punto passa una sola linea) 2
Flusso
Turbolento
Teorema di Bernoulli: principio di conservazione dell’energia nel caso di un liquido
perfetto
• fluido incompressibile
• non viscoso
• flusso laminare
• flusso stazionario (v(x,y,z,t) non dipende dal tempo)
Le prime due proprietà caratterizzano un liquido ideale. 3
1
S1dx1 = S2 dx2 = ΔV
S1
dx1
2
z1
S2
v1
z2
dx2
v2
p1S1
dopo
prima
p2S2
Lp = P1 ΔV − P2 ΔV
Lg = mgz1 − mgz2
4
Per il teorema dell’energia cinetica si ha dunque:
1
1
2
P1 ΔV − P2 ΔV + mgz1 − mgz2 =
mv2 − mv12
2
2
Da cui si ottiene l’espressione nota come Teorema di Bernoulli :
P1 ΔV − P2 ΔV + ρΔVgz1 − ρΔVgz2 =
1
1
ρΔVv 22 − ρΔVv12
2
2
1
1
2
P1 +
ρv1 + ρgz1 = P2 +
ρv22 + ρ gz2
2
2
Che più semplicemente si può scrivere come:
1 2
P + ρv + ρgz = costante
2
Conservazione dell’energia per unità di volume
5
€
Alcune applicazioni
Tubo di Venturi.
S1
la portata è costante la velocità è maggiore e la pressione
minore dove la sezione è minore
S2
v2
v1
P1
h
P2
Q = S1 v1 = S2 v2
Q
2
ρ 2
z1 = z2 ⇒ Δp = (v2 − v12 )
2
⇒
2
2
2 Δp %
S
S
(
1
2
'
*
=
2
2
ρ & S1 − S2 )
2
%
(
1
S
2
ΔP = P1 − P2 = ρv1 ' 1 2 −1*
2
& S2
)
Flussimetro per la misura della velocità del sangue in un’arteria
6
Tubo di Pitot
Tubo di P. inserito in un flusso di corrente permette di
misurare direttamente la velocità del flusso, x
In b si interrompe la linea di flusso Vb=0 punto di ristagno , in
a la velocità rimane con buona approssimazione quella del
flusso. Dall’equazione di Bernoulli. 1
Pb − Pa = ρ v 2
2
dove ρ è la densità del fluido.
Pa + ρ m hg + ρ gx = Pb + ρ g ( x + h )
Pb − Pa = ( ρ m − ρ ) gh
1
Pb − Pa = ρ v 2 = ( ρ m − ρ ) gh
2
dove ρm è la densità del fluido manometrico.
7
h
L. Torricelli
v
v=
B
2 gh
Sifone
h2
P = P0 − ρg( h1 + h2 + h3 )
h1
A
h3
€
C
v 2 = 2g (h1 + h3 )
8
Esempi
• Il flusso sanguigno in una grande arteria di un cane è incanalato in un flussimetro di
Venturi. La parte più larga ha un’area A1=0.08cm2 uguale alla sezione dell’arteria, la
parte più stretta A2=0.04cm2 in questi due punti si misura una ΔP=25Pa. Qual’è la
velocità del sangue nell’arteria? (densità del sangue ρs=1059kg/m3)
• Un cilindro in cui viene fatto il vuoto ha la base di raggio R=0.5m . Calcolare la
forza che agisce sulla base a) in aria a livello del mare, b) in acqua alla profondità
h=10.33m
• Un corpo di densità ρc=0.9g/cm3 è parzialmente immerso in acqua (ρL=1g/cm3).
Quale frazione del volume totale emerge dall’acqua?
• Una mongolfiera piena di gas (ρg=0.2kg/m3) è in equilibrio in aria (ρa=1.3kg/m3)
sostenendo un carico totale M=300kg. Qual’è la massa del gas nell’ipotesi che il
volume del carico sia trascurabile rispetto al volume del gas
9
Paradosso idrodinamico
Tra due dischi A e B fluisce
dell’aria trasportata dal
condotto O
A
B
O’
O
1
p + ρv 2 = costante
2
€
Attraverso il tubo OO’ arriva una corrente fluida tra i due dischi A e B. Tuttavia il piatto B non viene
respinto ma attratto verso A. L’aumento di velocita` che crea la strozzatura va a scapito di una
diminuzione di pressione che se scende al di sotto di quella atmosferica il disco B tendera` a chiudere il
il tubo anziche` volare via. 10
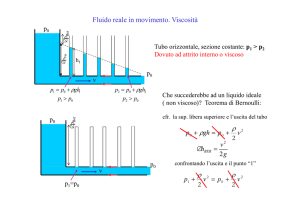
Flusso dei fluidi viscosi
• I liquidi reali presentano dell’attrito interno: vi è dissipazione di energia
meccanica in calore⇒ΔI≠0; Liquido ideale v
Liquido reale P1
v
P2
gli attriti interni sono responsabili della caduta di pressione lungo il condotto
(P2< P1) fenomeno noto come perdita di carico
Potenza dissipata: ΔP* Q=ΔP*S*v
11
fluido in equilibrio: le forze di superficie si riducono alla sola
pressione p=dFn/dS
fluido in movimento: devono essere considerate anche le forze di
coesione tra elementi di fluido (forze intermolecolari attrattive). Il parametro che quantifica l’attrito interno è la viscosità
Flusso laminare
y
A
vO
F
Lo strato di fluido a contatto con la lastra
in movimento ha la stessa velocità della
lastra v; lo strato prossimo alla base fissa
è in quiete v=0
Applicando una forza F alla tavola (di
superficie S) la sua velocità, a regime è
costante: equilibrio tra F applicata ed una
forza di attrito A
Δv
F = ηS
Δy
η Coefficiente di viscosità
12
[η ] = "# ML−1T −1 $%
dimensioni del parametro viscosità
" N
s$
unità di misura ' 2 ⋅ m ⋅ ( = "
kg ⋅ m −1s −1 $
= Pa ⋅ s
#
%
#m
m%
1 Pas = 10 Poise (g cm-1s-1)
13
Flusso laminare in un condotto cilindrico
Q=S<v>=Svmax/2
La portata dipende dalla viscosità del fluido, dalla caduta di
pressione, dal raggio e dalla lunghezza del tubo Legge di Poiseuille
Q=
• basse velocità (regime laminare:
strati scorrono uno sull’altro)
• condotto rigido • piccoli diametri
πΔP 4
ΔP
r =
8ηl
R
ΔP ⋅ r 2
< v >=
8ηl
€
€
14
Ricaviamo la legge di Poiseuille
forza viscosa F = ηS
dv
dy
-Condotto cilindrico in cui il fluido si muove come indicato
delle frecce.
-In regime laminare il moto è schematizzabile come il
moto di tanti cilindri concentrici di velocita` decrescente
man mano che ci avviciniamo alle pareti del condotto
-La forza che contrasta l’attrito viscoso è dovuta alla ΔP €
ΔP ⋅ π r 2 = η 2 π rl
dv
dr
vmax
ΔP ⋅ R 2
< v >=
=
2
8ηl
dv ΔP ⋅ r
=
dr
2ηl
R
vmax − 0 =
∫
0
ΔP ⋅ r
ΔP ⋅ r
dr =
2ηl
4ηl
2 R
2
4
ΔP
⋅
R
ΔP
⋅
π
R
Q = Av = π R 2
=
8ηl
8ηl
0
15
Condizione per il moto laminare
Il tipo di flusso (il genere di moto in un fluido) dipende dal
Re
Numero di Reynolds
=
ρvd
η
dens. fluido
€
Adimensionale
dimensione caratteristica (del condotto, del corpo in
movimento)
Per un condotto cilindrico d=2r. Assumeremo d=2r : Tubo cililndrico: Re =
2 ρvr
η
v: velocità media
del fluido (Q=Sv)
Con questa definizione si trova, per un tubo cilindrico lungo(l>>r):
€
$Re ≤ 1000
regime laminare
&
transizione
%1000 ≤ Re ≤ 3000
&Re ≥ 3000
turbolento
'
€
Tipicamente si assume 2400 come valore critico (ReC): dipende dalla rugosità della superficie e
dalla lunghezza del tubo. ReC =
2 ρ vC r
η
vC: velocità critica. 16
€
Resistenza che incontra un corpo che si muove in un fluido con basse velocità
(Legge di Stokes)
A = 6πηrv
Per un corpo sferico di raggio r
r
solo regime laminare
• Moto (esponenzialmente) smorzato.
• Velocità limite (pioggia, pulviscolo) In generale
A =
A = γv K
1
cSρv 2
2
con 1 < K < 2
Attrito viscoso su sfera ad alta velocità. Regime turbolento
c : coefficiente di aerodinamicità,
S:sezione del corpo perpendicolare al moto del fluido
17