Fluidodinamica
In generale la descrizione del movimento di un fluido è molto
complicata: considereremo per semplicità moti STAZIONARI.
Tutte le particelle di fluido si muovono nella medesima direzione
parallelamente all’asse del condotto e la velocita` del fluido in un dato
punto è sempre la stessa nel tempo.
1
Regime laminare e Turbolento
lamine e profilo
parabolico di velocità
velocità critica
v > vc
Vc≈2000η/2ρr
lamine spezzate
e vortici
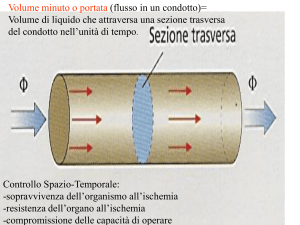
La grandezza che descrive il moto del fluido è la PORTATA:
l
V
Q = Δt
V
Δt
Per un condotto rigido cilindrico V = S l
Q = S l/Δt = S v
rapporto tra il volume di
fluido che, nell’intervallo di
tempo Δt, attraversa una
superficie S del condotto (⊥
alla velocita` ) e l’intervallo
Δt stesso.
3
Equazione di continuità
Incompressibilità
Q=V/Δt=Sv=costante
Portata massica Qm=ρV/Δt=ρSv=costante
Portata volumetrica
Se non esistono ‘perdite’ o
sorgenti lungo il condotto,
la portata Q resta costante.
S1
S1
v1 S1= v2 S2
v1 = v2
S2
S2
Se S2 > S1
v2 < v1
Nel S.I. la portata volumetrica Q si misura in m3 s–1
la portata massica Qm si misura in kg s–1
4
EQUAZIONE di CONTINUITA'
S1 v1 = S2 v2
A
C
B
S = 0.5 cm2
Q=100 cm3s-1
S = 5 cm2
S = 5 cm2
v = 20 cm s–1
S = 1.25 cm2
S = 1.25 cm2
v = 80 cm s–1
S = 2.5 cm2
v = 40 cm s–1
Fluidi ideali
In molte circostanze si può considerare il liquido come ‘ideale’ ossia a densita` costante e
non viscoso (si possono trascurare gli attriti con le pareti e tra le molecole stesse).
Applicando il PRINCIPIO DI CONSERVAZIONE DELL’ENERGIA ad un elemento di
fluido di volume unitario:
p2
p1
h2
h1
Lavoro delle forze di pressione + energia cinetica + energia potenziale = COSTANTE
6
Teorema di Bernoulli: principio di conservazione dell’energia nel caso di un
liquido perfetto
• fluido incompressibile
• non viscoso
• flusso laminare
• flusso stazionario (v(x,y,z,t) non dipende dal tempo)
7
1
2
dx1 S
1
z1
dx2
v1
z2
v2
S2
p1S1
prima
dopo
p2S2
Lp = P1 !V " P2 !V
Lg = mgz1 " mgz2
8
Per il teorema dell’energia cinetica si ha dunque:
1
1
2
P1 !V " P2 !V + mgz1 " mgz2 = mv2 " mv12
2
2
Da cui si ottiene l’espressione nota come Teorema di Bernoulli :
P1 !V " P2 !V + #!Vgz1 " #!Vgz2 =
1
1
#!Vv 22 " #!Vv12
2
2
1
1
2
P1 + !v1 + !gz1 = P2 + !v22 + ! gz2
2
2
Che più semplicemente si può scrivere come:
1
P + !v 2 + !gz = costan te
2
Conservazione dell’energia per unità di volume
9
L = F x = p S x = p ΔV
L/ΔV = p
NB! ΔV unitario!
Ec = m v2/2 = ρΔV v2 /2
Ec/ΔV = ρv2 /2
E p = m g h = ρΔV g h
Ep/ΔV = ρg h
dunque:
p +
ρ v2
/2 +
ρ
g h = COST
è nota come legge di Bernoulli.
10
Esempio n. 1:
STENOSI E ANEURISMA
Se S2 = 0.5 S1
v2 = 2 v1
v22= 4 v12
p1 + ρ v12/2 = p2 + ρ v22/2
p2 = p1 - 3 ρ v12/2
la pressione nella stenosi diminuisce!
S1
S2
Viceversa nel caso di un aneurisma
la pressione aumenta!
11
Es. n. 2 : inserzione di cateteri
Direzione del flusso
Misura la pressione
idrostatica p
Misura la pressione
‘cinetica’ p - ρv2/2
Misura la pressione
‘cinetica’ p + ρ v2/2
12
Diamo i numeri…..
In un individuo a riposo la velocità media del sangue attraverso
l’aorta è pari a 0.33 m/s. Qual è la portata sanguigna, se
il raggio dell’aorta è di 9 mm? (5 l/min)
13
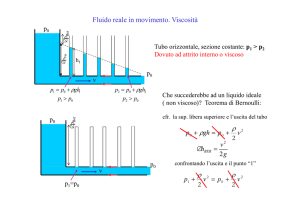
Viscosita`
Nei fluidi reali sono presenti forze di attrito interno che ne ostacolano il moto
I vari strati di fluido incontrano un certo attrito scorrendo gli uni sugli altri
Liquido reale
Liquido ideale
v
P1
v
P2
gli attriti interni sono responsabili della caduta di pressione lungo il condotto (P2< P1)
fenomeno noto come perdita di carico
Potenza dissipata: ΔP* Q=ΔP*S*v
14
REGIME LAMINARE
FORZE di ATTRITO
→
FA
→
=–ηA v
δ
A
→
v2
δ
→
v1
→
→
v
–
v
v = velocità relativa = 1 2
η coefficiente di viscosità
→
[M][L][t]–2 [L]
–1[t]–1
=
[M][L]
[η] =
[L]2 [L][t]–1
S.I. η si misura in Pa s
A
REGIME LAMINARE
Viscosita` η funzione della temperatura
η (poise= gr s-1cm-1)
t (°C)
H2O ........... 0°C ........ 0.0178
10°C ........ 0.0130
20°C ........ 0.0100 ≈ plasma
alcool ........ 20°C ........ 0.0125
etere ..........20°C ........ 0.0023
mercurio .. 20°C ........ 0.0157
glicerina ... 15°C ........ 2.340
aria ........... 15°C ........ 0.00018
sangue ........................... 0.0400
1 poise=10-1 Pa s= 10-1kgs-1 m-1
Fluidi Reali in Regime Laminare
1
formula di Poiseuille
π r4
Q=
8ηl
2
p1
p1 > p2
(p1 – p2)
moto
→
v
r
p2
l
Q ∝Δp
Q = Δp/R
profilo della velocità
asse del
condotto
3
Q
parabolico
silenzioso
Resistenza
meccanica
di un condotto