I settori di PU sono controllati dall’autorità
pubblica
REGOLAMENTAZIONE
• Regolamentazione dell’entrata –
limiti all’accesso ai mercati
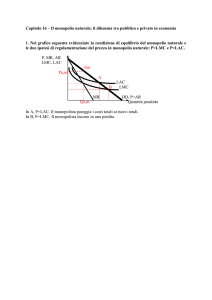
Settori di pubblica utilità
• Monopolio naturale
• Regolamentazione dei prezzi –
controllo delle tariffe e dei prezzi
• Servizi di rilievo sociale
Cambiamento degli assetti precedenti a partire
dagli anni ‘80
Assetto organizzativo industriale
• Imprese pubbliche controllate dallo stato
(Europa)
Non tutte le attività in un settore di PU sono
monopoli naturali
Vi sono attività potenzialmente concorrenziali
• Imprese private regolamentate (USA)
In Europa si è assistito ad un processo di privatizzazione e liberalizzazione
1
2
Ragioni del cambiamento
• Strutturali – progresso tecnologico consente
un minor grado di integrazione
• Politiche – Nuovi orientamenti di politica
economica
– Assetto integrato è meno efficiente
– Lo stato non deve produrre, ma regolare
la produzione privata
– Lo stato non deve perseguire obiettivi
impropri per mezzo delle imprese pubbliche
Occorrono strumenti di regolamentazione piú
sofisticati per
• Promuovere la concorrenza nei settori
liberalizzati
• Realizzare il coordinamento tra le varie componenti del settore
– Obiettivo della copertura universale ormai già raggiunto (o non perseguibile
mediante regolamentazione)
3
4
Funzione di costo sub-additiva
Monopolio naturale
L’intervento pubblico nei settori di pubblica
utilità è giustificato dalla presenza di condizioni
di monopolio ‘naturale’
Un Monopolio Naturale è un’industria in cui
per ragioni strutturali (tecnologia e domanda)
è ‘ottimale’ avere un unico produttore
Non si può promuovere la concorrenza, ma
soltanto controllare il potere di mercato del
monopolista (costi sociali del monopolio)
Definizione di monopolio naturale
n: numero di beni
q = (q1, q2, . . . , qn): vettore output
k ): vettore output impresa k
q k = (q1k , q2k , . . . , qn
C(q) : funzione di costo
C(q) è sub-additiva in q se
C(q) ≤
per ogni K > 1 e q =
K
C(q k )
k=1
k
kq
Il costo di produrre q con un’unica impresa è
inferiore al costo di produrre q con più imprese
Un’industria è un monopolio naturale se C(q)
è sub-additiva per tutti i valori di q ‘rilevanti’
data l’ampiezza del mercato
5
6
Caso multiprodotto (n = 2, 3, . . .)
Economie di scala e sub-additività
Caso monoprodotto (n = 1)
Come definire l’economie di scala?
Economie di scala: costi medi decrescenti; se
q > q allora C(q )/q < C(q)/q.
Elasticità di scala:
Se vi sono economie di scala la funzione di
costo è sub-additiva (e l’industria è un MN)
Dimostrazione:
poniamo q = k q k , quindi q k < q ...
La funzione di costo può essere sub-additiva
in un intervallo rilevante anche se non vi sono
economie di scala
σ(q) = n
C(q)
∂C(q)
i=1 qi ∂qi
σ(q) è il reciproco dell’elasticità del costo rispetto
a variazioni equiproporzionali dell’output
σ(q) > 1 : Economie di scala - i costi aumentano meno in percentuale rispetto all’output
σ(q) < 1 : Diseconomie di scala
N.B. Si possono avere economie di scala e una
funzione di costo non sub-additiva
Esempi: Grafici
7
8
Esempio (2 beni)
C(q1, q2) = q1α + q2α + (q1q2)β
con 0 < α < 1 e 0 < β < 1/2.
Si può mostrare che σ(q) > 1, quindi vi sono
economie di scala; tuttavia, C(q) non è subadditiva
C(q1, 0) + C(0, q2) = q1α + q2α < C(q1, q2)
Economie di diversificazione o varietà (Economies
of scope) (2 beni) se la funzione di costo soddisfa la condizione
C(q1, 0) + C(0, q2) > C(q1, q2)
La produzione congiunta comporta minori costi,
vi sono complementarietà di costo
Economie di scala e di diversificazione non implicano sub-additività
Costo incrementale per il bene 1
IC1(q1, q2) = C(q1, q2) − C(0, q2)
costo aggiuntivo per produrre il bene 1 quando
già si produce il bene 2
Vi sono complementarietà di costo tra i 2 beni
se
∂IC1(q1, q2)
<0
∂q2
cioè all ’aumentare di q2 si riduce il costo incrementale del bene 1
Nell’esempio precedente vi erano diseconomie
di diversificazione
9
10
SOSTENIBILITÀ
Costo medio incrementale del bene 1
IC1(q1, q2)
AIC1 =
q1
Un monopolista regolamentato non ha il controllo sui prezzi e, solitamente, opera in un
mercato ‘protetto’
Se AIC1 è decrescente (in q1) vi sono economie
di scala specifiche nella produzione del bene 1
Perché regolare l’entrata se vi sono condizioni
di monopolio naturale?
La funzione di costo è sub-additiva se vi sono
• costi medi incrementali decrescenti per ogni
bene
• economie di diversificazione (complementarietà di costo tra i beni)
Una configurazione di prezzi è ‘sostenibile’ se
rende non profittevole l’entrata di un concorrente a prezzi invariati
Se i prezzi regolamentati non sono ‘sostenibili’ possono entrare altre imprese nel mercato,
quindi occorre regolamentare l’entrata
Perche’ il regolamentatore fissa prezzi non sostenibili e regolamenta l’accesso?
11
12
Configurazioni dei prezzi
n numero di beni
m numero di imprese
q i output impresa i
p vettore dei prezzi
Q(p) domanda di mercato
Una configurazione (q1, . . . , qm; p) è sostenibile
se è ammissibile e se presi q̂ e p̂ tali che
p̂ ≤ p
Configurazione di mercato: (q1, q2, . . . , qm; p)
q̂ ≤ Q(p̂)
Una configurazione (q1, . . . , qm; p) è ammissibile
se
allora
p̂ · q̂ − C(q̂) ≤ 0
• c’è equilibrio tra domanda e offerta,
Q(p) = i qi
cioè non esiste un prezzo al quale un entrante
può servire il mercato (anche solo in parte) e
fare profitti positivi
• ogni impresa fa profitti non negativi,
p · q i − C(q i) ≥ 0
13
14
Sussidi incrociati
Configurazioni sostenibili in monopolio
• Una CS esiste soltanto se l’industria è un
monopolio naturale
Vi sono sussidi incrociati quando un mercato
in perdita viene finanziato da un mercato in
avanzo
Esempio: telefonia – servizi locali e servizi a
lunga distanza
• L’output è prodotto al minimo costo complessivo per l’industria
Una configurazione di prezzi non è sostenibile
se vi sono sussidi incrociati
• I profitti del monopolista sono pari a zero
Esempio 1.
Servizio di trasporto tra tre città: 1,2,3.
Tre collegamenti: a, b, c
• Il prezzo di ciascun bene è maggiore o uguale
al suo costo marginale, pi ≥ cmi
Una configurazione sostenibile è desiderabile
controllo del PdM – numero efficiente di produttori
15
2
...
...
...
..
...
...
...
...
.
.
..
...
...
..
...
...
...
...
...
...
...
.
.
...
...
...
...
...
..
...
...
...
...
.
.
..
...
...
..
...
...
...
...
...
...
...
.
..
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
a
1
b
.........................................................................................................................................................................................................................................................
c
3
16
Ricaviamo una configurazione di prezzi sostenibile (pa, pb, pc)
C(a) : costo linea ‘a’
C(ab) : costo linee ‘a’ e ‘b’
C(abc) : costo linee ‘a’, ‘b’ e ‘c’
Dal lato dei costi
• pa ≤ 10, pb ≤ 10 e pc ≤ 10
La domanda di trasporto su ciascuna linea è
rigida e pari a 1
• pa + pb ≤ 18, pa + pc ≤ 18 e pb + pc ≤ 18
• pa + pb + pc ≤ 24
Struttura dei costi
C(a) = C(b) = C(c) = 10
C(ab) = C(ac) = C(bc) = 18
C(abc) = 24
Dal lato della domanda
Diponibilità a pagare, Vi = 11 per ogni
i = a, b, c. Quindi pi ≤ Vi
La funzione di costo è sub-additiva, quindi il
settore è un monopolio naturale
Configurazione sostenibile (pa, pb, pc) = (8, 8, 8)
Configurazione NON sostenibile
pa < 6 e pb + pc > 18 (entrata in bc), esempio
di sussidio incrociato
17
18
Configurazioni senza sussidi incrociati
N : insieme dei mercati
S : sottoinsieme di mercati, S ⊆ N
N/S : mercati che non sono in S
C(S) : costo ‘stand alone’, costo minimo per
servire i mercati in S
Configurazione di prezzi senza sussidi incrociati
(subsidy-free)
i∈S
per ogni S
i∈N
pi ≤ C(S)
(1)
pi = C(N )
(2)
i∈S
pi ≥ C(N ) − C(N/S)
(3)
C(N )−C(N/S) è il costo incrementale di servire
i mercati in S. Quindi, in assenza di sussidi incrociati, i ricavi in ogni sottoinsieme di mercati
devono superare i costi incrementali
Dalla (1) e la (3)
C(N ) − C(N/S) ≤
i∈S
pi ≤ C(S)
Se il prezzo è inferiore al costo incrementale,
vi sono sussidi incrociati
Esempio 2.
pa < 6 e C(abc) − C(bc) = 24 − 18 = 6
Se valgono (1) e (2) è impossibile per un entrante fare profitti.
Dalla (2) si ha
La configurazione di prezzi senza sussidi incrociati è anche una configurazione di prezzi
sostenibile
i∈N pi = i∈S pi + i∈N/S pi = C(N )
e dalla (1)
19
20
Se vi sono sussidi incrociati, es. i∈s pi > C(S)
vi è un incentivo per un’impresa ad entrare nei
mercati in S.
Esempio 3.
Supponiamo Vc = 5. Una configurazione di
prezzi che garantisce il servizio su ‘a’, ‘b’ e
‘c’ e che assicura il pareggio di bilancio del
monopolista è
pc = 5
pa = pb = 9, 5
L’entrante può ‘scremare’ (cream skimming) il
mercato entrando nei mercati in cui il prezzo
è superiore al costo stand alone e lasciare al
monopolista i mercati in perdita
Queste tariffe non sono sostenibili, la tratta ‘c’
è sussidiata dalle linee ‘a’ e ‘b’
Esempio. Compagnia aerea nazionale – tratte
piú affollate e tratte meno affollate
In termini di benessere sociale la tratta ‘c’ dovrebbe
essere soppressa
Se un regolatore impone ad un monopolista
prezzi con sussidi incrociati (per ragioni di natura
distributiva) deve anche proteggere il mercato
e regolamentare l’entrata
Va + Vb + Vc − C(abc) = 27 − 24 = 3
e
Va + Vb − C(ab) = 22 − 18 = 4
Finalità redistributive
sussidi incrociati – altri strumenti ?
21
Non sempre esistono configurazioni
di prezzi sostenibili
22
Configurazione pa = pb = pc = 9
Non sostenibile (ab)
Tariffe non sostenibili possono rendersi necessarie per assicurare il pareggio di bilancio del
monopolista
Configurazione pa = pb = 8, 5 e pc = 10
Non sostenibile (ac)
Esempio 4.
Struttura dei costi
C(a) = C(b) = 10
C(c) = 11
C(ab) = 17
C(ac) = C(bc) = 18
C(abc) = 27
Questo settore è un monopolio naturale perché
la funzione di costo è sub-additiva. Tuttavia,
non esiste una configurazione di prezzi sostenibile
Costi incrementali
IC(a) = C(abc) − C(bc) = 27 − 18 = 9
IC(b) = C(abc) − C(ac) = 27 − 18 = 9
IC(c) = C(abc) − C(ab) = 27 − 17 = 10
Anche nel caso monoprodotto può non esistere
una configurazione sostenibile in presenza di
sub-additività dei costi
Se fissiamo i prezzi pari ai costi incrementali,
pa = pb = 9 e pc = 10 il monopolista fa profitti
positivi
Π = pa + pb + pc − C(abc) = 1
23
Grafico
Un entrante può sottrarre una parte del mercato al monopolista
24
In monopolio naturale in assenza di sostenibilità dei prezzi è necessario regolamentare
l’entrata o, in alcuni casi, vietare forme di
‘by-pass’ del monopolista
Esempio. Grande impresa che produce autonomamente energia per il proprio fabbisogno
(vedi grafico)
Incremento dei costi complessivi dell’industria
Condizioni di esistenza di una configurazione
sostenibile (caso più semplice con 2 beni e domande indipendenti)
In sintesi
I prezzi regolamentati possono non essere
sostenibili
• per ragioni di natura equitativa – sussidi
incrociati
• perché, in particolari condizioni, non
esistono prezzi sostenibili
∂Q2 ∂IC1(q1, q2)
≥0
∂p2
∂q2
Il problema della ‘protezione’ del monopolista
è articolato (vedi schema)
Sono necessarie complementarietà di costo.
25
26