Economia Pubblica
il Monopolio Naturale
Giuseppe De Feo
Università degli Studi di Pavia
email: [email protected]
Secondo Semestre 2011-12
Outline
il Monopolio Naturale
Il problema del Monopolio Naturale
Subadditività della funzione di costo
Politiche di prezzo ottimali
la regola del costo marginale
La regola del costo medio
prezzi à la Ramsey
Altri metodi di regolamentazione dei prezzi
Test sui sussidi incrociati
Prezzi non lineari
Il monopolio Naturale
I
Una prima definizione di monopolio naturale:
Un’industria è un monopolio naturale se il costo di produrre la
quantità venduta sul mercato è minimizzato quando una sola
impresa produce l’intera quantità piuttosto che due o più imprese.
I
Difficoltà di conciliare efficienza produttiva e efficienza allocativa.
Come si può ottenere di produrre al costo più basso senza essere
soggetti al potere di mercato del monopolista?
Il monopolio Naturale
si può introdurre la concorrenza?
Si consideri:
I
n imprese simmetriche
I
una funzione di costo Ci (qi ) = k + cqi tale che AC =
I
una funzione
di domanda inversa decrescente p(Q) con
Pn
Q = i=1 qi
k
qi
+c
Ipotizziamo il seguente gioco a due stadi in cui:
Stadio 1 Le imprese potenziali entranti decidono se entrare o
meno sul mercato (per entrare bisogna pagare il
costo fisso k, che è irrecuperabile se l’impresa esce
dal mercato)
Stadio 2 m imprese entrano sul mercato e competono
scegliendo simultaneamente il prezzo
(concorrenza à la Bertrand)
Il monopolio Naturale
si può introdurre la concorrenza?
Si risolva il gioco con l’induzione a ritroso per trovare l’E.P.S.
Stadio 2 (Concorrenza sul prezzo à la Bertrand)
I se m = 1: prezzo di monopolio
I se m ≥ 2: la concorrenza à la Bertrand porta a p = c e
Πi = −k
Stadio 1 (Decisione di entrata)
I se m ≥ 2 questa scelta non è un EPS perché le imprese
prefeririscono essere fuori dal mercato
I solo se m = 1 il risultato è un equilibrio in strategie pure.
In tal caso si ottiene efficienza produttiva ma potere
monopolistico (inefficienza allocativa).
I possono esistere equilibri in strategie miste con le imprese
che entrano con una certa probabilità. Se più imprese
entrano: efficienza allocativa, ma inefficienza produttiva.
Subadditività della funzione di costo
Una definizione più precisa di Monopolio Naturale
un’industria è un monopolio naturale se la funzione di costo è subadditiva
nell’intervallo di produzione rilevante
Cosa vuol dire?
Bisogna distinguere il caso dell’impresa monoprodotto da quello
dell’impresa multiprodotto
Impresa monoprodotto
La funzione di costo è subadditiva al livello Q se
C (Q) ≤ C (q1 ) + C (q2 ) ∀q1 , q2 : q1 + q2 = Q
Economie di scala ⇒ Subadditività
ma
Economie di scala : Subadditività
La produzione è caratterizzata da economie di scala se la funzione di
costo è tale che
C (tq) ≤ tC (q) con t > 1
Subadditività della funzione di costo
Rappresentazione grafica
Le funzioni di costo medio dell’industria con una o due imprese
Figure: AC è la funzione di costo medio quando un’impresa produce Q. AC2 è
il costo medio minimo quando due imprese producono Q.
I
Intervallo in cui esistono economie di scala: (0, Q 0 )
I
Intervallo in cui c’è subadditività: (0, Q ? )
Subadditività della funzione di costo
Impresa multiprodotto
I
Di solito le imprese producono più di un prodotto (per
esempio i servizi in orari di punta e non di punta sono due
prodotti diversi)
I
Si consideri un monopolista che produce i beni 1 e 2;
la funzione di costo è C (Q1 , Q2 )
Le seguenti difinizioni si applicano nel caso multiprodotto:
I
economie di scala: C (tQ1 , tQ2 ) ≤ tC (Q1 , Q2 ) con t > 1
I
economie di scopo: C (Q1 , Q2 ) ≤ C (Q1 ) + C (Q2 )
I
subadditività (a Q1 , Q2 ):
C (Q1 , Q2 ) ≤ C (q1a , q2a ) + C (q1b , q2b )
∀qij : qia + qib = Qi i = 1, 2
La subadditività dipende da entrambi i tipi di economie, ma
nessuna è necessaria o sufficiente.
Politiche di prezzo ottimali
Politiche di prezzo ottimali
I
i prezzi ottimi massimizzano il benessere sociale
I
in presenza di economie di scale di scopo vi sono problemi
nell’applicazione della regola prezzo = costo marginale
I
rilevanza di regole di prezzo di “second-best”
I
prezzi lineari e non lineari
I
considereriamo monopoli naturali monoprodotto e
multiprodotto
I
problemi di applicazione dei prezzi ottimi: problemi di
incentivo e di asimmetria informativa
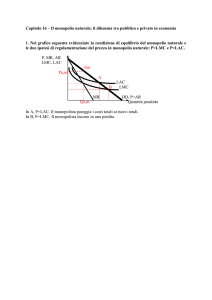
la regola di prezzo = costo marginale
I
se P = MC l’efficienza allocativa è massimizzata
I
ma vi sono perdite per l’impresa (area P0 STR)
I
l’impresa deve ricevere sussidi per continuare a produrre
la regola di prezzo = costo marginale
Se si devono usare i sussidi:
I
Tasse per per costituire i fondi necessari
ma sia tasse sul reddito che sui consumi causano perdite di
benessere (sono distorsive)
I
I
I
I
Le tasse indirette introducono un markup tra costi e prezzi
(proprio come i prezzi di monopolio)
Le tasse dirette distorcono le scelte di consumo degli individui
solo tasse in somma fissa non sono distorsive
ma ci sono molti argomenti contrari all’uso dei sussidi:
I
I
I
I
il costo totale può essere maggiore dei benefici totali
perché i fruitori di questo servizio devono essere sussidiati dai
non fruitori?
si favoriscono inefficienze produttive
è politicamente difficile introdurre sussidi a favore di monopoli
privati
La regola del costo medio
Una soluzione di second-best
massimizzazione del benessere sotto il vincolo di bilancio in
pareggio.
I
la soluzione è facile quando il monopolista è monoprodotto:
P = AC
I
c’è comunque una perdita di benessere
prezzi à la Ramsey
second-best per un monopolista multiprodotto
Q. come definire i prezzi in modo che i costi siano coperti e la perdita di
benessere sia minimizzata?
A. prezzi à la Boiteux-Ramsey
1. si consideri il problema di massimizzazione dei profitti di un
monopolista multiprodotto
max
n
X
pi qi − c (q1 , ..., qi , ..., qn )
i=1
Per la Condizione del Primo Ordine (FOC): MRi = ci0
Se le domande sono independenti: pi + qi pi0 = ci0 ⇒ pi −
dove ηi =
∂qi pi
− ∂p
i qi
pi
ηi
= ci0
è l’elasticità della domanda del bene i. Da cui:
pi − ci0
1
=
∀i
pi
ηi
prezzi à la Ramsey
2. i prezzi à la Ramsey-Boiteux sono la soluzione del seguente
problema:
max W (p1 , ..., pi , ..., pn )
pi
tale che
n
X
pi qi − c (q1 , ..., qi , ..., qn ) ≥ 0
i=1
Indichiamo con W RB il livello di benessere utilizzando i prezzi
soluzione del problema
prezzi à la Ramsey
3. Il problema precedente può anche essere riscritto in modo
duale
max
pi
n
X
pi qi − c (q1 , ..., qi , ..., qn )
i=1
tale che W (p1 , ..., pi , ..., pn ) ≥ W RB
È possibile dimostrare che la soluzione è la stessa:
pi − ci0
k
=
∀i
pi
ηi
Dove k < 1 è una costante
prezzi à la Ramsey
I
la struttura ottimale dei prezzi per un monopolio
regolamentato è la stessa di quella ottimale per un
monopolista non regolamentato
I
infatti il rapporto tra i markup è lo stesso in entrambi i casi ed
uguale al rapporto inverso delle elasticità della domanda
I
in parole povere: i prezzi à la Ramsey sono gli stessi di un
monopolista non regolamentato, solo più bassi
I
più inelastica è la domanda, più alti sarà il markup
se le domande dei beni non sono indipendenti:
I
I
I
i markup saranno più bassi per i beni complementari
i markup saranno più alti per i beni sostituti
prezzi à la Ramsey
Una regola molto semplice quando abbiamo costi e domanda
lineari:
qj pjRB
qi piRB
=
qi ci0
qj cj0
Cioè:
1. definire la quantità che equaglia il prezzo al costo marginale
per ciascun bene
2. ridurre la quantità proporzionalmente per entrambi i beni fino
a quando non si raggiunge il pareggio di bilancio
Esempio numerico:
c (q1 , q2 ) = 1800 + 20q1 + 20q2
q1 = 100 − p1
q2 = 120 − 2p2
prezzi à la Ramsey
Confronto tra aumento proporzionale dei prezzi e Ramsey
I
i prezzi à la Ramsey minimizzano la perdita di benessere in
presenza di un vincolo di bilancio
I
i prezzi sono più alti quanto più rigida è la domanda
Altri metodi di regolamentazione dei prezzi
Il metodo del costo permanente redistribuito è utilizzato
I
in presenza di più prodotti
I
o più gruppi di utenti
Si ipotizzi che:
I
costo di produzione del bene 1: c(q1 ) = 1250 + 20q1
I
costo di produzione del bene 2: c(q2 ) = 900 + 20q2
mentre
I
produzione congiunta: c (q1 , q2 ) = 1800 + 20q1 + 20q2
La funzione di costo è subadditiva.
I
l’allocazione del costo fisso avviene considerando una qualche
misura fisica, come il tempo di utilizzo degli impianti
Altri metodi di regolamentazione dei prezzi
si assuma che 75% del costo fisso si carica sul bene 1 e 25% sul
bene 2
I
AC 1 =
I
AC 2 =
1350
q1 + 20
450
q2 + 20
Date le funzioni di domanda
I
per il bene 1: q1 = 100 − p1
I
per il bene 2: q2 = 120 − 2p2
La copertura dei costi è assicurata da p=AC. ovvero:
1350
q1 + 20
0.5q2 = 450
q2 + 20
I
per il bene 1: 100 − q1 =
I
per il bene 2: 60 −
I
risultato: q1 = 55.81, p1 = 44.19; q2 = 66.46, p2 = 26.77
I
prezzi Ramsey è:q1 = 60, p1 = 40; q2 = 60, p2 = 30
I
inefficienza del metodo del costo redistribuito
sussidi incrociati
La regolamentazione effettiva del monopolio naturale è stata a
lungo lontana dai prezzi Ramsey
Esempio: le tariffe telefoniche sono state caratteirizzate da
I
prezzi utenze domestiche più bassi di quelle affari
I
tariffe urbane e interurbane
I
servizio universale
Obiettivi redistributivi e di sviluppo rurale invece dell’efficienza
I
sorgono problemi con le liberalizzazioni e la concorrenza
I
importante verificare la presenza di sussidi
test sui sussidi incrociati
Test sui sussidi incrociati
1. metodo del costo da solo (CDS)
Verifica se i ricavi su uno solo dei servizi superano i costi di offrire
il servizio stesso da solo
I
Si riprenda il caso del Costo Permanente Redistribuito
analizzato in precedenza
I
il test dimostra la presenza di sussidi incrociati
I
si consideri il caso dei prezzi alla Ramsey analizzato in
precedenza
I
il testo dimostra l’assenza di sussidi incrociati
test sui sussidi incrociati
Test sui sussidi incrociati
2. metodo del costo medio incrementale (AIC)
Verifica se i ricavi sono superiori o meno al costo aggiuntivo di
produrre il bene
I
Si riprenda il caso del Costo Permanente Redistribuito
analizzato in precedenza
c (q1 , q2 ) − c(q2 )
= 20 +
q1
c (q1 , q2 ) − c(q1 )
AIC2 =
= 20 +
q2
AIC1 =
900
= 36.13
q1
550
= 28.28
q2
I
poiché i prezzi sono p1 = 44.19; p2 = 26.77
I
il testo dimostra la presenza di sussidi incrociati
I
si consideri il caso dei prezzi Ramsey analizzato in precedenza
Prezzi non lineari
3. prezzi non lineari
Prezzi non lineari possono essere costruiti a partire da tariffe a due
parti:
I
una parte fissa (indipendente dal livello di consumo)
I
un parte variabile per unità consumata
Una politica ottimale potrebbe essere la seguente:
I
un prezzo = CM per la parte variabile
I
una parte fissa tale da coprire il costo fisso di produzione
Esempio:
se il costo fisso è = K e ci sono N consumatori, allora potrebbe
essere ottimale definire una parte fissa della tariffa = K
N
Prezzi non lineari
Possibili problemi con una tariffa a due parti:
I
alcuni consumatori posso uscire dal mercato per non pagare la
parte fissa della tariffa
I
i consumatori possono formare gruppi e risparmiare sui costi
fissi
una possibile soluzione al primo problema:
I
discriminazione: parte fissa diversa per diversi gruppi di
consumatori
potrebbe essere proibita.
Comunque, la tariffa a dua parti può far meglio dei prezzi lineari.
Riduce la distorsione di P > CM
se nessuno abbandona il mercato: ottimo di primo rango (Tariffa di
Coase)
Prezzi non lineari
Un tariffa a due parti può bilanciare
I
perdite dovute alla parte fissa (consumatori che escono dal
mercato)
I
perdite dovute alla parte variabile P > MC (perdita netta di
surplus)
con risultati migliori dei prezzi Ramsey: non vincolata a tariffe
lineari.
Un esempio dall’industria telefonica:
Tariffe decrescenti a blocchi
I
un costo fisso al mese di 5 euro
I
+ 10c per chiamata fino a 100 chiamate
I
+ 5c per chiamata per tutte le chiamate tra 100 e 200
I
gratuite tutte le chiamate oltre le prime 200
Prezzi non lineari
Prezzi marginali decresenti
La spesa totale dei consumatori è ABCD
Motivazioni economiche:
I
Incentivi per sfruttare economie di scala
I
strumento per discriminare tra consumatori (discriminazione
di secondo grado)
Prezzi non lineari
I
è equivalente al seguente menu di tariffe a 2 parti:
I
I
I
5 euro di parte fissa + 10c di prezzo unitario
10 euro di parte fissa + 5c di prezzo unitario
20 euro di parte fissa + 0c di prezzo unitario
I
l’ottimo sociale sarebbe: nessun escluso e P = CM
I
la tariffazione a più parti è la migliore approssimazione senza
conoscere le preferenze individuali
I
I
definisce un meccanismo di autoselezione
e serve in presenza di asimmetrie informative