Traslazioni: Attività 1
I. Equazioni di una traslazione
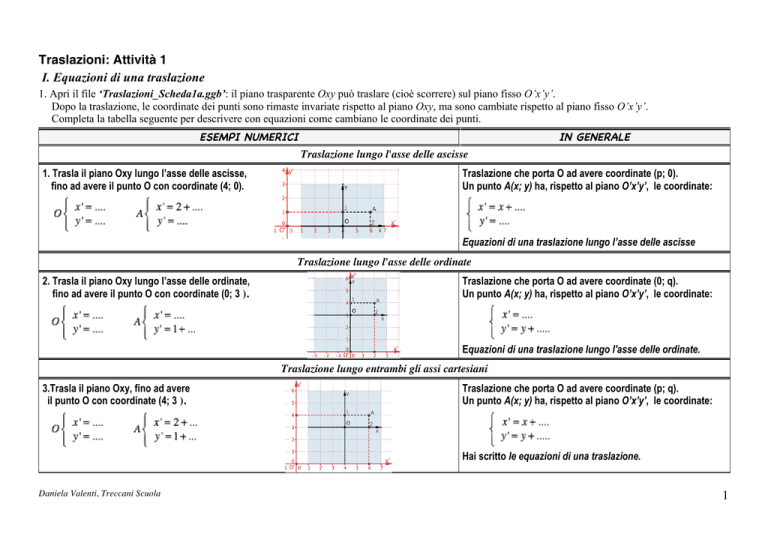
1. Apri il file ‘Traslazioni_Scheda1a.ggb’: il piano trasparente Oxy può traslare (cioè scorrere) sul piano fisso O’x’y’.
Dopo la traslazione, le coordinate dei punti sono rimaste invariate rispetto al piano Oxy, ma sono cambiate rispetto al piano fisso O’x’y’.
Completa la tabella seguente per descrivere con equazioni come cambiano le coordinate dei punti.
ESEMPI NUMERICI
IN GENERALE
Traslazione lungo l'asse delle ascisse
1. Trasla il piano Oxy lungo l’asse delle ascisse,
fino ad avere il punto O con coordinate (4; 0).
Traslazione che porta O ad avere coordinate (p; 0).
Un punto A(x; y) ha, rispetto al piano O’x’y’, le coordinate:
Equazioni di una traslazione lungo l’asse delle ascisse
Traslazione lungo l'asse delle ordinate
2. Trasla il piano Oxy lungo l’asse delle ordinate,
fino ad avere il punto O con coordinate (0; 3 ).
Traslazione che porta O ad avere coordinate (0; q).
Un punto A(x; y) ha, rispetto al piano O’x’y’, le coordinate:
Equazioni di una traslazione lungo l'asse delle ordinate.
Traslazione lungo entrambi gli assi cartesiani
3.Trasla il piano Oxy, fino ad avere
il punto O con coordinate (4; 3 ).
Traslazione che porta O ad avere coordinate (p; q).
Un punto A(x; y) ha, rispetto al piano O’x’y’, le coordinate:
Hai scritto le equazioni di una traslazione.
Daniela Valenti, Treccani Scuola
1
II. Trasformare poligoni con le equazioni di una traslazione
2. In un piano Oxy è dato il triangolo che ha per vertici i punti A(0; 4), B(4; 4), C(1; 1)
Il piano Oxy viene traslato fino ad avere O con coordinate (3; −2).
a. Completa le equazioni della traslazione
b. Completa qui sotto il procedimento per determinare i vertici del triangolo trasformato.
Il triangolo trasformato ha i vertici con le coordinate seguenti:
c. Disegna qui a fianco, nel piano Ox’y’,
- il triangolo iniziale ABC;
- il punto O e il triangolo A’B’C’ ottenuti dopo la traslazione.
III. Descrivere una traslazione con un vettore
3. Risolvi i seguenti quesiti.
a. Disegna qui sopra, nel piano Ox’y’, i segmenti orientati che congiungono ogni punto con il suo trasformato, ad esempio A con A’ (orientato verso A’).
b. Quale vettore v descrive la traslazione?
________________________________________________________________________________________________________________________
c. Scrivi qui a fianco le componenti cartesiane del vettore v. _________________________________________________________________________
IV. Trasformare poligoni con un software di geometria dinamica
4. Apri il file ‘Traslazioni_Scheda1b.ggb’; troverai disegnato il triangolo ABC e il punto O dati
nell’attività 2. Procedi nel modo seguente:
• Esplora il comando ‘Disegna un vettore’ per disegnare il vettore v da O’ verso O.
• Esplora il comando ‘Traslazioni’ per trasformare il triangolo ABC con la traslazione descritta
dal vettore v.
• Muovi liberamente i punti A, B e C per osservare le figure ottenute.
• Modifica liberamente il vettore per osservare le figure ottenute. In particolare che cosa succede se il vettore diventa parallelo all’asse delle ascisse o
all’asse delle ordinate? _____________________________________________________________________________________________________
________________________________________________________________________________________________________________________
Daniela Valenti, Treccani Scuola
2












