In geometria le figure si concepiscono come rigide, per cui è
possibile “muoverle” nello spazio senza che subiscano alcuna
deformazione.
La traduzione matematica dell’idea di movimento rigido di una
figura è una isometria, cioè una corrispondenza biunivoca del
piano in sé, che trasforma:
•segmenti in segmenti
•rette in rette
•angoli in angoli
L’isometria preserva le misure, il parallelismo, la
perpendicolarità; in tali trasformazioni varia invece la
“posizione” della figura nello spazio.
Tra tutti i movimenti rigidi delle figure piane quelle che in
studieremo sono:
Il concetto di simmetria,
riveste una fondamentale
importanza nello studio delle
configurazioni geometriche.
Simmetria, ordine, regolarità
sono le idee chiave di tutte le
discipline scientifiche.
Due punti simmetrici rispetto
all'asse x hanno la stessa
ascissa e le ordinate opposte
cioè: P(x,y) e P'(x,-y) Due
punti simmetrici rispetto
all'asse delle y ordinate hanno
ascisse opposte e stesse
ordinate P(x,y)= P(-x,y).
Due punti simmetrici rispetto
all'origine hanno opposte sia
l'ascisse che le ordinate P(x,y)
Simmetrico
rispetto asse y
P(-4,3)
cambia solo il
segno della
coordinata x
Simmetrico
rispetto all’origine
P(-4,-3)
cambia il segno
della coordinata x
ed y
P(4,3)
Simmetrico
rispetto asse x
P(4,-3)
cambia solo il
segno della
coordinata y
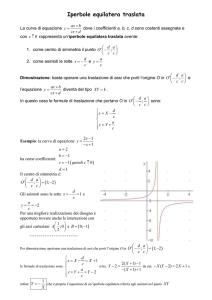
La traslazione è un movimento rigido che fa
coincidere per sovrapposizione due figure.
y
Come si vede dalla figura possiamo portare il
triangolo ABC a coincidere per
“sovrapposizione” con il triangolo A’B’C’,
facendo “scivolare” la figura sul piano in
modo che i vertici scorrano su linee parallele.
A
C
B
I segmenti paralleli AA’; BB’ ; CC’ sono di
uguale lunghezza
X
A’
Se analizziamo la traslazione vediamo che
può essere scomposta in due spostamenti
uno orizzontale ed uno verticale.
Chiameremo questi due valori
componente orizzontale e componente
verticale della traslazione
Spostamento
verticale
C’
B’
Spostamento
orizzontale
In generale una traslazione di componente orizzontale h e
componente verticale k ha equazione: x’=x+h
y’=y+k
Ogni traslazione è caratterizzata da tre elementi: ampiezza, direzione e verso
AMPIEZZA: l’ampiezza di una traslazione è la distanza tra un punto qualsiasi e il suo
trasformato
ampiezza della traslazione tr(h,k)= h2 + k2
l’ampiezza essendo una distanza ha sempre valore positivo.
DIREZIONE: Per una traslazione di componenti h e k con h= 0 è data dal rapporto:
k
h
VERSO: Ogni direzione individua due versi ( i due versi di percorrenza di una retta)
Il verso di una traslazione e determinato dalle due componenti h,k.
Esercizio svolto
Consideriamo il triangolo di vertici A(1,2) B(4,2) C(1,4) e il suo trasformato per
traslazione A’(-4,-4) B’(-1,-4) C’(-4,-2). Determinare: equazione della traslazione,
ampiezza direzione e verso.
Per determinare l’equazione della
traslazione dobbiamo tenere presente che
la componente orizzontale h è data dalla
differenza tra l’ascissa di un punto del
triangolo trasformato e quello
corrispondente sul triangolo dato:
h=Ax’-Ax= - 4 -1= - 5
analogamente per trovare l’ordinata
faremo la differenza tra le ordinate:
K=By’-By= - 4 - 2 = - 6
Una volta trovata la componente orizzontale e quella verticale avremo che l’equazione
della traslazione è: x’= x-5 y’= y - 6
l’ampiezza sarà (-5)2 + (-6) 2 = 7,8
la direzione è individuata dal rapporto 6/5
Le proprietà delle traslazioni
1. Una traslazione determina una corrispondenza biunivoca
del piano su se stesso
2. Una traslazione conserva la distanza tra due punti (è un movimento rigido)
3. Una traslazione porta ogni retta in una retta ad essa parallela
Cliccando sul tasto EXCEL vedrai come utilizzando
il foglio elettronico è semplice
eseguire la traslazione di un triangolo
note le sue coordinate e assegnata la traslazione tr(h,k)
Relazione tra due insiemi: ad ogni elemento del primo
insieme corrisponde uno ed uno solo elemento del secondo
insieme