Compito 4/3/99
pagina 1
Meccanica Applicata alle Macchine
compito del 4/3/99
A) Chi deve sostenere l'esame del I° modulo deve svolgere i punti 1 e 2.
B) Chi deve sostenere l'esame completo deve svolgere i punti 1, 2 e 3.
C) Chi deve sostenere l'esame del II° modulo deve svolgere i punti 3 e 4.
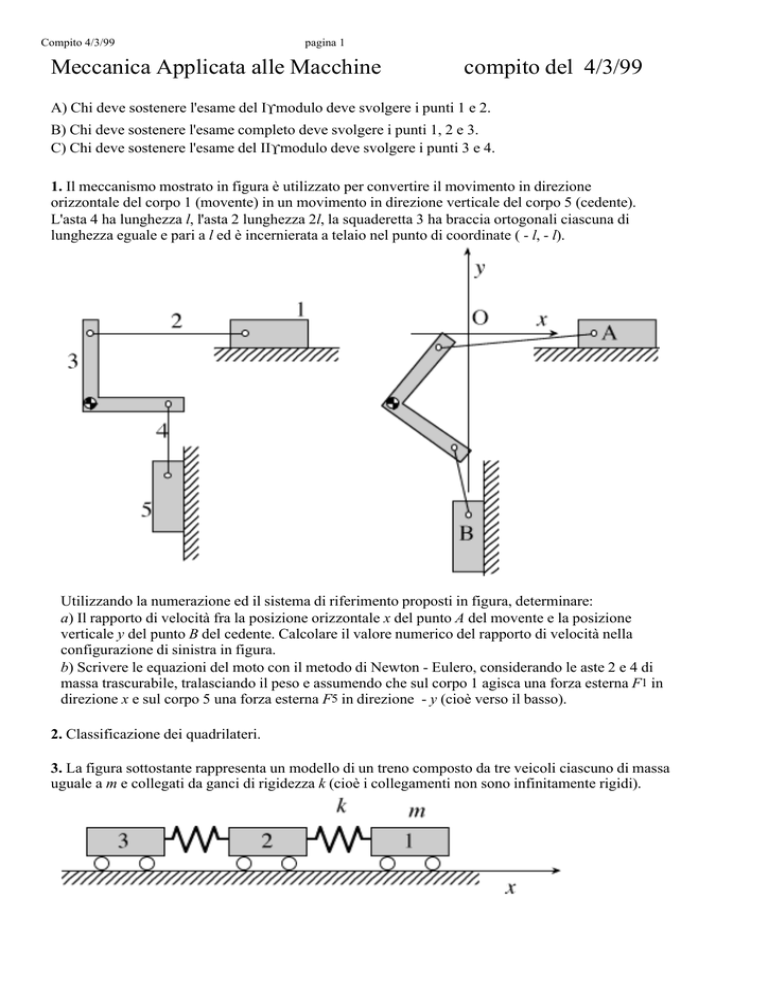
1. Il meccanismo mostrato in figura è utilizzato per convertire il movimento in direzione
orizzontale del corpo 1 (movente) in un movimento in direzione verticale del corpo 5 (cedente).
L'asta 4 ha lunghezza l, l'asta 2 lunghezza 2l, la squaderetta 3 ha braccia ortogonali ciascuna di
lunghezza eguale e pari a l ed è incernierata a telaio nel punto di coordinate ( - l, - l).
Utilizzando la numerazione ed il sistema di riferimento proposti in figura, determinare:
a) Il rapporto di velocità fra la posizione orizzontale x del punto A del movente e la posizione
verticale y del punto B del cedente. Calcolare il valore numerico del rapporto di velocità nella
configurazione di sinistra in figura.
b) Scrivere le equazioni del moto con il metodo di Newton - Eulero, considerando le aste 2 e 4 di
massa trascurabile, tralasciando il peso e assumendo che sul corpo 1 agisca una forza esterna F1 in
direzione x e sul corpo 5 una forza esterna F5 in direzione - y (cioè verso il basso).
2. Classificazione dei quadrilateri.
3. La figura sottostante rappresenta un modello di un treno composto da tre veicoli ciascuno di massa
uguale a m e collegati da ganci di rigidezza k (cioè i collegamenti non sono infinitamente rigidi).
Compito 4/3/99
pagina 2
a) Determinare le frequenze naturali e modi di vibrare del sistema.
b) Spiegare il significato fisico del modo corrispondente a frequenza zero.
c) Trovare il moto che segue alla applicazione di un impulso che impone velocità iniziale v0 al carro
di sinistra (gli altri carri sono inizialmentre in quiete).
Per risolvere il punto c utilizzare coordinate relative, cioè esprimere gli spostamenti dei carri 1 e 2
relativamente al carro 3 nel modo seguente (come risultano le equazioni in coordinate relatiive?):
x 1 = x 3+ y 1
x 2 = x 3+ y 2
4. Risposta di sistemi a un grado di libertà a forzanti di tipo periodico.












