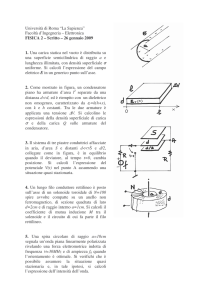
Tra le armature di un condensatore cilindrico di altezza h e di raggio interno R 1 ed esterno R2, tra le quali è applicata una ddp
pari a V, è presente un dielettrico di costante dielettrica
carica libera sulla armature. Si ricordi che
kV
, dove r è la distanza dall’asse. Si calcoli il modulo della
. Si eseguano i calcoli per : R1= 5cm, R2=20 cm , h=80 cm, V=1
Ponendo Qlib=Q, si ottiene che scegliendo una superficie Σ cilindrica di asse coincidente con quello del condensatore e raggio
,
. Dato che
. La ddp tra le armature è allora
, da cui
.
Q=5.9 10-8 C
Una spira circolare orizzontale di raggio L è concentrica con un filo conduttore verticale al quale è
connessa da una resistenza R. Incernierata sul filo, ruota senza attrito con velocità angolare costante
ω0, una sbarra metallica di lunghezza pari al raggio della spira con la quale è in contatto per mezzo
di un contatto strisciante. La spira è immersa in un campo magnetico verticale il cui modulo è
B=B0r, dove r è la distanza dal filo. Calcolare la potenza dissipata in R . Si eseguono i calcoli per
ω0= 5 rad/s, R=5 Ω, B0= 2 T/m e L=60 cm.
A regime il campo elettrico sulla sbarra è
e quindi
R
0
L
, con r generica distanza dal filo. Risulta allora che
i=0.14 A;
P i 2 R 0.098 W
Su un guscio sferico di raggio r è presente una carica che varia nel tempo secondo la legge Q=Q 0cosωt in modo quasi stazionario. Si calcoli:
a) l’espressione della corrente di spostamento in un punto R2>r; b) l’espressione del campo magnetico nello stesso punto.
Il problema si risolve considerando un circuito circolare di Raggio R2 e calcolando il flusso su una superficie che ha come contorno detto
circuito. Tale superficie può essere una semi sfera di raggio R2
a)
⃗
(
b)
)
da cui
Misurando il peso p in kg di 100 provini di una particolare lega prodotti da una stessa macchina, si ottengono i seguenti risultati distribuiti
secondo una distribuzione normale: 60≤p≤62, 5 provini; 63≤p≤65, 18; 66≤p≤68, 42; 69≤p≤71, 27 e 72≤p≤74, 8. Trovare gli intervalli di
confidenza al 95% e 99% del peso medio dei provini.
Per la stima del valore vero e della varianza si ottiene ̅
Ricordando che ̅
√
̅
.
Nel caso del 99%, t=2.576 e quindi
√
;
.
, al 95% corrisponde t=1.96 (dato che F(1.96)=0.975), da cui l’intervallo di confidenza è