Università di Roma “La Sapienza”
Facoltà d’Ingegneria – Elettronica
FISICA 2 – Scritto – 26 gennaio 2009
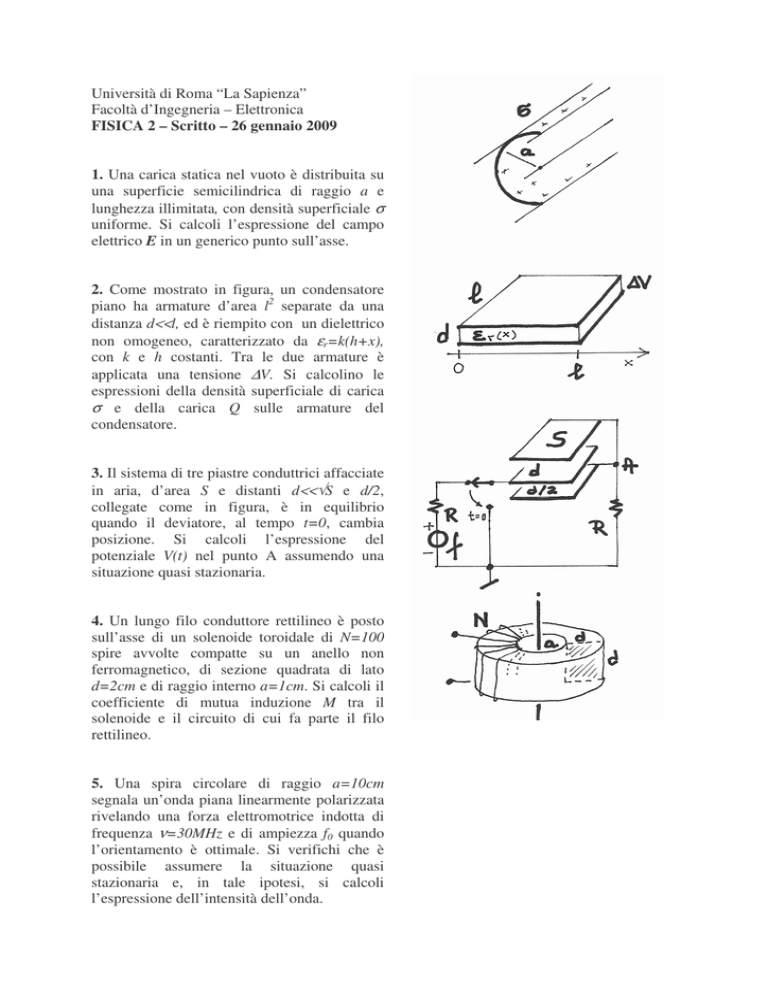
1. Una carica statica nel vuoto è distribuita su
una superficie semicilindrica di raggio a e
lunghezza illimitata, con densità superficiale σ
uniforme. Si calcoli l’espressione del campo
elettrico E in un generico punto sull’asse.
2. Come mostrato in figura, un condensatore
piano ha armature d’area l2 separate da una
distanza d<<l, ed è riempito con un dielettrico
non omogeneo, caratterizzato da εr=k(h+x),
con k e h costanti. Tra le due armature è
applicata una tensione ∆V. Si calcolino le
espressioni della densità superficiale di carica
σ e della carica Q sulle armature del
condensatore.
3. Il sistema di tre piastre conduttrici affacciate
in aria, d’area S e distanti d<<√S e d/2,
collegate come in figura, è in equilibrio
quando il deviatore, al tempo t=0, cambia
posizione. Si calcoli l’espressione del
potenziale V(t) nel punto A assumendo una
situazione quasi stazionaria.
4. Un lungo filo conduttore rettilineo è posto
sull’asse di un solenoide toroidale di N=100
spire avvolte compatte su un anello non
ferromagnetico, di sezione quadrata di lato
d=2cm e di raggio interno a=1cm. Si calcoli il
coefficiente di mutua induzione M tra il
solenoide e il circuito di cui fa parte il filo
rettilineo.
5. Una spira circolare di raggio a=10cm
segnala un’onda piana linearmente polarizzata
rivelando una forza elettromotrice indotta di
frequenza ν=30MHz e di ampiezza f0 quando
l’orientamento è ottimale. Si verifichi che è
possibile assumere la situazione quasi
stazionaria e, in tale ipotesi, si calcoli
l’espressione dell’intensità dell’onda.
Università di Roma “La Sapienza” - Facoltà d’Ingegneria
Soluzioni della prova scritta di Fisica II del 26 Gennaio 2009
1
dλ
~ = x̂Ex
Per simmetria E
a
dEx =
dEx
σ
θ
σ
Ex =
2πε0
~
dE
Z
σadθ
dλ
cos θ =
cos θ
2πε0 a
2πε0 a
+π/2
σ
σ
+π/2
[sin θ]−π/2 =
2πε0
πε0
cos θdθ =
−π/2
2
∆V
D
σ
εr ε0 ∆V
E=
,E=
= −→ σ =
d
ε
ε
d
Q=
Z
ε0 ∆V
σdS =
d
Z
ℓ
0
ε0 ∆V kℓ
k(h+x)ℓdx =
d
ℓ2
hℓ +
2
C
R
3
-Q 0
+Q 0
A
A
V(t)
-Q(t)
+
f
2C
R
+Q(t)
CP
R
Sia C = ε0 S/d e Cp = C + 2C = 3ε0 S/d,
V (t) =
−Q(t)
Q0
= − e−t/τ = −f e−t/τ
Cp
Cp
con τ = R
3ε0 S
.
d
4
Sia dS = d dr l’elemento infinitesimo di superficie della sezione quadrata del solenoide a distanza
r dal filo con r ∈ [a, a + d],
Z
Z a+d
Nµ0 d
a+d
µ0 I
· I = MI.
Φ=
BdS = N
d dr =
ln
2πr
2π
a
sez.
a
M=
102 · 4π10−7 · 2 10−2
ln 3 ≃ 4 10−7H = 0.4 µH.
2π
5
λ = c/ν =
3 108
= 10m ≫ 10cm
3 107
dB
f0
f0
f0 c
dB
S −→
= − sin (ωt) −→ B =
cos (ωt) −→ E0 =
−→ I =
f0 sin (ωt) = −
dt
dt
S
ωS
ωS
f0 c
2πνS
2
1
2Z0












