Disequazioni razionali

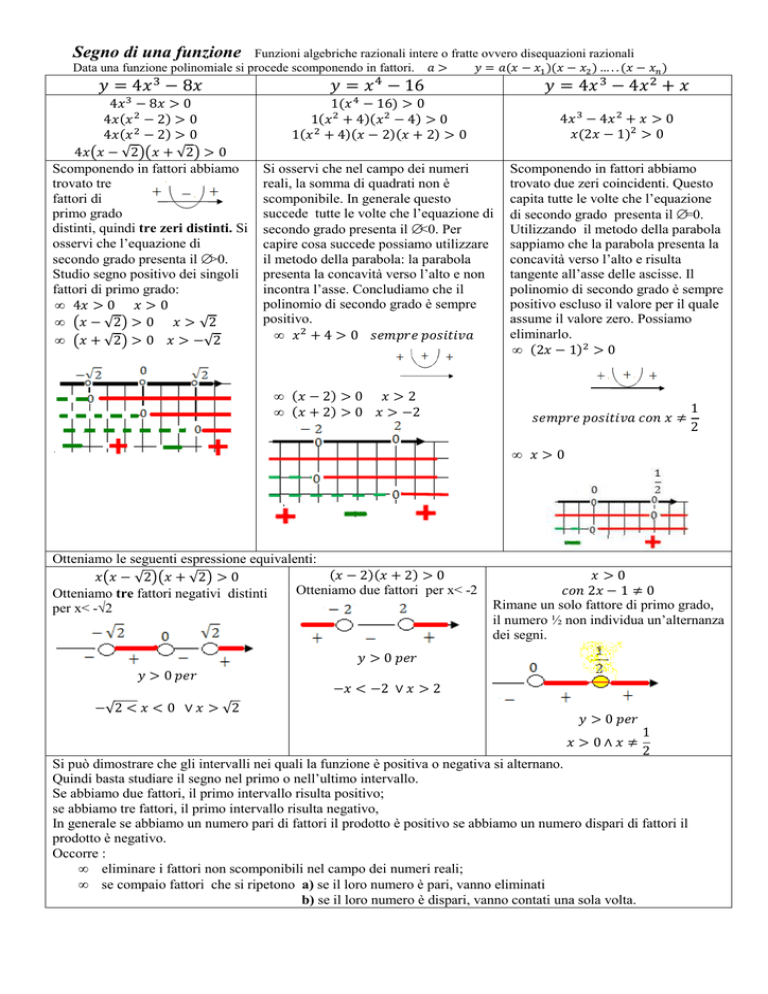
Segno di una funzione
Funzioni algebriche razionali intere o fratte ovvero disequazioni razionali
Data una funzione polinomiale si procede scomponendo in fattori. … . . 4 8
4 8 0
4 2
0
4 2
0
4 √2 √2 0
Scomponendo in fattori abbiamo
trovato tre
fattori di
primo grado
distinti, quindi tre zeri distinti. Si
osservi che l’equazione di
secondo grado presenta il ∆>0.
Studio segno positivo dei singoli
fattori di primo grado:
• 4 0 0
• √2 0 √2
• √2 0 √2
16
4 4 1 16
0
1 4
4
0
1 4
2
2
0
4 4 0
2 1
0
Si osservi che nel campo dei numeri
reali, la somma di quadrati non è
scomponibile. In generale questo
succede tutte le volte che l’equazione di
secondo grado presenta il ∆<0. Per
capire cosa succede possiamo utilizzare
il metodo della parabola: la parabola
presenta la concavità verso l’alto e non
incontra l’asse. Concludiamo che il
polinomio di secondo grado è sempre
positivo.
• 4 0 !"!#
• 2
0 2
• 2
0 2
Scomponendo in fattori abbiamo
trovato due zeri coincidenti. Questo
capita tutte le volte che l’equazione
di secondo grado presenta il ∆=0.
Utilizzando il metodo della parabola
sappiamo che la parabola presenta la
concavità verso l’alto e risulta
tangente all’asse delle ascisse. Il
polinomio di secondo grado è sempre
positivo escluso il valore per il quale
assume il valore zero. Possiamo
eliminarlo.
• 2 1
0
!"!# $ % &
1
2
• 0
Otteniamo le seguenti espressione equivalenti:
2
2
0
√2 √2 0
Otteniamo
due fattori per x< -2
Otteniamo tre fattori negativi distinti
per x< -√2
0
$ % 2 1 & 0
Rimane un solo fattore di primo grado,
il numero ½ non individua un’alternanza
dei segni.
0 0 √2 ' ' 0 ( √2
' 2 ( 2
0 0) &
1
2
Si può dimostrare che gli intervalli nei quali la funzione è positiva o negativa si alternano.
Quindi basta studiare il segno nel primo o nell’ultimo intervallo.
Se abbiamo due fattori, il primo intervallo risulta positivo;
se abbiamo tre fattori, il primo intervallo risulta negativo,
In generale se abbiamo un numero pari di fattori il prodotto è positivo se abbiamo un numero dispari di fattori il
prodotto è negativo.
Occorre :
• eliminare i fattori non scomponibili nel campo dei numeri reali;
• se compaio fattori che si ripetono a) se il loro numero è pari, vanno eliminati
b) se il loro numero è dispari, vanno contati una sola volta.
a<0
se il coefficiente del termine di grado massimo è negativo occorre conteggiarlo nel numero dei fattori.
4 8
16
4 4 4 8 0
4 2
0
4 2
0
4 √2 √2 0
1 16
0
1 4
4
0
1 4
2
2
0
4 4 0
12 1
0
• a<0 sempre -4<0
• 0 0
• √2 0 √2
• √2 0 √2
• a<0 sempre negativa -4<0
• 4 0
!"!#
• 2
0 2
• 2
0 2
Otteniamo le seguenti espressione equivalenti:
2
2
0
√2 √2 0
0
quattro fattori negativi per x< -√2
0 2 ' ' 2
• a<0 sempre negativa -4<0
• 2 1
0
!"!# $ % &
• 0
0
$ % 2 1 & 0
0 '0
0 ' √2 ( 0 ' ' √2
Si può dimostrare che gli intervalli nei quali la funzione è positiva o negativa si alternano.
Quindi basta studiare il segno nel primo o nell’ultimo intervallo.
Se abbiamo due fattori, il primo intervallo risulta positivo;
se abbiamo tre fattori, il primo intervallo risulta negativo,
In generale se abbiamo un numero pari di fattori il prodotto è positivo se abbiamo un numero dispari di fattori il prodotto è negativo.
Occorre :
•
eliminare i fattori non scomponibili nel campo dei numeri reali;
•
se compaio fattori che si ripetono a) se il loro numero è pari, vanno eliminati
b) se il loro numero è dispari, vanno contati una sola volta.
1
2