E' più probabile che sia pari o dispari?
Siano a e b due numeri reali presi uniformemente tra 0 ed 1. Sia x l'intero più vicino al
rapporto a/b.
E' più probabile che x sia pari o dispari?
________________________________________________________________
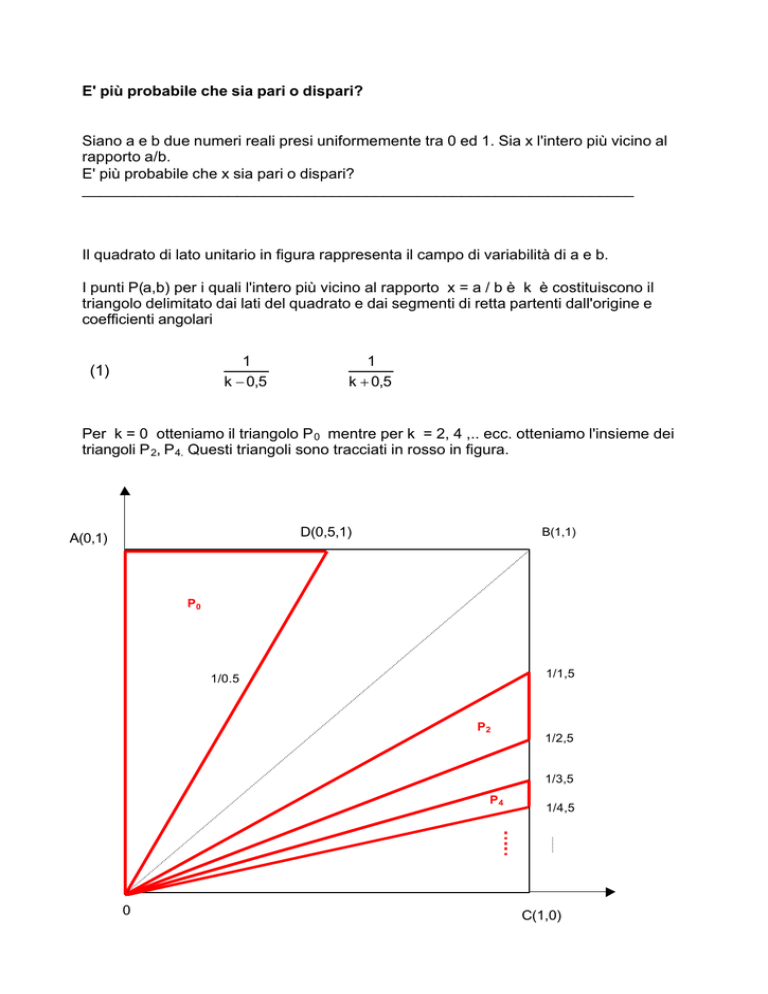
Il quadrato di lato unitario in figura rappresenta il campo di variabilità di a e b.
I punti P(a,b) per i quali l'intero più vicino al rapporto x = a / b è k è costituiscono il
triangolo delimitato dai lati del quadrato e dai segmenti di retta partenti dall'origine e
coefficienti angolari
1
k − 0,5
(1)
1
k + 0,5
Per k = 0 otteniamo il triangolo P 0 mentre per k = 2, 4 ,.. ecc. otteniamo l'insieme dei
triangoli P 2, P4. Questi triangoli sono tracciati in rosso in figura.
D(0,5,1)
A(0,1)
B(1,1)
P0
1/1,5
1/0.5
P2
1/2,5
1/3,5
P4
0
1/4,5
C(1,0)
La probabilità Pp che l'intero più vicino a x sia pari è data dal rapporto tra la somma
delle aree dei triangoli P 0, P 2 ,P4… ecc. e l'area del quadrato di lato unitario.
Osserviamo che tutti i triangoli interessati hanno altezza unitaria, per cui la somma delle
loro aree è data dalla metà della somma delle basi. E' quindi
(2)
1 1 1
1 1
1 1
1
Pp = +
−
−
−
+
+
+ .....
2 2 1,5 2,5 3,5 4,5 5,5 6,5
(3)
Pp =
1
1 1 1 1 1
1
+ 1− 1 − + − + − +
− ...
4
3 5 7 9 11 13
(4)
Pp =
5 −ð
= 0,4646018
4
essendo la serie tra parentesi nella (3) convergente e con somma π/4.
La probabilità Pd che l'intero più vicino a x sia dispari è
(5)
Pd = 1 − Pp =
ð -1
= 0,5353981
4
E' quindi più probabile che x sia dispari.