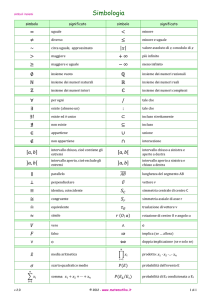
Funzioni continue
Dal punto di vista intuitivo dire che una funzione è continua in un intervallo è come dire che nel
disegnare il suo grafico non stacchiamo mai la penna dal foglio.
Scriviamo adesso la definizione rigorosa di continuità in un punto:
Sia f (x) una funzione definita in un intorno di x 0 .
La funzione si dice continua nel punto x 0 quando esiste il limite di f (x) per
limite è uguale al valore f ( x 0) della funzione calcolata in x 0 , ovvero:
x → x 0 e tale
lim f ( x )=f ( x 0)
x →x 0
In sostanza questo significa che affinché una funzione sia continua in un punto
verificate tre condizioni:
x0
devono essere
1. deve esistere il valore della funzione nel punto x 0 (cioè deve essere possibile calcolare
f (x 0) e questo numero deve essere finito);
2. deve esistere il limite della funzione per x tendente a x 0
3. il valore di questo limite deve coincidere con f (x 0)
Se anche una sola di queste condizioni non è verificata allora la funzione non è continua nel punto
x 0 (in questi casi si dice che è discontinua nel punto x 0 )
Una prima immediata conseguenza della definizione è che se x 0 non appartiene al dominio della
funzione, la funzione stessa è discontinua nel punto x 0 . Infatti, se x 0 non appartiene al
dominio, non possiamo calcolare f (x 0) perché esso non esiste.
Esempio1:
y=
1
. Il dominio è D: R-{0}
x
La funzione è discontinua nel punto x=0 perché il valore della funzione nel punto 0 (cioè
non esiste.
page 1/5
f (0) )
Esempio 2:
Dal grafico si vede immediatamente che questa funzione è discontinua nel punto x=3.
Analizziamo ora, per quanto riguarda questo esempio, la definizione rigorosa di continuità in un
punto:
1) deve esistere il valore della funzione nel punto f ( x 0) . Nel nostro caso
f (3)=2 (pallino pieno). Questa condizione è quindi soddisfatta.
x 0 =3 e
2) Deve esistere il limite della funzione per x tendente a x 0 . Nel nostro caso x 0 =3 e
lim f ( x)=1 . Sia il limite destro che il limite sinistro esistono ed entrambi valgono 1.
x→ 3
(Infatti, se x si avvicina a 3, sia da destra che da sinistra, la funzione si avvicina a 1). Anche
questa condizione è quindi soddisfatta.
3) Il valore del limite deve coincidere con f ( x 0) . Nel nostro caso il limite è 1 mentre
f (3)=2 . Questa condizione non è soddisfatta. La funzione è quindi discontinua nel
punto x=3
page 2/5
Esempio 3
Questa funzione è simile a quella di prima ma è diversa. Essa è infatti continua nel punto x=3.
Vediamo perché:
1) deve esistere il valore della funzione nel punto
f (3)=1 Questa condizione è quindi soddisfatta.
x 0 . Nel nostro caso
x 0 =3 e
2) Deve esistere il limite della funzione per x tendente a x 0 . Nel nostro caso x 0 =3 e
lim f ( x)=1 . Sia il limite destro che il limite sinistro esistono ed entrambi valgono 1.
x→ 3
(Infatti, se x si avvicina a 3, sia da destra che da sinistra, la funzione si avvicina a 1). Anche
questa condizione è soddisfatta.
3) Il valore del limite deve coincidere con
f (3)=1.
f ( x 0) . Nel nostro caso il limite è 1 e
La funzione è quindi continua nel punto x=3
Continuità in un intervallo
Se la funzione risulta continua in ogni punto di un certo intervallo allora diciamo che la funzione è
continua in quell'intervallo.
L'intervallo può essere anche tutto R. In questo caso diciamo che la funzione è continua in R.
page 3/5
Nell'esempio 1: la funzione è continua ovunque tranne che in x=0
Nell'esempio 2: la funzione è continua per tutti i punti del suo intervallo di definizione tranne che
nel punto x=3.
Nell'esempio 3: la funzione è continua in tutto l'intervallo di definizione.
Teoremi:
Se due o più funzioni sono continue in un intervallo anche la loro somma algebrica è una funzione
continua nell'intervallo. Lo stesso vale per il prodotto di due o più funzioni. Il rapporto di due
funzioni continue in un intervallo è una funzione continua nell'intervallo con l'eccezione di quei
valori per i quali si annulla il denominatore
Usando questi teoremi è facile dimostrare che:
1. La funzione costante è continua in ogni punto
2. Ogni funzione razionale intera è continua in R
3. Ogni funzione razionale fratta f(x)=A(x)/B(x) è continua per ogni valore che non annulli il
denominatore.
x
4. La funzione
y=a
5. La funzione
y=log a x
è continua per ogni valore di x
è continua per ogni valore positivo di x
Le funzioni più comuni hanno la seguente proprietà: gli intervalli di continuità coincidono con il
dominio ma non è sempre così.
Nell'esempio 2, infatti, troviamo una funzione il cui dominio è: D=[0,4] ma l'intervallo di continuità
è: [0,3)U(3,4].
Un altro esempio:
Studiare la continuità della seguente funzione
{
+4 se x⩾1
f ( x ) = −4x
2
x +1 se x<1
Questa funzione è una retta per ogni x maggiore o uguale a 1 ed è una parabola per ogni x minore di
1.
La funzione è sicuramente continua per x<1 (è una funzione polinomiale, parabola in questo caso)
ed è continua anche per x>1 (è una funzione polinomiale, retta in questo caso).
L'unico punto da studiare è x=1
1.
f (1)=0 si trova osservando che se x=1 dobbiamo considerare la retta e non la parabola
2. Il limite in questo caso non esiste: il limite destro è diverso dal limite sinistro. Infatti risulta:
lim f ( x)=0
lim f ( x)=2
-
x→ 1
x →1
+
N.B. Quando fai il limite destro devi “avvicinarti” partendo da valori più grandi di 1 e quindi devi
considerare la retta. Quando fai il limite sinistro devi “avvicinarti” da sinistra e quindi devi
page 4/5
considerare la parabola.
La funzione è quindi discontinua nel punto x=1 e, pertanto, gli intervalli di continuità sono:
(−∞ ,1 ) U (1 ,+∞ )
Abbiamo quindi stabilito gli intervalli di continuità senza disegnare il grafico.
Possiamo, comunque, verificare quanto detto disegnando il grafico della funzione:
Teoria da pag. 113 mod U
Esercizi : studia la continuità delle funzioni di pag. 198 e 199 mod U numeri: 642,644,648,649.
(Tralascia la classificazione dei punti di discontinuità)
page 5/5