Soluzione

UNIVERSITA’ DEGLI STUDI DI SASSARI
DIPARTIMENTO DI SCIENZE ECONOMICHE E AZIENDALI
MACROECONOMIA - Anno accademico 2015 - 2016, I ° semestre
Soluzioni esercitazione (prima parte del programma), 30.10.2015.
PARTE A)
1)
Effetto simile alla crescita demografica. Non si verifica un aumento dei lavoratori ma ogni lavoratore è
in grado di produrre una maggiore quantità di beni e servizi con il fattore “tempo-t” rimasto costante;
questo si traduce in un aumento del “numero effettivo” di lavoratori.
k = K/(L X E) = k per occupato effettivo;
y = Y/(L X E) = y aggregato per occupato effettivo = f(k) ;
Y/L = y X E = prodotto per occupato;
Y = y X (E X L) = prodotto totale;
Δ k = s f(k*) – (δ+n+g) k* = 0-zero
c* = f(k*) – (δ+n+g) k*
crescita di stato stazionario = 0;
crescita di stato stazionario = 0;
crescita di stato stazionario = g;
crescita di stato stazionario = n + g;
PMk = δ+n+g
Lt x Et = N°. L x efficienza L
2)
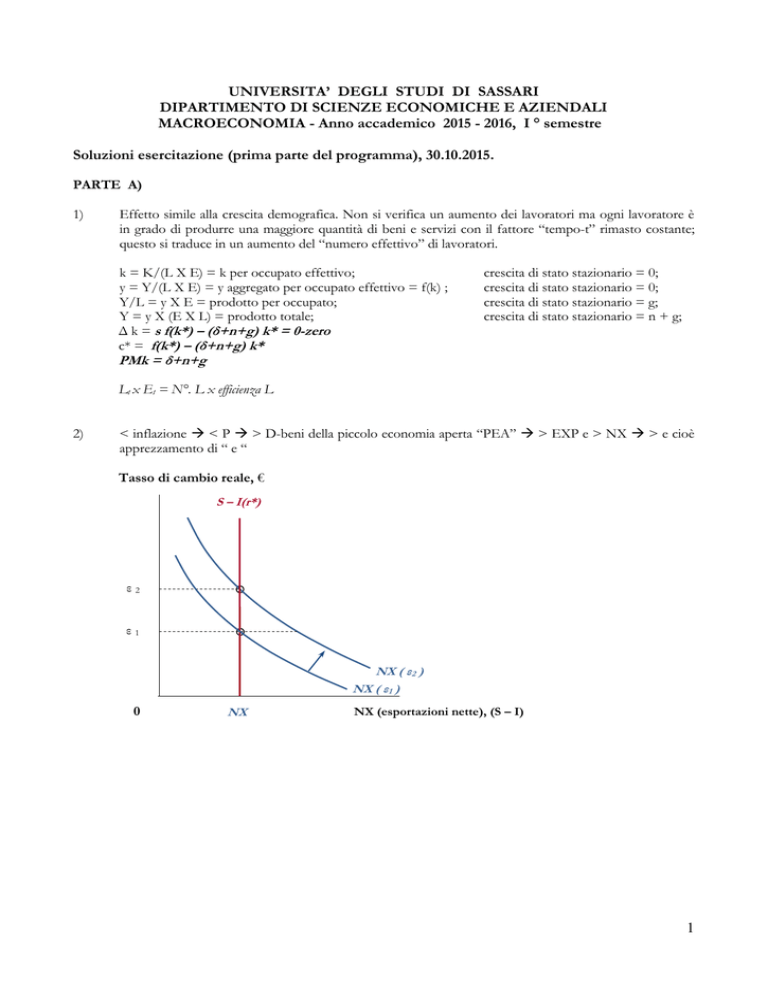
< inflazione  < P  > D-beni della piccolo economia aperta “PEA”  > EXP e > NX  > e cioè
apprezzamento di “ e “
Tasso di cambio reale, €
S – I(r*)
ε2
ε1
NX ( ε2 )
NX ( ε1 )
0
NX
NX (esportazioni nette), (S – I)
1
3)
S = I( r )
Tasso di interesse
S = OFM = offerta fondi mutuabili
S = insensibile ad “r”
r2
(OFM > DFM)  < r2
r*
r1
(OFM < DFM)  > r1
I (r) = DFM = domanda fondi mutuabili
0
S, I( r )
4)
Δ k = s f(k*) – (δ+n) k* = 0-zero
5)
> G  < SN  < [S – I ( r ) ]
Piccola economia aperta, tasso di cambio reale ed esportazioni nette.
Tasso di cambio reale, ε
S’’ – I(r*) S’ – I(r*)
ε2
ε1
NX ( ε )
0
NX ’’
NX ’
NX (esportazioni nette), (S – I)
2
6)
Y = C + I + G + NX;
da cui: Y – C – G = risparmio nazionale = S = I + NX; da cui:
S – I = NX;
S – I = deflusso di capitali;
NX = afflusso di capitali ;
Dunque : deflusso di capitali = afflusso di capitali
 avanzo bilancia dei pagamenti
 disavanzo bilancia dei pagamenti
(S – I ) ed NX entrambi > 0 (zero)
(S – I ) ed NX entrambi < 0 (zero)
Flusso di capitali (espressi da “S – I”) e flusso di beni e servizi (espressi da “NX” dato dalla differenza
fra le esportazioni e le importazioni) sono i due lati della “stessa medaglia”.
S>I
(S – I) > 0-zero 
S<I
(S – I) < 0-zero 
investimento nazionale netto estero ovvero prestiti italiani
all’estero
investimento estero netto in Italia ovvero prestiti dall’estero
S – I = NX  (OVALUTA = DVALUTA )
7)
MV = PQ = PIL ;
v = 1/k ;
k = costante;
(M/P)d = k Y = L ( i, Y)
b) Il PIL nominale dipende da “M”
8)
Il tasso di cambio nominale è il prezzo relativo delle valute di due paesi, cioè il prezzo di una valuta/moneta in
termini dell’altra. La contabilità economica nazionale ed internazionale precisa i seguenti due criteri considerando
nella definizione, sempre in primo luogo la valuta nazionale ed in secondo luogo la valuta estera (il termine ”X”
indica “per “ e/o “necessaria per ottenere”):
-
Criterio “certo X incerto”, cioè “certa” la quantità di valuta nazionale X “incerta” la quantità di valuta
estera;
esempio: 1 € (quantità nazionale certa, valore fisso) = 1,10 $/dollari USA (quantità di valuta estera
incerta, valore variabile in base all’andamento del mercato valutario);
-
Criterio “incerto X certo”, cioè “incerta” la quantità di valuta nazionale X “certa” la quantità di valuta
estera;
esempio: 0,909 € (quantità nazionale incerta, valore variabile in base all’andamento del mercato valutario)
= 1 $/dollari USA (quantità di valuta estera certa, valore fisso)
In Europa, con l’adozione della valuta euro, si è passati dal precedente criterio “incerto X certo”,
all’attuale “certo X incerto”, cioè il quantitativo di valuta domestica “euro”, per esprimere il valore
nominale del tasso di cambio, si considera sempre “certa” pari all’unità; l’inverso accade per i paesi
stranieri, come ad esempio gli USA il cui valore del tasso di cambio nominale si esprime nella formula
“incerto X certo”. (suggerimento: prima di procedere con le operazioni e rappresentazioni dei tassi di
cambio è preferibile definire il paese di residenza e la valuta presa in considerazione).
3
Rappresentazione.
Tasso di cambio flessibile U$A/euro (metodo incerto x certo, dal lato dei cittadini residenti negli USA).
Tc $/€
O- valuta estera = OVE
Tasso di cambio
di equilbrio =
Tc *.
D- valuta estera = DVE
0
Q*- €
Q – valuta estera - €
DVE : domanda valuta estera €, i cittadini USA desiderano acquistare prodotti/titoli europei, offrono $ contro €
sul mercato per pagare i prodotti/titoli europei in €, il $ si deprezza e l’ € si apprezza.
OVE : offerta di valuta estera €, i cittadini europei desiderano acquistare prodotti/titoli USA, offrono € contro $
sul mercato per pagare i prodotti/titoli USA in $, il $ si apprezza e l’ € si deprezza.
Quando il tasso di cambio flessibile U$A/euro, in scala grafica, sale da 1,00 a 1,50, cioè si passa da 1,00 $ a 1,5 $
per acquistare 1,00 €, significa che il $ si deprezza (ne serve una maggiore quantità per l’acquisto di €) e l’ € si
apprezza; questo evento stimola il desiderio dei cittadini europei, ad un cambio ad essi più favorevole, di
acquistare prodotti USA e pertanto offrono € sul mercato in cambio di $, dunque il deprezzamento del $ - il
prezzo del $ per 1,00 € - in definitiva, determina l’aumento del prezzo dell’ €, che a sua volta aumenta la quantità
offerta di € (legge di offerta). Crescono le esportazioni USA e si riducono quelle europee.
Quando il tasso di cambio flessibile U$A/euro, in scala grafica, scende da 1,50 a 1,00, cioè si passa da 1,50 $ a
1,00 $ per acquistare 1,00 €, significa che il $ si apprezza (ne serve una minore quantità per l’acquisto di €) e l’ € si
deprezza; questo evento stimola il desiderio dei cittadini USA, ad un cambio ad essi più favorevole, di acquistare
prodotti europei e pertanto offrono $ sul mercato in cambio di €, dunque l’ apprezzamento del $ - il prezzo del $
per 1,00 € -, in definitiva, determina la diminuisce il prezzo dell’ €, che a sua volta aumenta la quantità domandata
di € (legge di domanda). Diminuiscono le esportazioni USA e crescono quelle europee.
Il tasso di cambio reale tra due paesi è il prezzo relativo dei beni prodotti in quei due paesi. Vale a dire, il tasso
di cambio reale indica quale è il rapporto al quale i beni di un paese possono essere scambiati con quelli di un
altro paese. Talvolta ci si riferisce a tale rapporto di prezzi con l’espressione ragioni di scambio (le ragioni di
scambio sono date dal rapporto tra il livello dei prezzi dei beni esportati ed il livello dei prezzi dei beni importati,
espressi entrambi in una stessa valuta).
Per vedere la relazione che esiste fra tasso di cambio reale e tasso di cambio nominale si considera un bene che
molti paesi producono: le automobili. Si suppone che un automobile prodotta in Italia abbia un prezzo di
10.000,00 euro e che un’automobile simile prodotta in America abbia il prezzo di 20.000,00 dollari. Per
confrontare i prezzi delle due automobili si devono esprimere nella stessa valuta. Quando per acquistare un
dollaro occorre un euro, un’automobile italiana si acquista con 10.000,00 dollari.
Quindi, confrontando il prezzo dell’automobile prodotta in Italia con il prezzo dell’automobile prodotta in
America, si conclude che l’automobile italiana costa la metà di quella americana; in altre parole, ai prezzi correnti,
si possono scambiare due automobili italiane contro un’automobile americana.
4
Il tasso di cambio reale – il prezzo relativo dei beni prodotti in due paesi differenti – dipende dal tasso di cambio
nominale e dai prezzi dei beni nei due paesi espressi nelle rispettive valute. I calcoli sopra effettuati si possono
così riassumere:
Tasso di cambio
Reale
=
(1 euro/dollaro) x (10.000,00 euro/auto ITA)
(20.000,00 dollari/auto USA)
=
1
auto americana
2
auto italiana
=
A questi prezzi e a questo tasso di cambio nominale, con un’automobile americana si ottengono due automobili
italiane. Più in generale, la formula del tasso di cambio reale, con riferimento ad un generico bene prodotto nei
due paesi, è la seguente (criterio certo x incerto, vale a dire, come prevede la terminologia della contabilità
economica nazionale, “valuta nazionale certa X valuta estera incerta” ):
Tasso di cambio
Reale, Epsilon, ε
=
Tasso di cambio nominale x Prezzo del bene nazionale
Prezzo del bene estero
ε = e* x ( P / P* )
e* = ε x ( P* / P )
Tasso di cambio nominale = tasso di cambio reale x rapporto del livello prezzi ( P* / P )
P* = livello dei prezzi dei beni esteri (inflazione estera)
P = livello dei prezzi dei beni interni (inflazione interna)
ε = Epsilon = tasso di cambio reale
e* = tasso di cambio nominale
Il rapporto al quale un dato bene prodotto all’interno può essere scambiato con un bene simile prodotto
all’estero dipende dunque dai prezzi del bene nei due paesi espressi nelle rispettive valute e dal rapporto di
cambio tra le valute dei due paesi.
Il tasso di cambio reale tra due paesi è calcolato sulla base del tasso di cambio nominale e dei livelli dei prezzi nei
due paesi. In base alla suddetta definizione del tasso di cambio reale:
-
quando il valore del tasso di cambio reale è alto, i beni esteri sono relativamente a buon mercato ed i beni interni sono
relativamente cari e si riducono le esportazioni nette;
quando il valore del tasso di cambio reale è basso, i beni esteri sono relativamente cari ed i beni interni sono relativamente a
buon mercato ed aumentano le esportazioni nette.
Quando il livello dei prezzi interni “P” aumenta, il tasso di cambio nominale “ e* “ diminuirà; la moneta nazionale si è
deprezzata, ed occorrerà una maggiore quantità di moneta nazionale per acquistare una unità di valuta estera.
Quando il livello dei prezzi esteri “P* “ aumenta, il tasso di cambio nominale “ e* “ aumenterà; la moneta estera si è deprezzata,
ed occorrerà una minore quantità di moneta nazionale per acquistare una unità di valuta estera.
5
Tasso di cambio reale, 1/ε (certo x incerto)
Nell’asse “y” , in scala, si indica
“1/ε” per dimostrare - in base al
criterio “certo X incerto” - che man
mano che il tasso di cambio della
valuta “euro” si deprezza (e dunque
il
valore
“1/ε”
si
riduce
avvicinandosi all’origine), aumentano
le esportazioni dei paesi dell’area
euro.
NX ( ε )
0
NX (esportazioni nette) euro
NX = 0
Una parte dell’asse orizzontale del grafico indica valori negativi di “NX” (quando le importazioni sono maggiori
delle esportazioni, per valori a sinistra di “NX = 0-zero”).
ε = e* x ( P / P* )
> P  > ε e < NX
< P  < ε e > NX
9)
Agricoltore
Mulino
Panificio
0,20 x 100 kg
0,90 x 100 kg
1,50 x 120 kg
PIL = P Q = 1,50 x 120 kg = 10
VA = valore aggiunto
10)
= 20
= 90
= 180
VA 20
VA 70 cioè 90 - 20
VA 90 cioè 180 – 90
totale
VA 90 + 70 + 20 = 180
Piccola economia aperta, tasso di cambio reale ed esportazioni nette.
Ipotesi di perfetta mobilità di capitali e tasso di interesse interno uguale a quello internazionale.
< DINTERNA  < I  > (S – I) cioè (S – I) v/destra
6
Tasso di cambio reale, ε
S’ – I’(r*) S’ – I’’(r*)
ε1
ε2
NX ( ε )
0
NX ’
NX ’’
NX (esportazioni nette), (S – I)
7
PARTE B)
Soluzione esercizio 1.
Y = C + I + G + NX
Y = 5500;
G = 1500;
T = 1500;
r = 5;
NX = 500 – 500 ε
C = 250 + 0,75 (Y – T);
I = 1000 – 50 r
a)
S=Y–C–G
S = 5500 – 250 - 0,75 (5500 – 1500 ) – 1500 = 5250 – 3000 – 1500 = 750
I = 1000 – 50 5 = 750
NX = S – I = 750 – 750 = 0
0 = 500 - 500 ε = 500 – 500 x 1 = 0;
ε=1
b)
G = 2000
S=Y–C–G
S = 5500 – 250 - 0,75 (5500 – 1500 ) – 2000 = 5250 – 3000 – 2000 = 250
I = 1000 – 50 5 = 750
NX = S – I = 250 – 750 = - 500
- 500 = 500 - 500 ε = 500 – 500 x 2 = - 500; ε = 2
c)
r = 10
S=Y–C–G
S = 5500 – 250 - 0,75 (5500 – 1500 ) – 1500 = 5250 – 3000 – 1500 = 750
I = 1000 – 50 10 = 500
NX = S – I = 750 – 500 = 250
250 = 500 - 500 ε = 500 – 500 x 0,5 = 250;
ε = 0,5
8
Soluzione esercizio 4 parte B).
Crescita economica di lungo periodo; stato stazionario di regola aurea (modello del Prof. Robert Solow,
N.E. 1987).
Y = f (K, L)
OFFERTA DI BENI
zY = f (zK, zL)
ipotesi di rendimenti di scala costanti: moltiplicando i fattori per una costante “z”
(positiva) il prodotto cresce della stessa proporzione “z”.
Y/L = f (K/L, L/L)
la funzione con rendimenti di scala costanti consente di analizzare tutte le variabili del
sistema economico in relazione alla grandezza della forza lavoro “L”; si pone “ z = 1/L
Il prodotto per occupato “Y/L” è funzione del capitale per occupato “K/L”, in quanto
“L/L” che è uguale ad “1” può essere del tutto tralasciato in quanto “costante”.
Le dimensioni dell’economia sono misurate dal numero dei lavoratori e “non
influenzano” il rapporto prodotto per occupato “Y/L” e capitale per occupato “K/L”;
per questo motivo si esprimono tutte le variabili “non in riferimento all’economia”,
bensì “per singolo occupato” e la simbologia delle lettere alfabetiche indicate “in
minuscolo” rispecchia questa impostazione
y = f(k)
y = f(k)
= funzione di produzione con pendenza positiva decrescente ad indicare la crescita con
andamento del PMK (prodotto marginale del capitale) decrescente
(a) prodotto totale del “k” per occupato
PTk
(b) prodotto marginale del “k”
PM
PTk
40
40
35
30
30
20
20
10
10
0
1
2
3
4
5
k per occupato
0
PMk
1
2
3
4
5
k-occ.
Il prodotto marginale deriva dal prodotto totale.
Nel diagramma a) è rappresentata la curva del prodotto totale del capitale “k” per occupato che sale/aumenta in maniera
decrescente quando vengono aggiunti nuovi input di capitale e mantenendo costanti gli tutti altri elementi (altri fattori
produttivi, tecnologia e altri elementi esogeni); ogni punto della suddetta curva rappresenta il prodotto marginale del capitale
ed unendo i punti si ottiene la curva in “colore marrone” (prodotto totale). Questo modello di economia è di tipo “classico”
Il diagramma b) mostra i gradini decrescenti del prodotto marginale del capitale. Ogni rettangolo in “colore grigio” indicato
in b) è uguale al corrispondente rettangolo indicato in a). La zona in b) sotto la curva in “colore rosso” del prodotto
marginale del capitale (o somma dei rettangoli) indica il relativo prodotto totale del capitale riportato nei rettangoli in “colore
grigio” della zona di a).
PMK = f( k + 1) - f(k)
9
Y = f (K, L) = y = f(k)
OFFERTA DI BENI = y
(OFFERTA DI BENI = y = DOMANDA DI BENI = c + i)  EQUILIBRIO DEL SISTEMA
y = c + i (+ G + NX)
“G” tralasciata ed “NX” non presente poiché trattasi di economia chiusa
s = s/costante = f(y)
0 < s < 1; s = propensione marginale al risparmio; “s” è funzione del reddito
c = ( 1 – s )y
propensione marginale al consumo; 0 < c < 1; “c” è funzione del reddito
y = c + i = ( 1 – s )y + i
si sostituisce il valore di “c” nella funzione di produzione esprimendolo in
termini di risparmio, stabilendo così la relazione fra risparmio “s” ed “y” ;
influenzando il risparmio “s” (ed i consumi) si condiziona indirettamente “y”
y = c + i = y – sy + i
riordinando i termini ed esprimendo l’equazione rispetto ad “i” si ha:
sy = i ; oppure i = sy
il risparmio, che è in funzione del reddito, è uguale all’investimento, come
dimostrato a livello aggregato con l’eguaglianza “ S = I “
per ogni dato stock di capitale “k” la funzione di produzione “ y = f(k) “
determina la produzione aggregata del sistema economico ed il saggio di
risparmio “s” stabilisce la ripartizione della stessa produzione “y” fra consumo
“c” ed investimento “i”
i = s f(k)
si sostituisce ad “y” la corrispondente funzione di produzione che a sua volta è
pari alla funzione di capitale “k” per occupato; lo stock di capitale esistente “k”
è in funzione dell’accumulazione di nuovo capitale attraverso “i”; il prodotto
“y” è determinato dalla funzione di produzione “f(k)” e la ripartizione della
stessa produzione “y” fra consumo “c” ed investimento “i” dipende dal saggio
di risparmio “s”
Δ k = i – δ k = s f(k) - δ k
“Δ k” è la variazione del capitale nel tempo per effetto del suo aumento
all’aumentare di “i” che origina il “PMk” (prodotto marginale del capitale via
via decrescente) e per effetto della sua riduzione a seguito del suo
deperimento/ammortamento indicato da “δ k (via via crescente)“; si raggiunge
l’ottimo, secondo il modello “classico”, spingendo la produzione fino a quando
il “PMk (decrescente) = δ k (crescente)” e cioè fino a quando;
Δ k* = s f(k*) - δ k* = 0-zero k* - stazionario e quando massimizza il massimo livello di consumo è chiamato
livello di capitale k*GOLD di lungo periodo di regola aurea; in stato stazionario
l’ammortamento compensa interamente ed esattamente l’investimento; dal
capitale k*GOLD di lungo periodo di regola aurea si determina il consumo
c*GOLD di lungo periodo di regola aurea mediante semplici sostituzioni nelle
equazioni suindicate
y=c+i
c = y - i = f(k*) – i
c = f(k*) – δ k*
stato stazionario ottimo quando “ PMk = i = δ k “
Δ k = s f(k*) – (δ+n+g) k* = 0-zero
con popolazione “n” e tecnologia ”g”
“PMk - δ“ > 0 
> c*GOLD finale , k < k*GOLD,
“> i con > s” e “< c “ nell’immediato
“PMk - δ“ < 0 
< c*GOLD finale , k > k*GOLD,
“< i con < s” e “> c “ nell’immediato
10
(a)
(b)
Unico saggio di risparmio e regola aurea.
Y, C, I
Y(prodotto) , Ammortamento, Investimento
δ k*
f(k*)
prodotto, y
α = pendenza
consumo,
consumo,
c c
C* gold
s (risparmio) gold f (k*)
i* gold
α
α
0
investimento, i
0
t0
Tempo
k* gold
k - per occupato
Δs
spostamento curva s f (k*) e < C (consumo).
k* gold = capitale per occupato di stato stazionario
Un aumento del saggio di risparmio - da parte dello stato - al tempo “ t0 ” quando lo stock di capitale
nell’economia è inferiore al livello di regola aurea; l’aumento del saggio di risparmio, al tempo “ t0 ” , determina
una immediata riduzione del consumo iniziale ed una contemporanea espansione dell’investimento; con il tempo
che passa da “ t0 ” a “ t1 ”, “ t2 ”, “ tn ” l’investimento genera l’aumento del prodotto e del consumo ed al nuovo
stato stazionario, il nuovo consumo finale è maggiore di quello iniziale.
Stato stazionario: “pendenza funzione di produzione = pendenza funzione di ammortamento”, cioè “PMk*” =
δ“ . Il saggio di risparmio condiziona il livello di stato stazionario.
Gli organi di politica economica degli stati dovrebbero adottare i provvedimenti per raggiungere il livello di
capitale di regola aurea.
Perché nel modello si utilizza il termine “regola aurea ”?
R.M.Solow ed i suoi collaboratori, hanno costruito un modello di crescita economica individuando, sulla base del
modello classico dell’economia, un livello di accumulazione di capitale ottimale che assicuri un giusto equilibrio
delle risorse (capitale, investimenti, risparmi, determinazione dei consumi ottimali) fra le generazioni presenti e
future con l’attribuzione degli stessi pesi; la denominazione di “stock di capitale al livello di stato stazionario di
regola aurea”, deriva dalla regola aurea della Bibbia (N.T., S.Mt. cap.7, v. 12-13 : “ Tutto quanto volete gli uomini
facciano a voi, anche voi fatelo a loro; …”).
11
Soluzione parte B) esercizio 4.
a)
Funzione di produzione per occupato?
α
Yt = AKt Lt
1- α
divido per Lt ,
α
Yt / Lt = (AKt/ Lt ) (Lt / Lt )
yt = A kt
b)
1- α
pongo (“Yt/ Lt )” = yt , e (“Kt/ Lt )” = kt ;
(Lt / Lt )
1- α
=1
α
i) k* ? ii) reddito pro-capite stato stazionario ? iii) tasso di crescita di K pro-capite in transizione stato
stazionario ?
Δ k = s f(k*) – (δ+n) k* = 0-zero
i)
(δ+n) k* = s f(k*)
(δ+n) k* = s A k*
poichè “ f(k*) = y* = A k*
α
α
(1 – α)
= (s A)/(δ+n)
k* = [(s A)/(δ+n)]
α
poichè (k*/ k* )= k*
y* = A k*
iii)
Δ kt = s f(kt) – (δ+n) kt
α
(1 – α)
, (nota *) sostituendo si ha :
1/(1 – α)
ii)
Δ kt = s A kt
“ , come da precedente quesito a), si ha:
dividendo le potenze di entrambi i membri per “ 1 – α “, si ricava:
(nota *): esempio numerico: 2/2 2 =2/4 = 1/2;
α
α
riordinando i termini si ha:
(k*/ k* ) = [s A/(δ+n)]
k*
da cui, riordinando i termini
vedi a) yt = A k*t
– (δ+n) kt
2/2 2 = 2 1 – 2 = 2 – 1 = 1/2 1 = 1/2
α
poichè “f(kt) = yt “ e “ yt = A kt
α
“Δ kt > 0-zero” nel caso di K < K* ;
“Δ kt < 0-zero” nel caso di K > K*
c)
quando “ k < k*GOLD “  servono > “ i “ per arrivare a “ > c*GOLD” ; quindi salgono i “ c*GOLD”;
quando “ k < k*GOLD “ ,
[s f(k) - (δ+n) k] > 0
cioè
s f(k) > (δ+n) k
dunque è necessario aumentare “s” per aumentare “ i “.
Sono gradite le segnalazioni di eventuali errori e/o integrazioni; agli studenti, tutti, auguro buon lavoro, G.B.Becugna.
Ricevimento studenti: nelle date ed orari indicati sul sito www.macroeconomia.uniss, c/o DiSea, Sassari, Via Torre Tonda
n. 34. Resto disponibile per quanto possa servire ([email protected]).
12