Gruppo N° 3
(1) Il candidato risolva il seguente esercizio, illustrando con chiarezza, rigore e sintesi i procedimenti
utilizzati.
Erone di Alessandria, nel primo secolo d.C., ha scoperto la formula
√
Area triangolo = s(s − a)(s − b)(s − c) ,
(dove s è il semiperimetro e a, b, c sono le lunghezze dei lati del triangolo opposti, rispettivamente,
ai vertici A, B, C), studiando le proprietà dei cerchi che sono tangenti simultaneamente ai tre lati del
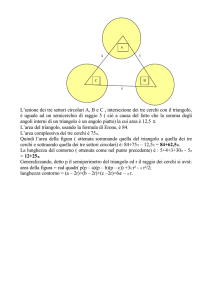
triangolo, o ai loro prolungamenti. Due di tali cerchi sono tracciati nel disegno in figura 1:
- il cerchio inscritto di centro I e raggio r, che è tangente ai tre lati del triangolo ABC nei punti
A′ , B′ , C′ .
- il cerchio esterno di centro E e raggio R, che è tangente al lato AB del triangolo, e alle rette
ottenute prolungando i lati AC e BC, rispettivamente nei punti W , V , U.
Studiando la figura 1, si chiede al candidato di ripercorrere i passi del ragionamento di Erone, dimostrando che:
1) i segmenti di tangente tracciati dai vertici A, B, e C al cerchio inscritto hanno lunghezze
AB′ = AC′ = s − a
BA′ = BC′ = s − b
CA′ = CB′ = s − c ;
2) i segmenti di tangente al cerchio esterno hanno lunghezze
CU = CV = s
BU = BW = s − a
AV = AW = s − b .
3) Si chiede quindi di utilizzare la similitudine di opportune coppie di triangoli, scelti tra quelli
formati dai centri I ed E con i vertici del triangolo e con i punti di tangenza, per dimostrare che
i raggi r e R dei cerchi tangenti sono definiti dalle proporzioni
R : r = s : (s − c)
r : (s − a) = (s − b) : R ,
da cui discende l’espressione
r2 =
(s − a)(s − b)(s − c)
s
per il raggio del cerchio inscritto.
4) Infine si chiede di dimostrare la formula
1
Area triangolo = r(a + b + c) = rs
2
e di dedurre da essa la formula di Erone.
(2) Scrivere le equazioni di Maxwell e discuterne significato fisico e conseguenze.
C
Ĉ
2
(s −
c)
Ĉ
2
B′
r
a)
A′
(s −
I
Â
2
Â
2
C′
W
B
(s −
b)
A
V
R
U
E
F 1. La notazione
Â
2
indica la metà dell’angolo in A del triangolo ABC.