5
A
4
3
C
B
5
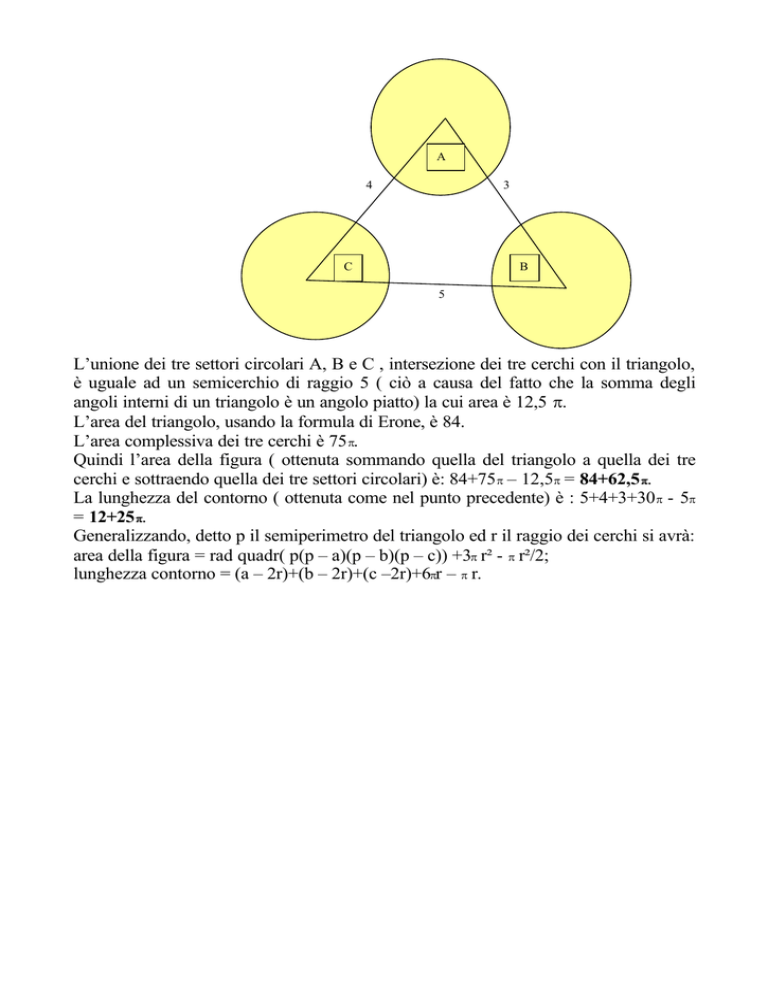
L’unione dei tre settori circolari A, B e C , intersezione dei tre cerchi con il triangolo,
è uguale ad un semicerchio di raggio 5 ( ciò a causa del fatto che la somma degli
angoli interni di un triangolo è un angolo piatto) la cui area è 12,5 π.
L’area del triangolo, usando la formula di Erone, è 84.
L’area complessiva dei tre cerchi è 75 π.
Quindi l’area della figura ( ottenuta sommando quella del triangolo a quella dei tre
cerchi e sottraendo quella dei tre settori circolari) è: 84+75 π – 12,5π = 84+62,5 π.
La lunghezza del contorno ( ottenuta come nel punto precedente) è : 5+4+3+30 π - 5π
= 12+25 π.
Generalizzando, detto p il semiperimetro del triangolo ed r il raggio dei cerchi si avrà:
area della figura = rad quadr( p(p – a)(p – b)(p – c)) +3π r² - π r²/2;
lunghezza contorno = (a – 2r)+(b – 2r)+(c –2r)+6πr – π r.












