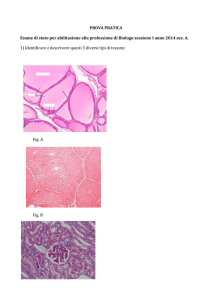
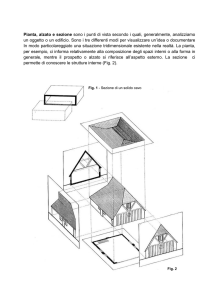
1
GEOMETRIA EUCLIDEA
GEE
1. L'assioma della parallela.
Il sistema { A1, … , A7 } definisce la geometria metrica assoluta del piano Π.
Introduciamo ancora un assioma.
A8
Assioma della parallela
Data una retta r e un punto P ∉ r, esiste una e una sola retta passante per P parallela a r.
Il sistema { A1, … , A8 } definisce la geometria euclidea del piano Π. Da qui deriva, il nome di piano eucli
deo che comunemente si dà all'insieme Π. Vediamo subito una prima importante conseguenza dell'A8.
La relazione di parallelismo in
è una relazione di equivalenza.
Dobbiamo provare che, per ogni r, s, t ∈ :
Dim.
a
r // r
b
r // s
c
( r // s ∧ s // t )
(proprietà riflessiva)
s // r
(proprietà simmetrica)
r // t
(proprietà transitiva)
− Le proprietà a e b sono contenute nella definizione stessa di parallelismo.
− Per assurdo, se r e t fossero incidenti, per il loro punto d'intersezione P passerebbero due
rette parallele a s. Questo, per l'A8, non può verificarsi. Quindi c.
La relazione di parallelismo in
determina allora una partizione di
dice una direzione. Una retta qualsiasi r ∈
direzione di tutte le sue parallele.
in classi di equivalenza. Ogni classe si
individua così una direzione [r], che è la sua direzione, ed è la
2. Il rapporto di proiezione
DEF
Dato un insieme piano ℑ e una retta x, si chiama proiezione ortogonale di ℑ su x, l'applicazione
prx: ℑ → x che ad ogni punto P ∈ ℑ fa corrispondere il punto P'∈ x a distanza minima da P.
Il punto P' a distanza minima da P è il punto d'intersezione della perpendicolare alla retta x condotta per P
(fig.1). Il punto P' = prx(P) si dice proiezione ortogonale di P su x.
ℑ
r
P
(fig.1)
(fig.2)
P
x
x
P'
P'
In particolare, se l'insieme che si proietta è una retta r non perpendicolare a x, allora prx è un'applicazione
bijettiva di r in x (fig.2); se invece r ⊥ x, allora prx è un'applicazione costante.
Le seguenti definizioni ci saranno utili in seguito. Consideriamo un angolo
colare in O al lato
inclusa nel semipiano di origine
Ô e sia y la semiretta perpendi
che include n. Ora, se n = y, l'angolo Ô è, come sap
piamo, retto (fig.3); se il lato n è interno all'angolo Ôy, l'angolo Ô si dice acuto (fig.4); infine, se il lato
esterno all'angolo Ôy, l'angolo Ô si dice ottuso (fig.5).
è
2
y
y
n =y
n
O
n
O
Ô
è retto (fig.3)
O
è acuto (fig.4)
Ô
Ô
è ottuso (fig.5)
Ciò premesso, vale la seguente importantissima proposizione che, per brevità, ci limitiamo ad enunciare.
Sia Ô un angolo acuto. Per ogni P∈ n, se P' = pr (P) , allora esiste uno e un solo
numero reale k ≥ 0 tale che:
OP ′ = k ⋅ OP
(1)
Il numero reale k prende il nome di rapporto di proiezione di n su
O
punto di n che si proietta:
=
(fig.6). Tuttavia, se immaginiamo di variare il lato
Di più, il teorema vale anche quando n ⊥
OQ′
OQ
P
n
.
La chiave di questo teorema è che k è costante, cioè non dipende dal
OP′
OP
Q
P'
Q'
= ... = k .
(fig.6)
n tenendo fisso il vertice O, varierà anche k.
o n = . Nel primo caso, ogni punto di n si proietta in O e la (1) va
le per k = 0; nel secondo, ogni punto di n si proietta su se stesso e la (1) vale per k = 1. In tutti gli altri casi,
essendo OP ′ < OP , risulta k < 1. Quindi k ∈ [ 0, 1 ].
Infine, si dimostra che il rapporto di proiezione di n su
è uguale al rapporto di proiezione di
su n .
Sul rapporto di proiezione si basa una delle numerose dimostrazioni del famoso teorema di Pitagora.
Prima di enunciarlo, ricordiamo che si chiama triangolo rettangolo ogni triangolo che ha un angolo retto.
I lati adiacenti all'angolo retto si dicono cateti, il lato opposto si dice ipotenusa. Gli angoli adiacenti all'ipote
nusa sono angoli acuti.
In un triangolo rettangolo, il quadrato della lunghezza dell'ipotenusa è uguale alla somma dei
quadrati delle lunghezze dei cateti.
Dim.
Il triangolo ABC abbia l'angolo retto in A e sia H la proiezione ortogonale di A sulla semiret
ta BC (qui con la notazione BC indichiamo la semiretta di origine B passante per C).
A
A
(fig.7)
(fig.8)
B
H
C
B
H
C
Sia k il rapporto di proiezione della semiretta BC sulla semiretta BA (fig.7).
Se proiettiamo il punto C sulla semiretta BA, si ottiene:
BA = k ⋅ BC .
Se proiettiamo il punto A sulla semiretta BC, si ottiene:
BH = k ⋅ BA
(1)
(2)
e, sostituendo nella (2) il valore di BA dato dalla (1), si deduce:
BH = k2 ⋅ BC .
(3)
3
Sia k' il rapporto di proiezione della semiretta CB sulla semiretta CA (fig.8).
Se proiettiamo il punto B sulla semiretta CA, si ottiene:
(4)
CA = k' ⋅ CB .
Se proiettiamo il punto A sulla semiretta CB, si ottiene:
(5)
CH = k' ⋅ CA
e, sostituendo nella (5) il valore di CA dato dalla (4), si deduce:
CH = k'2 ⋅ CB .
(6)
Poiché H appartiene alla semiretta BC e anche alla semiretta CB, H sta fra B e C. Allora:
(7)
BC = BH + CH
e, sostituendo nella (7) i valori di BH e di CH dati dalla (3) e dalla (6), si deduce:
BC = k2 ⋅ BC + k'2 ⋅ BC .
(8)
Da questa, moltiplicando membro a membro per BC , si ricava:
BC 2 = k2 ⋅ BC 2 + k'2 ⋅ BC 2
(9)
e, tenendo conto della (1) e della (4), si ottiene:
BC 2 = BA 2 + CA 2
che è la tesi del teorema di Pitagora.
Notiamo che dalla (8), dividendo ambo i membri per BC , si ottiene l'interessante relazione che lega i due rap
porti di proiezione: k2 + k'2 = 1.
3. Gli assi cartesiani
Fissato nel piano Π un punto O, siano X e Y due rette qualsiasi incidenti in O e fra loro ortogonali.
Ad ogni P ∈ Π possiamo far corrispondere i punti P' = prX(P) e P" = prY(P). Viceversa, data una coppia di
punti, P' ∈ X e P"∈ Y, esiste uno ed un solo punto P tale che prX(P) = P' e prY(P) = P" (fig.9).
Y
(fig.9)
P"
•
O
P
P'
X
Assegnato un verso su X e un verso su Y, per l'A5 risulta fissato, tanto su X quanto su Y, un sistema di coor
dinate di origine O. Allora indicata con x la coordinata di P' su X e con y la coordinata di P" su Y, risulta an
che definita un'applicazione bijettiva:
Φ : P∈Π
(x, y) ∈ IR2.
I numeri reali x e y si dicono le coordinate di P. In particolare, x si dice ascissa e y ordinata.
Per indicare che il punto P ha ascissa x e ordinata y, scriveremo P(x, y).
L'applicazione Φ prende il nome di riferimento cartesiano ortogonale OXY. Il punto O è chiamato origine
del riferimento; le rette X e Y si dicono assi cartesiani.
In fig.9 possono essere facilmente individuati alcuni sottoinsiemi notevoli di Π.
4
P(x, y) appartiene al …
se (x, y) appartiene a …
primo quadrante
IR+× IR+
secondo quadrante
IR−× IR+
terzo quadrante
IR−× IR−
quarto quadrante
IR+× IR−
semipiano delle ordinate positive
IR × IR+
semipiano delle ordinate non negative
semipiano delle ordinate negative
IR × IR 0+
IR × IR−
asse delle ascisse
IR × {0}
asse delle ordinate
{0} × IR
Il punto O (origine degli assi) ha coordinate (0,0).
4. Distanza fra due punti
Fissato nel piano Π un riferimento cartesiano ortogonale OXY, consideriamo i punti P(x1,y1) e Q(x2,y2).
Y
y1 = y2
O
Y
(fig.10)
P
x1
Q
x2
y2
Q
y2
y1
P
y1
O
X
Y
(fig.11)
x1 = x2
X
O
(fig.12)
Q
P
R
x1
x2
X
Se y1 = y2 (fig.10), P e Q si trovano su una retta parallela all'asse X; se invece x1 = x2 (fig.11), tali punti si
trovano su una retta parallela all'asse Y. Nel primo caso è PQ = x2 − x1; nel secondo PQ = y2 − y1.
Se y1 ≠ y2 e x1 ≠ x2 (fig.12), costruiamo il triangolo rettangolo RQP, con il cateto [PR] parallelo all'asse X e il
cateto [RQ] parallelo all'asse Y. Per il teorema di Pitagora, si ha:
2
da cui, essendo:
2
si deduce:
2
PQ = PR + RQ
PR = (x2 – x1)
PQ =
2
2
2
, RQ = (y2 – y1)2
(x 2 − x1 )2 + ( y 2 − y1 )2
(1)
La distanza dall'origine O di un punto P(x, y), ancora per il teorema di Pitagora, è data da:
OP =
x2 + y2
(2)
Se P ha coordinate (x, 0), cioè se P ∈ X, dalla (2) segue subito:
OP =
x 2 = x.
(3)
Infine, se P ha coordinate (0, y), cioè se P ∈ Y, risulta OP = y.
La (1), che esprime la distanza fra due punti mediante le coordinate, è di grande interesse. Essa permette
intanto di descrivere in termini algebrici la circonferenza.
5
Y
Assegnata una circonferenza T di centro C ( h, k ) e raggio r
( fig. 13 ), vogliamo determinare una equazione che risulti sod
disfatta dalle coordinate di tutti e solo i punti di T .
A tale scopo osserviamo che un punto P(x, y) appartiene a T se
e solo se la distanza di C da P è uguale a r. Facendo interveni
T
2
PC = (x – h) + (y – k)
•
P(x, y)
re, per semplicità, il quadrato della distanza, per la (1) si ha:
2
C
k
h
O
2
X
(fig.13)
2
da cui, essendo PC = r 2 , si deduce:
2
2
(x – h) + (y – k) = r 2
(4)
chiamata equazione cartesiana della circonferenza T.
Come si vede, abbiamo operato una specie di traduzione da un linguaggio ad un altro: dal linguaggio della
geometria al linguaggio dell'algebra.
5. Simmetrie nel piano cartesiano
Con l'espressione piano cartesiano intendiamo, da ora in poi, lo stesso piano euclideo sul quale sia stato fis
sato un riferimento cartesiano ortogonale OXY.
In questo paragrafo, vediamo come sia possibile "trasferire" al piano cartesiano alcune semplici isometrie.
Fissiamo, dunque, in Π un riferimento cartesiano ortogonale OXY.
Dato un punto P(x, y), vogliamo determinare le coordinate (x', y') del punto P' simmetrico di P rispetto
all'asse Y.
In primo luogo, è chiaro che l'ordinata non cambia, y' = y, perché P e P' si trovano sulla stessa perpendico
lare all'asse Y (fig.14). Per determinare l'ascissa di P', proiettiamo P e P' sull'asse X ottenendo i punti di ascis
sa x e x' rispettivamente. Trattandosi di un'isometria, deve essere x' =x, poiché detti punti hanno la stes
sa distanza dall'origine O. Di più, essi si trovano su semirette opposte rispetto ad O; quindi le loro ascisse
hanno segni opposti: x' = −x. Le uguaglianze x' = −x e y' = y si dicono le equazioni (cartesiane) di y.
∴
È
y
:
x′ = − x
y′ =
y
ovvero
y
x′
y′
:
−1 0
=
0
1
x
⋅
y
.
(1)
Dato un punto P(x, y), vogliamo determinare le coordinate (x', y') del punto P' simmetrico di P rispetto
all'asse X.
In questo caso (fig.15), le ascisse dei punti P e P' sono uguali, mentre le ordinate sono opposte.
Allora, le equazioni di X sono x' = x e y' = −y.
∴
È
X
:
x′ =
x
y′ = − y
ovvero
X
:
x′
y′
=
1
0
0 −1
⋅
x
y
.
(2)
Y
P'
x'
P
O
(fig.14)
x
P
y
X
x'
X
y'
P'
(fig.15)
P
y
P'
O
y'
(fig.16)
x
X
6
Dato un punto P(x, y), vogliamo determinare le coordinate (x', y') del punto P' simmetrico di P rispetto
all'origine degli assi.
Si tratta di determinare le equazioni della simmetria centrale di centro O (fig.16).
Sappiamo che
O
X.
Y
O:
x′
y′
=
Allora, come subito si riconosce, si ha:
1
0
∴
È
−1 0
⋅
0 −1
O
0
⋅
1
x
y
x′ = − x
y′ = − y
:
=
1
0
0 −1
ovvero
O
−1 0
⋅
⋅
1 1
x′
y′
:
x
y
−1 0
x
⋅
0 −1
y
=
−1 0
x
⋅
0 −1
y
=
.
.
(3)
Dato un punto P(x, y), vogliamo determinare le coordinate (x', y') del punto P' simmetrico di P rispetto
a una retta r //Y.
Una retta r parallela all'asse Y è il luogo di tutti e solo i punti che hanno la stessa ascissa h, ∀h ∈ IR:
r=
{ P(x, y) / x = h, ∀h ∈ IR }.
L'uguaglianza x = h si dice equazione (cartesiana) della retta r. Per indicare che la retta r ha equazione
x = h, scriviamo, brevemente, r : x = h.
Risulta y' = y, perché P e P' si trovano sulla stessa perpendicolare all'asse Y (fig.17).
Siano P1 = prX(P), P'1 = prX(P') e sia H il punto di coordinate (h, 0) in cui la retta r taglia l'asse X. Si ha subito
P1H = P1′H . Ma P1H =x − h, P1′H = x' − h. Ne segue che i numeri x − h e x' − h, avendo lo stesso valore
assoluto, o sono uguali o sono opposti fra loro. Il primo caso si realizza solo se x' = x; ma allora P coincide
rebbe con P' ed entrambi dovrebbero appartenere all'asse r. Nel secondo caso, quello che qui ci interessa, si
ha x – h = −(x' − h), da cui si ricava x' = −x + 2h.
∴
Y
r
P'
È
r
:
x′ = − x + 2h
y′ = y
ovvero
r
x′
y′
:
− 1 0 2h
=
1
0
⋅ y
0
0
1
1
Y
P
r
(fig.17)
s
P'
O
X
P1
P
M
P'
P'1
(4)
K
s
O
.
1
Y
P
x
0
O
X
X
H
(fig.18)
(fig.19)
Dato un punto P(x, y), vogliamo determinare le coordinate (x', y') del punto P' simmetrico di P rispetto
a una retta s //X.
Una retta s parallela all'asse X è il luogo di tutti e solo i punti che hanno la stessa ordinata k, ∀k ∈ IR:
s=
{ P(x, y) / y = k, ∀k ∈ IR }.
L'uguaglianza y = k è, allora, l'equazione della retta s, indicata scrivendo s : y = k.
Ora (fig.18), le ascisse dei punti P e P' sono uguali, x' = x. Quanto alle ordinate, con qualche passaggio si
trova y' = −y + 2k.
∴
È
s :
x′ = x
y′ = − y + 2k
ovvero
s :
x′
y′
1
1
=
0
0
x
0 − 1 2k ⋅ y
0 0
1
1
.
(5)
7
Dato un punto P(x, y), vogliamo determinare le coordinate (x', y') del punto P' simmetrico di P rispetto
a un punto M(h, k).
Sappiamo che
M
è la composta di due simmetrie assiali, con assi ortogonali r e s, che s'incontrano nel cen
tro M(h, k). Poiché la scelta delle rette r e s è arbitraria, possiamo prendere r : x = h e s : y = k (fig.19).
Da
M
=
s
M
:
r,
x′
y′
si ricavano le equazioni di
1
=
1
0
0
0
1
∴
Dalle equazioni di
− 1 0 2h
0
0 − 1 2k ⋅
M
È
M
0
1
M:
x
⋅ y
1
1
=
0
0
1
0
:
x′ = − x + 2h
y′ = − y + 2k
0
− 1 0 2h
0
0 − 1 2k ⋅
0 0
1
ovvero
M
:
0
0
1
0
x′
y′
=
1
0
1
−1
0
0
−1
x
⋅ y
1
0
=
0
0
0
2h
2h
x
− 1 2k ⋅ y
0
1
.
1
x
− 1 2k ⋅ y
0
1
1
.
(6)
si può dedurre un risultato molto utile. Infatti, ricavando h dalla prima e k dalla secon
da, con qualche passaggio, si ottiene:
h =
k =
x + x′
2
y + y′
2
(7)
che esprime le coordinate del centro di simmetria M in funzione delle coordinate di P e P'. La prima dice che
l'ascissa di M è la media aritmetica delle ascisse di P e P'; la seconda dice la stessa cosa per le ordinate.
Ma il centro di simmetria che scambia P con P' è il punto medio del segmento [PP']. Allora, le coordinate del
punto medio di [PP'] sono le medie aritmetiche delle coordinate omonime di P e P'.
6. Parallelogrammi
Due segmenti si dicono consecutivi, se hanno un solo estremo in comune; si dicono adiacenti, se sono
consecutivi e giacciono su una stessa retta.
DEF
L'unione di n ≥ 3 segmenti consecutivi e non adiacenti, si dice una poligonale.
Poligonale chiusa o poligono
Poligonale aperta
Poligonale intrecciata
(fig.20)
(fig.21)
(fig.22)
I segmenti che formano una poligonale si dicono lati della poligonale, i loro estremi vertici. Il primo estremo
del primo segmento e il secondo estremo dell'ultimo, si chiamano estremi della poligonale. Se gli estremi
coincidono, la poligonale si dice chiusa (fig.20), altrimenti aperta (fig.21). Una poligonale chiusa si dice, anche,
un poligono. Se due lati non consecutivi hanno un punto in comune, la poligonale si dice intrecciata (fig.22).
Un poligono con quattro lati si chiama quadrilatero. Il segmento che congiunge due vertici qualsiasi non con
secutivi di un quadrilatero non intrecciato si dice diagonale del quadrilatero.
Il nostro interesse prevalente è rivolto agli insiemi piani che hanno un asse di simmetria ( cioè che sono tras
formati in sé da una simmetria assiale ) oppure che hanno un centro di simmetria (cioè che sono trasformati
in sé da una simmetria centrale ).
8
DEF
Si chiama parallelogrammo ogni quadrilatero non intrecciato avente un centro di simmetria.
Detto M il centro di simmetria, le proprietà di
M
consentono di affermare che in un parallelogrammo ABCD:
i lati opposti sono paralleli e isometrici: AB // CD, AD // CB, [AB] > [CD] , [AD] > [CB];
gli angoli opposti sono isometrici: DAˆ B > BCˆ D , ABˆ C > CDˆ A ;
le diagonali si tagliano a metà: MA = MC , MB = MD .
Ciascuna delle precedenti proprietà è caratterizzante nel senso che un quadrilatero che gode di una qualsia
si di tali proprietà è un parallelogrammo (fig.23).
D
C
M
A
B
Parallelogrammo
Rettangolo
Rombo
Quadrato
(fig.23)
(fig.24)
(fig.25)
(fig.26)
Quando l'asse di ciascun lato è anche asse del lato opposto (fig.24), il parallelogrammo è un rettangolo.
Quando le diagonali sono assi di simmetria (fig.25), il parallelogrammo è un rombo.
Quando gli assi dei lati e le diagonali sono assi di simmetria (fig.26), il parallelogrammo è un quadrato.
A
M
B
D
C
centro di simmetria
(fig.27)
Conviene considerare anche il caso in cui i punti A, B, C, D sono allineati, come in fig.27. È subito chiaro che
le proprietà enunciate continuano a valere. Parleremo, in questo caso, di parallelogrammo degenere.
Y
Fissiamo ora in Π un riferimento cartesiano ortogonale OXY.
C
La (7) del paragrafo 3 può essere utilizzata per decidere se
D
un quadrilatero è un parallelogrammo, eventualmente degene
re. Il quadrilatero ABCD è un parallelogrammo se e solo se il
M
punto medio della diagonale [AC] coincide con il punto medio
A
della diagonale [BD] (fig.28). Infatti, se M è contemporanea
mente il punto medio delle due diagonali,
M
B
scambia fra loro
O
A con C e B con D.
(fig.28)
X
Sia A(xA, yA), B(xB, yB), C(xC, yC), D(xD, yD). Allora il punto medio di [AC] e il punto medio di [BD] hanno
coordinate
x A + xC
2
,
y A + yC
2
e
xB + xD
2
,
yB + yD
2
, rispettivamente. Ne segue che:
Il quadrilatero ABCD è un parallelogrammo, eventualmente degenere, se e solo se:
xA
yA
+ xC
= xB
+ xD
+ yC
= yB
+ yD
.
9
7. Gruppo delle traslazioni
Si chiama traslazione ogni isometria τ di Π in cui i punti o sono tutti fissi oppure si spostano tutti
DEF
in una stessa direzione, uno stesso verso e di un segmento di uguale lunghezza.
Assegnato un punto P, sia τ una traslazione del piano diversa dall'identità e
Q'
P'
sia P' = τ(P). Sia PP' la semiretta di origine P passante per P'. Se Q è un pun
to qualsiasi diverso da P e risulta Q' = τ(Q), allora Q' deve appartenere alla
semiretta di origine Q parallela ed equiversa alla semiretta PP'. Inoltre deve
essere QQ ′ = PP ′ . Quindi i punti P, P', corrispondenti in τ, consentono di in
Q
P
(fig.29)
dividuare il trasformato di un qualsiasi altro punto Q. In altre parole: una trasla
zione
τ
è completamente determinata da una coppia qualsiasi di punti corrispondenti in τ. Di più, la fig.29
suggerisce, con notevole efficacia intuitiva, che:
Se una traslazione τ manda P in P' e Q in Q', il quadrilatero PQQ'P' è un parallelogrammo.
Da questo risultato si deduce la seguente importante proposizione.
Una traslazione trasforma una retta in una retta ad essa parallela.
Dim.
Siano P, Q due punti qualsiasi del piano e sia τ una traslazione. Se P' = τ(P) e Q' = τ(Q), allo
ra PQQ'P' è un parallelogrammo. Poiché τ, essendo un'isometria, trasforma rette in rette, es
sa trasforma la retta PQ nella retta P'Q'. Ma queste due rette, su cui giacciono rispettivamen
te i lati opposti [PQ] e [P'Q'] del parallelogrammo PQQ'P', sono parallele.
Fissato ora in Π un riferimento cartesiano ortogonale OXY, sia τ la traslazione che manda l'origine O nel pun
to O'(h, k) (fig.30).
Dato un punto P(x, y), vogliamo determinare le coordinate (x', y') del punto P' = τ(P).
Sappiano che il quadrilatero OO'P'P è un parallelogrammo (eventualmente
degenere, cioè con i quattro punti allineati). Inoltre, la condizione che abbia
mo ricavato alla fine del paragrafo precedente, assicura che risulta:
Y
P'(x', y')
P(x, y)
0 + x′ = x + h
.
0 + y′ = y + k
O'(h, k)
Le uguaglianze x' = x + h e y' = y + k sono le equazioni della traslazione τ.
∴
È τ:
x′ = x + h
y′ = y + k
ovvero τ :
x′
y′
1 0 h
=
1
O
x
0 1 k ⋅ y
0 0 1
.
X
(fig.30)
1
Viceversa, si può dimostrare che ogni isometria di equazioni x' = x + h e y' = y + k è una traslazione.
Posto:
u=
da ora in poi indicheremo la traslazione con
h
k
,
τ u , e parleremo di traslazione di vettore u .
I numeri reali h e k si dicono le componenti della traslazione nel riferimento cartesiano adottato.
In particolare, se h = k = 0, si ottiene la traslazione nulla:
Indichiamo con T l'insieme delle traslazioni di Π.
τ 0 . È, ovviamente, τ 0 = iΠ.
10
( T, ) è un gruppo abeliano.
Dim.
Siano
h
τ u , τ v rispettivamente le traslazioni di vettori u =
τu :
x′
y′
1 0 h
x
τv :
= 0 1 k ⋅ y ,
1
0 0 1
1
k
e v=
p
q
.
1 0 p
x
= 0 1 q ⋅ y .
x′
y′
1
0 0
1
1
È sufficiente verificare che (T, ) è un sottogruppo abeliano del gruppo ( , ).
•
T è una parte stabile di
per l'operazione .
Anzitutto, le traslazioni sono isometrie. Allora T ⊆ . Si ha poi:
τ v τu :
1 0 p
= 0 1 q ⋅
x′
y′
1
0 0
1 0 h
1 0 h+p
x
=
0 1 k ⋅ y
0 0 1
1
1
0 0
∴ τ v τ u = τ u+ v .
•
x
.
0 1 k+q ⋅ y
1
1
(1 )
L'operazione su T è commutativa.
Infatti, si riconosce subito che
τ u τ v = τ v +u = τ u + v .
∴ τ v τu = τu τ v .
•
L'inversa di una traslazione è una traslazione.
Risulta:
τ −u τu :
Allora
x′
y′
=
1
1 0 −h
1 0 h
0 1 −k ⋅
0 0 1
0 1 k ⋅ y
0 0 1
1
1 0 0
x
=
x
0 1 0 ⋅ y
0 0 1
1
.
τ −u τu = τ 0 .
∴ τu−1
=
τ −u .
(2)
Osserviamo le (1) e (2). La prima ci dice che la composta delle traslazioni di vettori u e v è la traslazione di
vettore u + v ; la seconda, che l'inversa della traslazione di vettore u è la traslazione di vettore − u .
8. L'equazione cartesiana della retta
Fissato nel piano un riferimento cartesiano ortogonale OXY, una retta qualsiasi può essere rappresentata da
alcuni elementi che sono in relazione con il riferimento stesso.
Consideriamo la retta t asse del segmento [QQ'] i cui estremi sono simmetrici rispetto all'origine O (fig.31).
Y
t
Q(a, b)
P(x, y)
(fig.31)
X
O
Q'(−a, −b)
Se (a, b) sono le coordinate di Q, le coordinate di Q' saranno (−a, −b) (per la (7) del paragrafo 5).
La retta t è il luogo dei punti equidistanti da Q e da Q'. Pertanto, se P(x, y) è un punto qualsiasi di t, risulta
PQ = PQ ′ . Allora, facendo intervenire l'espressione cartesiana della distanza, si ha:
( x − a ) 2 + ( y − b) 2 =
( x + a) 2 + ( y + b ) 2
(1)
11
da cui, con qualche passaggio, si ottiene:
ax + by = 0
(2)
Tutti i punti della retta t hanno coordinate che sono soluzioni di questa equazione in x e y. Di più, osserviamo
che tutti i passaggi algebrici eseguiti per andare dalla relazione iniziale (1) a quella finale (2) si possono inver
tire. Allora la (2) esprime il fatto che il punto P(x, y) ha uguale distanza da Q(a, b) e da Q'(−a, −b).
∴
Ogni equazione lineare della forma (2), con a e b non entrambi nulli, rappresenta una retta passante
per l'origine, asse del segmento [QQ'], con Q(a, b) e Q'(−a, −b).
Consideriamo ora la traslazione di vettore u =
h
k
, cioè la traslazione
O'(h, k). Indicando con (x, y) le coordinate di un punto P ∈ t, con (x', y')
τu che manda l'origine O nel punto
Y
le coordinate del punto P' = τu (P), la retta t viene trasformata nella
O'(h, k)
retta r che passa per i punti O' e P' ed è parallela a t (fig.32).
Allora
τu :
x′ = x + h
y′ = y + k
, da cui
τ u−1 :
x = x′ − h
y = y′ − k
r
P'
e sostituendo
nell'equazione (2), si ottiene a(x – h) + b(y – k) = 0, che si può scrive
t
P
X
O
(fig.32)
re ax' + by' – ah – bk = 0. Da questa, ponendo c = – ah – bk e soppri
mendo gli apici, si ottiene:
ax + by + c = 0
∴
(3)
Ogni retta del piano si può rappresentare con un'equazione lineare del tipo (3), con a e b non entram
bi nulli. Viceversa, ogni equazione del tipo (3), con a e b non entrambi nulli, rappresenta una retta.
La (3) prende il nome di equazione cartesiana della retta.
Per indicare che la retta r ha equazione ax + by + c = 0, scriveremo r : ax + by + c = 0.
In particolare, se c = 0, la retta passa per l'origine. Se b = 0, dalla (3) si ricava x = − ac , che rappresenta la
retta parallela all'asse Y che incontra l'asse X nel punto di ascissa − ac . Infine, se a = 0, dalla (3) si deduce
y = − bc , che rappresenta la retta parallela all'asse X che incontra l'asse Y nel punto di ordinata − bc .
Osserviamo che tutte le rette che si ottengono tenendo fissi a e b e dando valori diversi a c sono parallele fra
loro, essendo tutte parallele a t. Inoltre è importante notare che, se si moltiplicano a, b, c per uno stesso nu
mero reale diverso da zero, l'equazione ottenuta è equivalente alla (3) e perciò rappresenta la stessa retta r.
Vediamo alcuni importanti teoremi.
Se r : ax + by + c = 0 e s : a ′x + b ′y + c ′ = 0 , allora le rette r, s sono incidenti se e solo se:
a b
∈ GL(2, IR).
a′ b′
Dim.
(4)
Sia r ∩ s = {P0}. Per determinare le coordinate di P0 basta risolvere il sistema lineare in x, y:
ax + by = − c
.
a′x + b′y = − c′
Questo ha soluzione unica se e solo se la matrice dei coefficienti è non singolare.
12
Dette (x0, y0) le coordinate del punto d'incidenza P0 delle rette r e s, dalla formula di Cramer si ha subito:
x0
y0
=
b′ − b
−c
1
⋅
.
ab′ − a′b − a′
a
− c′
(5)
Inoltre, dal teorema precedente, si deduce la condizione di parallelismo di r e s:
a b
= 0,
a′ b′
r // s ⇔
∀ r, s ∈
.
(6)
Dati due punti distinti P(x1, y1) e Q(x2, y2), l'equazione cartesiana della retta PQ è:
Dim.
x1
y1
1
x2
y2
1
x
y
1
= 0.
(7)
Lo sviluppo in cofattori relativo alla terza riga del determinante al primo membro fornisce:
x⋅
y1 1
x
1
x1
− y⋅ 1
+
y2 1
x2 1
x2
y1
= 0,
y2
che è un'equazione lineare in x, y. Di più, le coordinate di P e Q verificano l'eq. (7) essendo
x1
y1
1
x2
y2
1 = 0 e
x1
y1
1
x1
y1
1
x2
y2
1 = 0. Quindi la retta di eq. (7) passa per i punti P e Q.
x2
y2
1
Da questo teorema segue subito la condizione di allineamento di tre punti P(x1,y1), Q(x2,y2), R(x3,y3), data da:
x1
y1
1
x2
x3
y2
y3
1
1
= 0.
(8)
9. Forma esplicita e forma punto−pendenza
Sia r : ax + by + c = 0. Se b ≠ 0, cioè se la retta r non è parallela all'asse Y, dall'equazione di r si ricava
y = − ba x − bc da cui, ponendo − ba = m e − bc = q, si ottiene:
y = mx + q
(1)
La (1) prende il nome di forma esplicita dell'equazione dalla retta.
Il numero reale m si chiama pendenza o coefficiente angolare di r. Dalla (6) del paragrafo 8, segue subito
che due rette r e s hanno la stessa pendenza se e se se sono parallele.
Osserviamo che q è l'ordinata del punto in cui r incontra l'asse Y. Infatti, la coppia (0, q) soddisfa l'equazione
(1). Ciò giustifica il nome di ordinata all'origine che comunemente si dà a q.
Quando m = 0, l'equazione (1) si riduce a y = q e la retta è parallela all'asse X; quando q = 0, l'equazione di
venta y = mx e la retta passa per l'origine degli assi.
Vogliamo ribadire che le rette parallele all'asse Y non possono essere rappresentate nella forma (1), mentre
la forma ax + by + c = 0 permette di rappresentare ogni retta. Per questo motivo quest'ultima viene detta for
ma generale dell'equazione della retta.
Ora, se P(x0, y0) è un punto qualsiasi della retta r di equazione (1), deve essere y0 = mx0 + q e, sottraendo
questa dalla (1) membro a membro, con qualche passaggio si ricava:
y − y0 = m(x − x0)
(2)
13
Come subito si riconosce, tutti e solo i punti della retta r hanno coordinate che verificano questa equazione.
La (2) viene detta forma punto–pendenza dell'equazione di r.
È interessante notare che la (2) rappresenta l'insieme delle rette che passano per il punto P(x0, y0) al variare
della pendenza, tranne la retta parallela all'asse Y. Infatti, la (2) è verificata dalle coordinate (x0, y0) del punto
P qualunque sia il valore di m.
10. Rette perpendicolari fra loro
Sappiamo che l'asse del segmento [QQ'] di estremi Q(a, b) e Q'(−a,−b) è la retta t : ax + by = 0. Di più, sap
piamo che t è perpendicolare alla retta r passante per i punti Q e Q'.
Ora, indicata con m la pendenza di t, m = −
a
b
, è immediato verificare che il punto P(1, m) appartiene a t. Allo
ra, per la simmetria centrale di centro O, anche il punto P'(−1, −m) appartiene a t (fig.33).
r
Y
t
r = QQ'
Q(a, b)
P'(−1, −m)
t = PP'
P(1, m)
X
O
t⊥r
Q'(−a, −b)
(fig.33)
Ciò premesso, determiniamo la pendenza di r, indicata con m'. Da t ⊥ r, segue r ⊥ t, perché la relazione
di ortogonalità è simmetrica. Allora r è l'asse del segmento [PP'] e, di conseguenza, la sua equazione è
1x + my = 0. Ne segue:
m′ = −
∴
1
m
(1)
Due rette sono perpendicolari fra loro se e solo se le loro pendenze sono antireciproche.
11. La parabola
DEF
Si chiama parabola il luogo dei punti del piano equidistanti da una retta fissa d, detta direttrice,
e da un punto fisso F∉ d, detto fuoco.
Y
Indicata con D la proiezione ortogonale di F su d, assumiamo
come asse Y la retta orientata DF in cui D precede F; come
P(x, y)
asse X la parallela alla direttrice nel punto medio O del segmen
to [DF]. Se ora poniamo d(O,F) = p, chiamata distanza focale,
le coordinate di F sono ( 0, p ) e la direttrice avrà equazione
F
y = −p. Ciò premesso, per ogni punto P(x, y) appartenente alla
O
parabola, detta H la proiezione ortogonale di P su d (fig.34), si
D
ha, per definizione, PH = PF . E' allora:
y+p =
x 2 + (y − p )2
X
H
(fig.34)
da cui, quadrando e riducendo i termini simili, si deduce:
y =
chiamata equazione canonica della parabola.
1
4p
⋅ x2
(1)
d
14
Osserviamo che un'isometria f trasforma una parabola
in una parabola
': infatti la definizione di para
bola si basa sull'uguaglianza di due distanze e le isometrie conservano le distanze. Allora un punto P che
sulla parabola
è equidistante dal fuoco F e dalla direttrice d, viene trasformato, da f, in un punto P'
equidistante dal punto F' = f(F) e dalla retta d' = f(d). Quindi P' ∈
Di più, dall'equazione (1) si riconosce subito che
rabola
, anche il punto P'(−x, y) appartiene a
y(
' = f( ).
). Infatti, se un punto P(x, y) appartiene alla pa
. Questo perché il fattore x è al quadrato e quindi non
cambia al cambiare del segno di x. L'asse Y è allora asse di simmetria di . Il punto d'intersezione della
parabola con il suo asse, cioè l'origine O, si dice vertice della parabola.
Vediamo come cambia l'equ. (1) di una parabola
X
:
x′ =
x
y′ = − y
, da cui
X
−1
:
x′
y = − y′
x =
per effetto della simmetria assiale di asse X. Si ha:
Y
e sostituendo nella
equazione (1), si ottiene − y ′ = 41p ⋅ x ′ 2 da cui, moltiplicando
d'
O
ambo i membri per −1 e sopprimendo gli apici, segue:
y = − 41p ⋅ x 2
X
F'
(2)
Dalle equazioni (1) e (2) si desume che l'equazione canonica
(fig.35)
della parabola è del tipo:
y = ax2
(3)
Il coefficiente a si chiama apertura della parabola. Quando a = 41p , è a > 0; quando a = − 41p , è a < 0.
Nel primo caso, diciamo che la parabola volge la concavità verso l'alto (cioè verso il semiasse positivo del
le ordinate, come in fig.34); nel secondo, diciamo che la parabola volge la concavità verso il basso (fig.35).
Vediamo come cambia l'equ. (3) di una parabola
per effetto della traslazione
nel punto O'(h, k) (fig.36). Si ha:
τu :
x′ = x + h
,
y′ = y + k
da cui τ −1 :
u
τu che manda il vertice O
Y
x = x′ − h
y = y′ − k
e sostituendo nel
la equazione (2), si ottiene y' − k = a ⋅ (x' − h)2 ovvero:
y' = ax2 − 2ahx' + ah2 + k.
O'
Questa, ponendo b = − 2ah, c = ah2 + k e sopprimendo gli apici,
O
(fig.36)
diventa:
y = ax2 + bx + c
X
(4)
chiamata equazione generale della parabola (con l'asse parallelo all'asse Y).
2
Osserviamo infine che, per le posizioni fatte, è h = − b e k = 4ac4−a b = − 4∆a , dove ∆ = b2 – 4ac.
2a
Quindi la parabola ': y = ax2 + bx + c si ottiene dalla parabola : y = ax2 mediante la traslazione di vet
tore u = ( −
L'asse di
b
2a
, − 4∆a ). Il vertice di
' è allora il punto O'( − 2ba , − 4∆a ) e il fuoco F'( − 2ba , 14−a∆ ).
' ha equazione x = − 2ba e la direttrice y =
− 1+ ∆ .
4a
15
12. L'ellisse
DEF
Si chiama ellisse il luogo dei punti del piano per i quali è costante la somma delle distanze da
due punti fissi F1 e F2 detti fuochi.
Y
Assumiamo come asse X la retta F1F2, orientata da F1 a F2, e
P
Come asse Y la perpendicolare a X nel punto medio O del
segmento
[F1 F2].
Se ora poniamo d (F1, F2) = 2c, chiamata
distanza focale, le coordinate di F1 e F2 sono rispettivamente
F1
O
F2
X
(−c,0) e (c,0). Così, per ogni punto P(x, y) appartenente all'ellis
se, poniamo:
con a > c (fig.37).
F1P + PF2 = 2a
(1)
(fig.37)
La (1), tenendo presente la formula della distanza di due punti, diventa:
( x + c ) 2 + y 2 + ( x − c ) 2 + y 2 = 2a
(2)
Questa equazione, soddisfatta da tutti e solo i punti dell'ellisse, può essere scritta in una forma più semplice
portando al secondo membro la seconda radice, elevando poi ambo i membri al quadrato e riducendo i termi
ni simili. Si ottiene:
a 2 − cx = a ⋅ ( x − c ) 2 + y 2 .
Quadrando nuovamente, si deduce:
(a 2 − c 2 ) ⋅ x 2 + a 2 y 2 = a 2 ⋅ (a 2 − c 2 ) .
Successivamente, ponendo a2 − c2 = b2 ( si può fare, perché a > c ), l'equazione diventa b2x2 + a2y2 = a2b2 da
cui, dividendo tutto per a2b2, si ricava:
2
x2 + y = 1
a2 b2
(3)
chiamata equazione canonica dell'ellisse.
Nell'equazione (3) le variabili x e y figurano soltanto al quadrato. Quindi l'ellisse è una curva unita per cia
scuna delle simmetrie:
X
:
x′ = x
y′ = − y
,
Y
:
x′ = − x
y′ = y
,
O
:
x′ = − x
.
y′ = − y
Per questo, gli assi di simmetria X, Y si dicono assi dell'ellisse; l'origine O si chiama centro dell'ellisse.
Per y = 0, è x = ±a; per x = 0, è y = ±b. Quindi l'ellisse incontra gli assi nei punti A1(−a, 0 ), A2( a, 0 ),
B1(0,−b), B2(0,b), detti vertici. Il segmento [A1A2] si chiama asse focale o asse maggiore dell'ellisse; il
segmento [B1B2] costituisce l'asse minore, perché è sempre a > b. I segmenti [OA2], [OB2] si chiama
no rispettivamente semiasse focale (o semiasse maggiore) e semiasse minore.
Per a = b, posto r = a, l'equazione (3) diventa:
x2 + y2 = r 2
(4)
che è l'equazione della circonferenza di centro O e raggio r.
Essendo ora c2 = a2 − b2 = 0, i fuochi dell'ellisse coincidono ora con il centro O della circonferenza.
16
Vediamo come cambia l'equ. (4) di una circonferenza
per effetto della traslazione τ u che manda il cen
tro O nel punto T(h, k) (fig.38). Si ha:
τu :
x′ = x + h
, da cui τ −1 :
u
y′ = y + k
(4), si ottiene:
Y
x = x′ − h
y = y′ − k
(x ′ − h)2 + (y ′ − k )2
e sostituendo nella
T
k
= r2 .
da cui, sviluppando e sopprimendo gli apici, si ricava:
O
x 2 + y 2 − 2hx − 2ky + h 2 + k 2 − r 2 = 0 .
2
2
h
X
(fig.38)
2
Questa, ponendo α = −2h, β = −2k, γ = h + k − r , diventa:
x2 + y2 + αx + βy + γ = 0
(5)
chiamata equazione normale della circonferenza di centro T e raggio r.
Un'altra relazione interessante fra a e c si chiama eccentricità dell'ellisse ed è definita da:
ε = ac
def
Il nome stesso suggerisce che ε può assumersi come una misura di quanto l'ellisse, per la sua forma più
o meno allungata, differisce dalla circonferenza. Quando F1 = F2, è c = 0, l'ellisse è una circonferenza e ri
sulta ε = 0. Quando d (F1, F2) = 2a, è c = a e quindi i fuochi coincidono con i vertici. In questo caso, l'ellis
se degenera in un segmento e risulta ε = 1. In tutti i casi intermedi, ε è compresa fra 0 e 1, perché c < a.
13. L'iperbole
DEF
Si chiama iperbole il luogo dei punti del piano per i quali è costante, in valore assoluto, la diffe
renza delle distanze da due punti fissi F1 e F2 detti fuochi.
Y
Posto d (F1,F2) = 2c, per ogni punto P appartenente all'iperbole, po
niamo:
F1P − PF 2 = 2a
oppure
F2P − PF1 = 2a
(1)
P
con 0 < a < c. Ciascuna di queste due relazioni è verificata da infiniti
punti, ma nessuno dei punti che verificano la prima relazione verifi
ca anche la seconda, e inversamente. Quindi l'iperbole è l'unione di
due parti disgiunte, chiamate rami dell'iperbole (fig.39).
Fissato il sistema di riferimento come si è fatto per l'ellisse e con
passaggi analoghi a quelli svolti allora, si ricava:
F1
F2
X
(fig.39)
2
x2 − y = 1
a2 b2
(2)
dove b2 = c2 − a2, chiamata equazione canonica dell'iperbole.
Nell'equazione canonica dell'iperbole le variabili x e y figurano soltanto al quadrato. Quindi l'iperbole, co
me l'ellisse, è una curva unita per ciascuna delle simmetrie
X,
Y,
O.
Per questo, gli assi di simmetria X
e Y si dicono assi dell'iperbole. In particolare, X si dice asse focale e Y asse ideale. L'origine O si chia
ma centro dell'iperbole.
17
Per y = 0, è x = ±a. Quindi l'iperbole incontra l'asse focale nei punti A1(−a,0), A2(a,0), detti vertici.
Per x = 0, y ∉ IR. Quindi l'iperbole non incontra l'asse ideale.
Le rette per l'origine O in fig.39 hanno equazioni y = ba x , y = − ba x e si chiamano asintoti dell'iperbole.
La loro caratteristica è che si avvicinano sempre più all'iperbole, senza mai toccarla, quando ci si allonta
na verso l'infinito (*).
Per a = b, l'equazione (2) diventa:
x2−y2 = a2
(3)
e l'iperbole si dice equilatera. Osserviamo che gli asintoti di un'iperbole equilatera, cioè le rette di equa
zioni y = x e y = −x, coincidono con le bisettrici degli assi e quindi sono fra loro perpendicolari.
(*) La parola asintoto significa senza contatto. Intuitivamente, l'asintoto a una curva si comporta come se
fosse tangente alla curva in un punto posto all'infinito. Rette di questo tipo saranno studiate dettagliata
mente in seguito.