Il lavoro del Campo elettrico
Obiettivi
Confrontare l’espressione classica dell’energia con quella relativistica
Riconoscere la validità del principio di conservazione dell’Energia anche in ambito relativistico
Passare dal registro grafico a quello analitico e viceversa
Qual è l’energia cinetica acquistata da una particella carica q , che parte dalla quiete in un campo elettrico
uniforme, quando si muove attraverso una d.d.p. ?
a)Se la particella è un elettrone e
, quale sarà il valore dell’energia cinetica dell’elettrone e
della sua velocità secondo la Fisica classica? E secondo la Relatività?
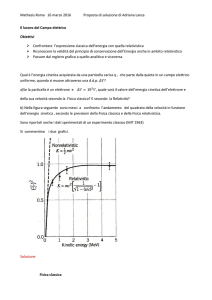
b) Nella figura seguente sono messi a confronto l’andamento del quadrato della velocità in funzione
dell’energia cinetica , secondo le previsioni della Fisica classica e della Fisica relativistica.
Sono riportati anche i dati sperimentali di un esperimento classico (MIT 1963)
Si commentino i due grafici.
Interpretazione relativistica del Campo Magnetico
(adattamento da Bergamaschini-Marazzini-Mazzoni- Fisica 3 Carlo Signorelli Editore)
Obiettivi
Osservare , mediante un esempio, che è possibile che in un riferimento il campo sia puramente
magnetico o puramente elettrico, mentre nell'altro si osservino entrambi.
Applicare le leggi della Relatività speciale
Riconoscere che il Principio di relatività , nell’ambito della Fisica classica, non è rispettato dai
fenomeni elettromagnetici
Una carica positiva q è posta , in quiete, a distanza r da un filo di lunghezza L, su cui è distribuita
uniformemente una carica Q anch’essa positiva (r<<L Densità lineare = Q/L = λ )
Per un osservatore O, solidale con q e con la distribuzione di cariche , sulla carica q agisce una forza
elettrica , dipendente
dalla carica q
dalla distanza r
dalla densità lineare di carica , λ, della distribuzione
a)Si determini
b) Quale sarebbe la risultante delle forze, applicate alla carica q , dal punto di vista di un osservatore O’in
moto rispetto ad O?
(La velocità di O’ è opposta a
quella delle cariche, indicata in
figura.)
c) Si studi lo stesso fenomeno
secondo le leggi della Relatività
speciale
Elettroni veloci
( adattamento da Battimelli-Stilli Le vie della Fisica Vol. 3- Laterza)
Obiettivi
Confrontare le leggi e le formule della Fisica classica con quelle corrispondenti della Fisica
relativistica nell’ambito della Meccanica e nell’Elettromagnetismo
Utilizzare le approssimazioni in modo consapevole
L’acceleratore lineare di Stanford porta un fascio di elettroni all’energia di 40 GeV, accelerandoli lungo un
tubo rettilineo lungo 3 km; gli elettroni acquistano dunque, lungo il percorso, un’energia pari a 13,3 MeV
per ogni metro.
a) Se fosse valida l’espressione classica dell’energia cinetica
, quanto spazio dovrebbero
percorrere gli elettroni nel tubo dell’acceleratore per raggiungere la velocità della luce?
b) In realtà gli elettroni che emergono all’estremità dell’acceleratore hanno una velocità v minore di
quella della luce ma molto prossima a c.
Quanto vale il rapporto
Se un raggio di luce e uno di questi elettroni facessero una corsa su un tratto di 10 km, quale
sarebbe il vantaggio del raggio luminoso sull’elettrone?
c) Quanto risulta lungo l’acceleratore per un osservatore solidale con il riferimento degli elettroni?
d) Se si volesse accelerare il fascio di elettroni utilizzando un ciclotrone <<classico>> in cui il campo
magnetico B è uguale a 1T, assumendo
il valore della velocità oltre il quale la trattazione
classica non dà più un’approssimazione soddisfacente, quale dovrebbe essere il suo raggio
massimo ? Quale sarebbe la correzione tenendo conto degli effetti relativistici?
Tenendo conto degli effetti relativistici, quale dovrebbe essere il raggio massimo del ciclotrone se gli
elettroni avessero energia pari a 40 GeV?