Esercizio 10-11-15-16-17 - e-Learning

Esercizio 10
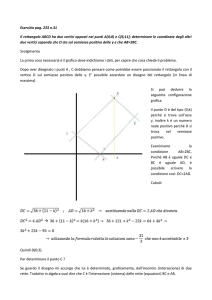
Data una retta AB e due punti C e D nello stesso semipiano, con riga e compasso trovare un punto X sulla
̂ = 𝐵𝑋𝐷
̂ . In un bigliardo colpire con la biglia bianca quella rossa dopo una sponda,
retta AB tale che 𝐴𝑋𝐶
due sponde, tre sponde,...
Dopo quattro sponde ripassa per lo stesso punto
Occorre tracciare la perpendicolare alla retta AB passante
per C e poi per D.
Tracciamo una circonferenza di centro C e raggio opportuno
così da poter individuare le sue intersezioni con la retta AB
(chiamiamo queste intersezioni P e Q). Successivamente
tracciamo altre due circonferenze di raggio PC=QC centrate
in P e inQ. Il punto di intersezione (R) tra queste ultime
circonferenzee che si affianca a C permette di ottenere la retta perpendicolare CK.
Centriamo in K con raggio KC e troviamo il punto di intersezione C1 con la perpendicolare CK.
Analogamente procediamo per il punto D e troviamo il punto D1.
Uniamo C con D1 e D con C1. Il punto X intersezione tra le due rette si trova anche sulla retta AB e soddisfa
̂1 che sono angoli opposti al vertice e
̂1 e di 𝐶𝑋𝐶
la richiesta dell’esercizio in quanto AB è bisettrice di 𝐷𝑋𝐷
̂ = 𝐵𝑋𝐷
̂
quindi 𝐴𝑋𝐶
Esercizio 11
Con riga e compasso bisecare un angolo il cui vertice non si trova nel foglio di disegno.
Date le rette passanti per A e B con
punto di incontro C esterno al foglio.
Consideriamo A e B i punti di
frontiera.
Tracciamo la parallela alla retta AC
passante per B e la parallela alla BC passante per A. Chiamiamo D il punto di intersezione .
Tracciamo una circonferenza di centro D che interseca le rette DA e DB rispettivamente in P e in Q.
Poi, puntando dapprima in P e poi in Q e con raggio PQ, tracciamo le due circonferenze che hanno
̂ ed
in comune il punto R. La semiretta di origine D e passante per R è la bisettrice dell’angolo 𝐵𝐷𝐴
è anche la bisettrice dell’angolo C.
Esercizio 15
I lati di un triangolo X sono uguali alle mediane di un triangolo Y. Dimostrare che l’area di X è 3/4 dell’area
di Y.
Penso di possa risolvere con la formula di Erone 𝐴𝑟𝑒𝑎 𝑡𝑟𝑖𝑎𝑛𝑔𝑜𝑙𝑜 = √𝑝(𝑝 − 𝑎)(𝑝 − 𝑏)(𝑝 − 𝑐) con p il
2
semiperimetro e a,b,c i tre lati. Dal teorema della mediana abbiamo che 2𝑚𝑎𝑐
= 𝐴𝐵2 + 𝐵𝐶 2 −
𝐴𝐶 2
2
Esercizio 16
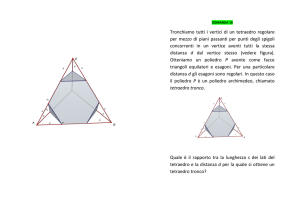
Calcolare il volume di un tetraedro regolare in funzione del lato 𝑎.
Il tetraedro regolare è formato da 4 triangoli equilateri con 𝐴𝑟𝑒𝑎 𝑏𝑎𝑠𝑒 =
𝑎√6
3
dove h è l’altezza del tetraedro da cui Volume
1
12
𝑎2 √3
4
dove a è il lato, ℎ =
𝑎3 √2
Calcolare il volume di un ottaedro regolare in funzione del lato 𝑎
L’ottaedro regolare è costituito da 8 facce costituite da triangoli isosceli il suo volume è quattro
4
1
volte quello del tetraedro regolare da cui Volume 12 𝑎3 √2 = 3 𝑎3 √2
Esercizio 17
Utilizzando la formula di Eulero V - L + F = 2, mostrare che in ogni decomposizione di una sfera in pentagoni
ed esagoni, i pentagoni sono 12.
È impossibile coprire una sfera soltanto con esagoni, anche non regolari, per formare una geode,
poiché tale copertura non rispetterebbe la formula di Eulero per i poliedri. Infatti, in un poliedro a
facce soltanto esagonali, ogni vertice è comune a 3 facce ed ogni spigolo a 2 facce. Poiché qualsiasi
esagono ha 6 lati e 6 vertici, tale poliedro deve dunque avere 6/3 vertici per faccia e 6/2 spigoli per
faccia. Dunque, se F è il numero di facce, i numeri di spigoli S devono essere uguali a 3F ed il
numero di vertici V a 2F. Si ha allora:
e la formula di Eulero non è verificata.
Invece, sostituiamo alcuni esagoni di questa impossibile copertura con pentagoni. Se il numero di
facce non varia, il numero di spigoli e di vertici diminuisce: per ogni pentagono aggiunto, si ha
(6 - 5)/2 spigoli, cioè un metà-spigolo in meno e (6 - 5)/3 vertici, cioè un terzo di vertice in meno;
aumenta dunque ogni volta della differenza, cioè di un sesto. Affinché la formula di
Eulero per i poliedri sia rispettata, occorre che
inizialmente a 0, diventi uguale a 2,
dunque aumenta di 12/6. In breve, occorre sostituire 12 esagoni con altrettanti pentagoni. Il numero
dei vertici V è allora di 2F- 4 e quello degli spigoli S di 3F- 6.