rette

Esercizio pag. 233 n.31
Il rettangolo ABCD ha due vertici opposti nei punti A(4;0) e C(6;11); determinare le coordinate degli altri
due vertici sapendo che D sta sul semiasse positivo delle y e che AB=2BC.
Svolgimento
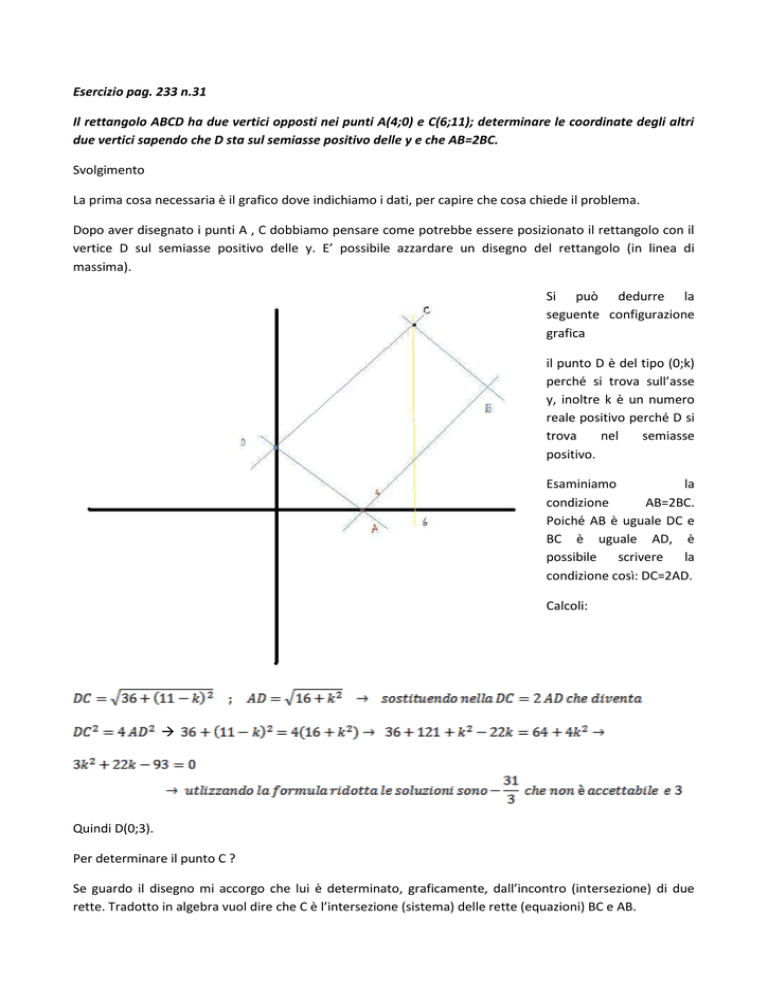
La prima cosa necessaria è il grafico dove indichiamo i dati, per capire che cosa chiede il problema.
Dopo aver disegnato i punti A , C dobbiamo pensare come potrebbe essere posizionato il rettangolo con il
vertice D sul semiasse positivo delle y. E’ possibile azzardare un disegno del rettangolo (in linea di
massima).
Si può dedurre la
seguente configurazione
grafica
il punto D è del tipo (0;k)
perché si trova sull’asse
y, inoltre k è un numero
reale positivo perché D si
trova
nel
semiasse
positivo.
Esaminiamo
la
condizione
AB=2BC.
Poiché AB è uguale DC e
BC è uguale AD, è
possibile
scrivere
la
condizione così: DC=2AD.
Calcoli:

Quindi D(0;3).
Per determinare il punto C ?
Se guardo il disegno mi accorgo che lui è determinato, graficamente, dall’incontro (intersezione) di due
rette. Tradotto in algebra vuol dire che C è l’intersezione (sistema) delle rette (equazioni) BC e AB.
Le equazioni delle suddette rette sono:
BC: (retta passante per C e perpendicolare alla retta DC) 3x+4y-62=0
AB: (retta retta passante per A e parallela alla retta DC) 4x-3y-16=0
Sistema tra le rette BC e AB
Il punto B è (10;8)
Esercizio pag. 233 n. 32
I punti A(-1;-2) e B(1;2) sono vertici consecutivi di un rombo; determinare la misura dell’area del rombo
sapendo che la diagonale maggiore AC sta su una retta di coefficiente angolare 1.
Suggerimenti per risolvere
Grafico
Retta ( r )per A di m=1
Retta ( s ) per B perpendicolare alla retta r
Punto M intersezione di r ed s
Determinare C sulla r tale che AM=MC (IMPORTANTE: il punto C ha coordinate ordinta k e ascissa si deduce
dalla retta)
Per trovare D si ragiona come per il punto C