ECONOMIA POLITICA I (Prof. S. Vergalli)
ESERCITAZIONE SU TEORIA DELLA PRODUZIONE
E MINIMIZZAZIONE DEI COSTI
1) Facendo riferimento alla seguente tabella, che descrive la funzione di produzione di un’impresa (ogni
casella rappresenta il livello produttivo corrispondente a dati livelli di utilizzo di capitale e lavoro), indicate se
si hanno rendimenti di scala crescenti, decrescenti o costanti.
3K
2K
1K
55
50
40
1L
100
80
50
2L
120
100
55
3L
a) Argomentate brevemente la vostra risposta.
b) Facendo riferimento alla tabella, discutete se la seguente affermazione e’ vera o falsa e spiegate il
perché: ”La produttività marginale di ciascun fattore produttivo e’ decrescente”.
c) Per una funzione di produzione continua con le proprietà indicate nei punti a) e b), rappresentate
graficamente l’andamento della funzione di costo medio variabile di breve periodo (tenendo fisso il capitale)
e l’andamento della funzione di costo medio di lungo periodo dell’impresa in questione.
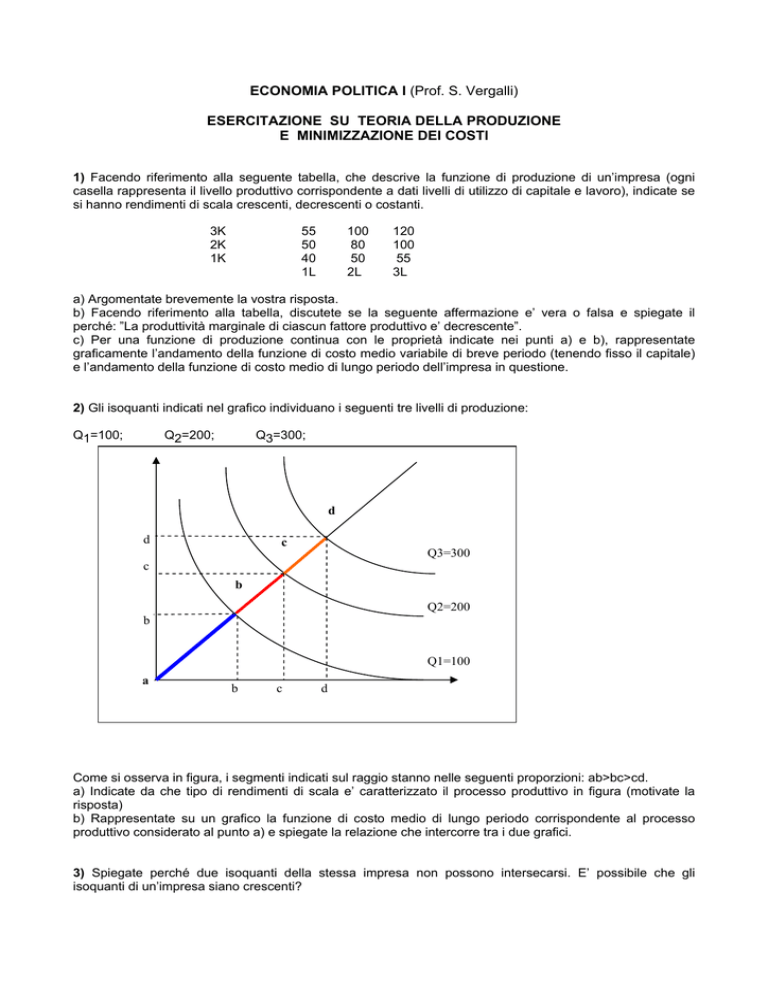
2) Gli isoquanti indicati nel grafico individuano i seguenti tre livelli di produzione:
Q1=100;
Q2=200;
Q3=300;
d
d
c
Q3=300
c
b
Q2=200
b
Q1=100
a
b
c
d
Come si osserva in figura, i segmenti indicati sul raggio stanno nelle seguenti proporzioni: ab>bc>cd.
a) Indicate da che tipo di rendimenti di scala e’ caratterizzato il processo produttivo in figura (motivate la
risposta)
b) Rappresentate su un grafico la funzione di costo medio di lungo periodo corrispondente al processo
produttivo considerato al punto a) e spiegate la relazione che intercorre tra i due grafici.
3) Spiegate perché due isoquanti della stessa impresa non possono intersecarsi. E’ possibile che gli
isoquanti di un’impresa siano crescenti?
4) La seguente tabella contiene alcuni dati sui costi di lungo periodo della American Production Company.
Volume di
Costo
Costo
Costo
produzione
totale
medio
marginale
50
..........
$1000
51
$52000
...........
.................
52
............
$1040
.................
53
............
..........
$5000
a) Completare la tabella.
b) In corrispondenza dei volumi di produzione indicati, la tecnologia utilizzata dall’impresa e’ caratterizzata
da rendimenti di scala crescenti, decrescenti o costanti?
5) Si consideri la seguente funzione di produzione
y=f(x1, x2)=log(x1+1)+x2
a) Se un’impresa impiega la combinazione di input (x1, x2)=(2,5) e decide di raddoppiare la scala di
produzione, di quanto aumenta il livello di output?
b) Confrontare i saggi marginali di sostituzione corrispondenti alle combinazioni di input (x1, x2)=(2,5) e (x1,
x2)=(4,10).
c) Indicando con (w1, w2) i prezzi degli input e supponendo fisso il livello dell’output pari a y=y, sapete
ottenere la funzione di domanda dell’input x2 che minimizza i costi di produzione ?
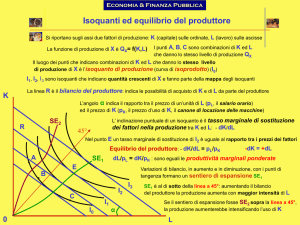
5) Partendo da una posizione di equilibrio iniziale E, si indichi la nuova combinazione ottimale dei fattori
capitale e lavoro per un’impresa che minimizza i costi per un dato livello produttivo (Q0 nella figura) nel
caso di diminuzione del prezzo del fattore lavoro.
In quale direzione variano le quantità impiegate di lavoro e capitale e le rispettive produttività marginali?
7) Nadia vende computer. La sua funzione di produzione e’ f(A,B)=A+2B, dove A e’ l’ammontare di lavoro
non specializzato e B l’ammontare di lavoro specializzato che lei impiega.
a) Riportate in grafico gli isoquanti delle combinazioni di input che consentono di produrre rispettivamente 20
e 40 computer.
b) La funzione di produzione di Nadia esibisce rendimenti di scala crescenti, costanti o decrescenti?
Giustificate la risposta.
c) Se Nadia usasse solo lavoro non specializzato, quante unita’ di tale input le occorrerebbero per produrre
Y computer?
d) Se il prezzo dei due fattori di produzione fosse (1,1), quale sarebbe la combinazione di fattori più
conveniente per produrre 20 computer? (Suggerimento: tracciate il vincolo di bilancio nel grafico precedente)
8) Si consideri un’impresa che dispone della seguente tecnologia Y=2√LK, che le consente di produrre il
bene Y (il cui prezzo non e’ noto), utilizzando gli input lavoro e capitale (i cui prezzi sono entrambi pari a 12).
a) Determinare le curve di isocosto dell’impresa;
b) Determinare la scelta ottimale dell’impresa, posto che voglia produrre Y=200.
c) A quanto ammonterà il profitto in tal caso?
9) Perché la ghiaia viene prodotta a mano in Nepal e meccanicamente negli Stati Uniti?