Università degli Studi di Bergamo — Facoltà di Ingegneria
Matematica I — Appello del 17 Gennaio 2007 Tema A
Cognome e Nome
Matr.
1.1. Dire se la seguente serie converge ed in caso affermativo calcolarne la somma
+∞
X
1
n
2
n=0
Svolgimento:
n
quindi la serie proposta è una serie geometrica. La ragione è
Abbiamo 21n = 21
minore di 1. La serie è quindi convergente e di somma
1
1−
1
2
=
1
1
2
1
2
ed è quindi di valore assoluto
= 2.
1.2. Risolvere nel campo complesso la seguente equazione
z3 = 1 + i
Svolgimento:
Abbiamo |1 + i|2 = 1 + 1 = 2, dunque la forma trigonometrica di 1 + i è:
√
√ 1
i
π
π √ iπ
1+i= 2 √ + √
= 2 cos + i sin
= 2e 4
4
4
2
2
√ 1 π4 +2kπ
√ 9π
√ π √
π
2π
Di conseguenza le soluzioni dell’equazione sono ( 2) 3 ei 3
con k = 1, 2, 3 cioè 6 2ei 12 , 6 2ei( 12 + 3 ) = 6 2ei 12 e
√ 17π
√
4π
π
6
2ei( 12 + 3 ) = 6 2ei 12 .
1.3. Calcolare il seguente limite
lim
x→+∞
x + 2 log x
arctan x
Svolgimento:
Abbiamo lim x = +∞ e lim log x = +∞, per cui lim (x + 2 log x) = +∞. Inoltre lim arctan x =
x→+∞
x→+∞
x→+∞
lim
x→+∞
x→+∞
π
2
x + 2 log x
= +∞.
arctan x
1.4. Calcolare l’integrale
Z
0
1
1
arctan x dx
1 + x2
Svolgimento:
La derivata di arctan x è
Z
0
1
1
1+x2
quindi
x=1
1
1
1
1
1 π 2 1 2
π2
2
2
2
− 0 =
arctan
x
dx
=
(arctan
x)
=
(arctan
1)
−
(arctan
0)
=
.
2
1+x
2
2
2
2 4
2
32
x=0
In alternativa, si poteva usare il cambiamento di variabile t = arctan x e trovare
Z
0
1
1
arctan x dx =
1 + x2
Z
π
4
t dt = · · · =
0
π2
.
32
e quindi
1.5. Determinare l’integrale generale della seguente equazione differenziale
y 0 = xy 2
Svolgimento:
Si tratta di un’equazione a variabili separabili. Le soluzioni costanti sono quelle tali che y 2 = 0, cioè y = 0. Le soluzioni
non costanti verificano tutte y(x) 6= 0 per ogni x. Le soluzioni non costanti verificano quindi
y0
=x
y2
2
2
. La funzione − x2 +2C
è
e quindi − y1 = 21 x2 + C dove C è un reale indipendente da x. Abbiamo quindi y = − x2 +2C
√
definita su R se C > 0 e su R\{± −2C} se C 6 0 e quindi l’integrale generale dell’equazione è costituito
2
per C > 0 (definite su R);
• dalle funzioni − x2 +2C
√
√
√
√
2
• dalle funzioni − x2 +2C per C 6 0 (definite su (−∞; − −2C), (− −2C; −2C) e ( −2C; +∞));
• della funzione costante uguale a 0 (definita su R).
1.6. Risolvere il seguente problema di Cauchy
00
y + 2y 0 + y = 0
y(0) = 1
0
y (0) = 2
Svolgimento:
Si tratta di un’equazione differenziale del secondo ordine lineare a coefficienti costanti e omogenea. La sua equazione
caratteristica è
λ2 + 2λ + 1 = 0.
Ha una soluzione doppia λ = −1 per cui l’integrale generale dell’equazione è y(t) = Ae−t + Bte−t con A e B costanti.
Per verificare le condizioni iniziali, dobbiamo avere A = 1 e, siccome y 0 (t) = −Ae−t + Be−t − Bte−t , anche −A + B = 2,
quindi B = 3. La soluzione dell’equazione è quindi y(t) = (1 + 3t)e−t .
2.1. Studiare la funzione
f (x) = arctan
2x − 1
2x + 1
e tracciarne un grafico approssimativo.
Dominio, segno, eventuale parità, limiti ai bordi del dominio ed eventuali asintoti, eventuali punti di
discontinuità:
1
1
La funzione arctan è definita su R mentre la funzione 2x−1
2x+1 è definita su R\{− 2 }, quindi il dominio di f è Df = R\{− 2 }.
Il segno di arctan t è quello di t, quindi f (x) ha il segno di 2x−1
2x+1 che ha il segno di (2x − 1)(2x + 1). Quindi f (x) è
positiva per x < − 21 e x > 12 e negativa per − 12 < x < 12 .
Il dominio di f non è simmetrico rispetto all’origine quindi f non può essere né pari né dispari.
2x−1
π
Abbiamo lim 2x−1
2x+1 = 1 e lim 2x+1 = 1. La funzione arctan è continua su R e quindi lim f (x) = lim f (x) = 4 .
x→+∞
x→−∞
x→+∞
x→−∞
Abbiamo
2x − 1
lim
= +∞
1 − 2x + 1
x→(− 2 )
e
lim arctan t =
t→+∞
π
2
e quindi
π
lim f (x) = .
1 −
2
x→(− 2 )
Nello stesso modo limx→(− 1 )+f (x) = − π2 .
2
Le due funzioni arctan e
2x−1
2x+1
sono continue quindi f è continua.
Derivata prima ed eventuali punti di non derivabilità:
Le due funzioni arctan e
2x−1
2x+1
sono derivabili quindi f è derivabile su Df . La sua derivata è
f 0 (x) =
2(2x + 1) − 2(2x − 1)
(2x + 1)2
1
1+
2x−1
2x+1
2
4x + 2 − 4x + 2
(2x + 1)2 + (2x − 1)2
4
2
= 2
= 2
4x + 4x + 1 + 4x2 − 4x + 1
4x + 1
=
Nonostante l’espressione della derivata abbia senso in − 12 , la funzione f non è derivabile in − 12 (perché non vi è definita
e non si può neanché prolungarla per continuità perché i due limiti destro e sinitro di f in − 12 sono diversi).
Crescere e decrescere, massimi, minimi:
La derivata di f è ovviamente positiva su tutto Df . Quindi f è crescente su −∞; − 21 e su − 12 ; +∞ .
Attenzione:
non è crescente su Df .
La funzione f non ha nessun estremo locale perché ogni x di Df è incluso in un intervallo della forma (a; b) con
(a; b) ⊂ Df (per x < − 12 possiamo prendere a = 2x e b = − 21 e per x > − 21 possiamo prendere a = − 12 e b = 2x).
Quindi, secondo il teorema di Fermat, per avere un estremo locale in x dovremmo avere f 0 (x) = 0 e ciò non accade.
Siccome non ha nessun estremo locale, non ha nessun estremo globale.
Derivata seconda
La funzione f 0 (x) è derivabile su Df , quindi f ammette derivata seconda su Df . Abbiamo
f 00 (x) = −
2.4.2x
16x
=−
(4x2 + 1)2
(4x2 + 1)2
Concavità e convessità
La derivata seconda di f è positiva per x < 0 e negativa per x > 0 quindi f è convessa per x < 0 (e x 6= − 12 ) e concava
per x > 0 con un flesso in x = 0.
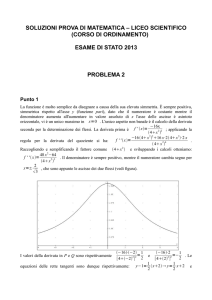
Grafico:
2
arctan 2x−1
2x+1
1.5
1
0.5
0
-0.5
-1
-1.5
-2
-3
-2
-1
0
1
2
2.2. Risolvere il seguente problema di Cauchy
y 0 = (log t)2 (cos y)2
y(1) = π4 .
Svolgimento:
L’equazione differenziale y 0 = (log t)2 (cos y)2 è un’equazione a variabili separabili. Le soluzioni costanti sono quelle per
le quali (cos y)2 = 0 cioè cos y = 0 cioè y = π2 + kπ per k ∈ Z. Per nessun k ∈ Z vale π4 = π2 + kπ per cui la soluzione
del problema di Cauchy non è costante.
Le soluzioni non costanti dell’equazione differenziale verificano cos y(t) 6= 0 per ogni t e quindi
y0
= (log t)2
cos2 y
Una primitiva di
Z
2
y0
cos2 y
2
è tan y mentre per calcolare una primitiva di (log t)2 facciamo due integrazioni per parti:
Z
(log t) dt = t(log t) −
1
t2 log t dt = t(log t)2 −2
t
Z
Z
2
log t dt = t(log t) −2t log t+2
dt = t(log t)2 −2t log t+2t+C.
Abbiamo quindi tan y = t(log t)2 − 2t log t + 2t + C per C costante reale. In t = 1, troviamo tan π4 = 2 + C e quindi
C = −1. Troviamo quindi
y(t) = arctan(t(log t)2 − 2t log t + 2t − 1).
La soluzione è definita su (0; +∞).
2.3. Stabilire il carattere della serie
∞
X
(n + 1)!
2(n2 )
n=1
Svolgimento:
Denotiamo un =
(n+1)!
2n2
il termine generale della serie. Abbiamo
un+1
=
un
(n+2)!
2(n+1)2
(n+1)!
2n2
2
(n + 2)! 2n
=
(n + 1)! 2(n+1)2
= (n + 2)2n
2
−(n+1)2
= (n + 2)2−2n−1
2
2
= (n + 2)2n −n −2n−1
1n+2
1n+2
=
=
2 22n
2 4n
Il limite di questa successione è 0 perché 4n è un infinito di ordine maggiore di n + 2 e quindi la serie è convergente.