Problema 2 - web

SOLUZIONI PROVA DI MATEMATICA – LICEO SCIENTIFICO
(CORSO DI ORDINAMENTO)
ESAME DI STATO 2013
PROBLEMA 2
Punto 1
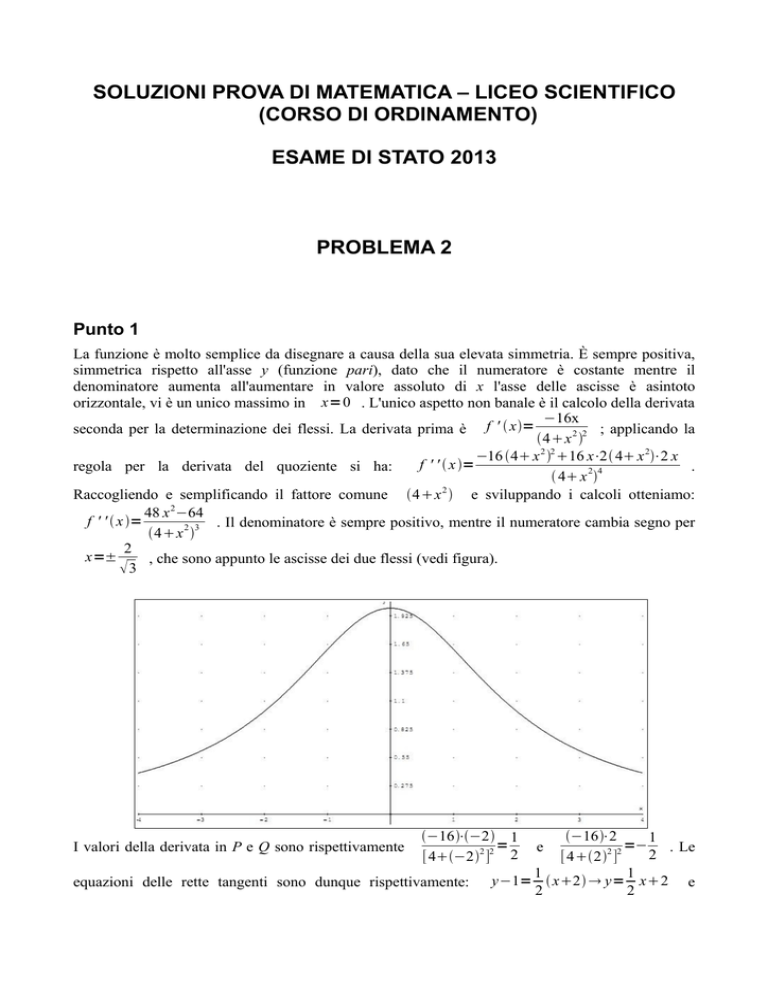
La funzione è molto semplice da disegnare a causa della sua elevata simmetria. È sempre positiva,
simmetrica rispetto all'asse y (funzione pari), dato che il numeratore è costante mentre il
denominatore aumenta all'aumentare in valore assoluto di x l'asse delle ascisse è asintoto
orizzontale, vi è un unico massimo in x=0 . L'unico aspetto non banale è il calcolo della derivata
−16x
seconda per la determinazione dei flessi. La derivata prima è f '  x=
; applicando la
4x 2 2
−16 4 x 2 2 16 x⋅2 4 x 2⋅2 x
f ' '  x =
regola per la derivata del quoziente si ha:
.
 4 x 24
Raccogliendo e semplificando il fattore comune 4x 2  e sviluppando i calcoli otteniamo:
48 x 2−64
f ' '  x =
. Il denominatore è sempre positivo, mentre il numeratore cambia segno per
2 3
4x 
2
x=±
, che sono appunto le ascisse dei due flessi (vedi figura).
3
I valori della derivata in P e Q sono rispettivamente
−16⋅−2 1
=
[4−22 ]2 2
equazioni delle rette tangenti sono dunque rispettivamente:
−16⋅2
1
=− . Le
2 2
2
[42 ]
1
1
y−1=  x2  y= x2 e
2
2
e
1
1
y−1=−  x −2 y=− x2 . Le due rette si incontrano nel punto K di coordinate
2
2
Verifichiamo che il quadrilatero così ottenuto è effettivamente un rombo:
OP=OQ = 22 12= 5 ;
0, 2 .
KP=KQ=  222−12 = 5 .
Per calcolare gli angoli del rombo, consideriamo ad esempio il triangolo isoscele OPK e
dividiamolo in due triangoli rettangoli uguali mediante l'altezza PH. Detto α l'angolo 
OPH
1
possiamo applicare la definizione di seno di un angolo per ottenere sin =
. Utilizzando una
5
calcolatrice troviamo che =26,56505 gradi. Ora, 0,56505 gradi è una frazione di grado
pari a 0,56505⋅60=33,903 primi, e 0,903 primi è una frazione di primo pari a
0,903⋅60≃54 secondi. Abbiamo quindi =26o 33' 54 ' ' . Per trovare la misura degli angoli
acuti del rombo dobbiamo raddoppiare  : 2⋅54' ' =108 ' ' =60 ' ' 48 ' ' =1' 48 ' ' , mentre
o
o
2⋅34 '=68 '=60 '8 ' =1 8' , cosicché 2 =53 8 ' 48 ' ' è la misura dei due angoli acuti del
rombo, mentre gli angoli ottusi sono semplicemente i supplementari di questi:
o
o
o
179 59' 60 ' ' −53 8' 48 ' ' =126 51' 12 ' '
Punto 2
Scriviamo l'equazione della circonferenza  : x 2 y−12=1  x 2 y 2−2y=0 , mentre la
generica retta t passante per l'origine ha equazione y=mx . Mettiamo a sistema t con  ,
ottenendo l'equazione: x 2 1m2 −2 mx=0 . Raccogliendo la x troviamo due soluzioni: una è
m
banalmente x=0 , mentre l'altra – che corrisponde al punto A – è x=
2 . La y di A sarà
1m
2 m2
quindi: y A=
.Adesso andiamo a calcolare le intersezioni della retta t con la retta di
1m2 
2
equazione y=2 . La soluzione del sistema ci dà per l'ascissa di B l'espressione x B=
. Se
m
2
adesso vogliamo eliminare il parametro m tra le due espressioni, si deve sostituire m=
in
x
4
2⋅ 2
2
2m
x
8
y=
=
f x .
, ottenendo y=
2
2 , che è proprio l'equazione di
4
1m 
1 2 4 x
x
Punto 3
2
Si tratta di calcolare l'integrale definito:
∫  48 x 2  dx
. Calcoliamo la primitiva:
0
8
∫  4 x 2  dx=∫
4
2
x
1 
4
x
d 
2
Possiamo quindi operare la sostituzione
y=
x
2
con
dy
x
x
=4 arctan  yC =4 arctan  C .
dy=d   e riportarci all'integrale elementare 4 ∫
2
2
2
1 y
2
Abbiamo quindi
∫  48 x 2  dx=4⋅[arctan 1−arctan  0]=4⋅4 =
. Ma questa è proprio l'area
0
del cerchio  di raggio 1, essendo l'area del cerchio di raggio r data da  r 2 .
Per calcolare l'area sottesa da tutta la curva sarà necessario ricorrere ad un integrale improprio. A
causa della simmetria di f  x  potremo calcolare l'integrale tra zero e l'infinito e poi raddoppiare
K
8
dx . Come abbiamo visto la primitiva della
il risultato. Dovremo quindi valutare il lim ∫
2
K  ∞ 0 4 x
x
funzione è 4 arctan  C , cosicché l'integrale improprio si riduce al calcolo del limite:
2
K
lim 4 arctan  =2  . Ma questa è l'area sottesa da metà curva, l'area compresa tra tutta la
2
K ∞
curva e l'asse delle ascisse sarà quindi 4  , cioè quattro volte l'area del cerchio di raggio 1.
Punto 4
Dato che viene chiesto il volume di un solido ottenuto dalla rotazione intorno all'asse y, per poter
applicare il teorema di Pappo-Guldino, dobbiamo esplicitare la funzione in termini di x. Osserviamo
che si otterranno due rami, uno per le x positive e uno per quelle negative; noi ne prenderemo solo
8
8
uno. Abbiamo quindi y 4x 2 =8  x 2 = −4  x=
−4 . L'area di ogni sezione del solido di
y
y
8
rotazione con un piano perpendicolare all'asse delle y è un cerchio di raggio x=
−4 , la cui
y
8
area sarà quindi  −4 . Applicando il principio di Cavalieri calcoliamo allora il volume
y
2
8
richiesto per mezzo dell'integrale: ∫  −4 dy .
y
0

