CORSO DI FISICA II
16 Luglio 2014
Prima Prova Scritta
1) Si consideri una regione dello spazio posta tra due piani conduttori paralleli, distanti d, e tenuti a
potenziale nullo. Nella regione è presente una densità di carica che dipende dalla coordinata x
secondo la relazione ρ = ρ0 . cos ( πx/d).
a) Si determini il campo elettrico nella regione tra i due piani
b) Si calcoli il valore massimo del potenziale.
c) Si calcoli il periodo delle piccole oscillazioni di un elettrone attorno a un punto in cui si ha il
massimo del potenziale.
Sia ρ0 = 7 nC/m3, d = 20 cm, me = 9.1.10-31 kg, qe = -1.6.10-19 C, 0 =8.854·10-12 F m-1
(x)
x
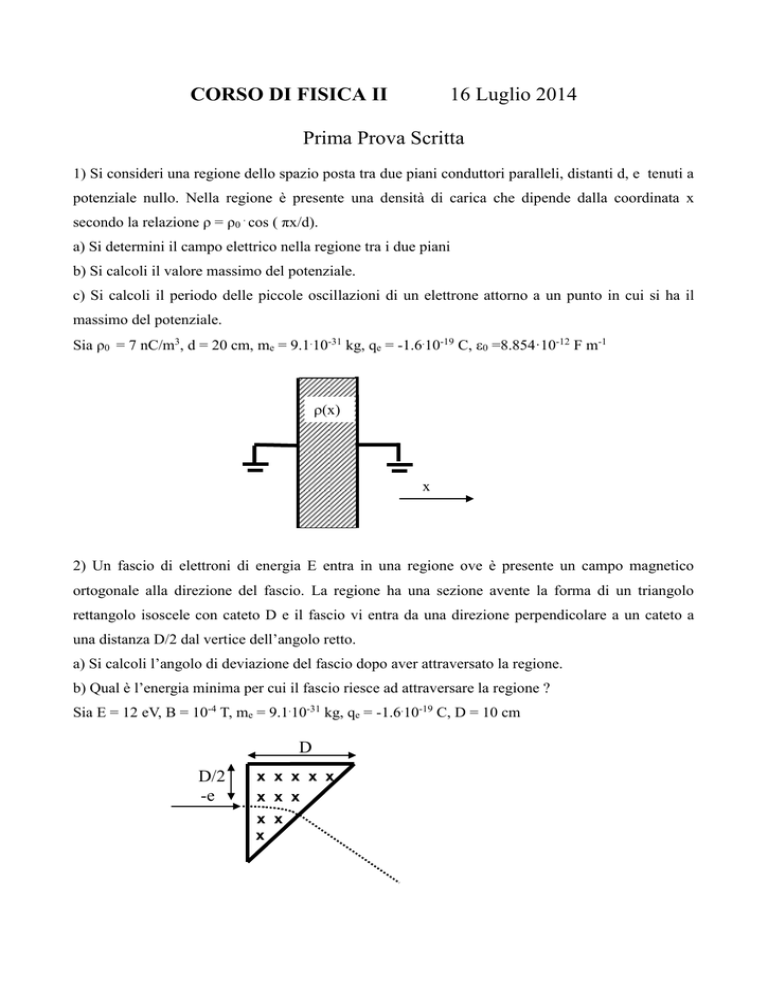
2) Un fascio di elettroni di energia E entra in una regione ove è presente un campo magnetico
ortogonale alla direzione del fascio. La regione ha una sezione avente la forma di un triangolo
rettangolo isoscele con cateto D e il fascio vi entra da una direzione perpendicolare a un cateto a
una distanza D/2 dal vertice dell’angolo retto.
a) Si calcoli l’angolo di deviazione del fascio dopo aver attraversato la regione.
b) Qual è l’energia minima per cui il fascio riesce ad attraversare la regione ?
Sia E = 12 eV, B = 10-4 T, me = 9.1.10-31 kg, qe = -1.6.10-19 C, D = 10 cm
D
D/2
-e
x x x x x
x x x
x x
x
CORSO DI FISICA II
16 Luglio 2014
Seconda Prova Scritta
1) Un condensatore a facce piane parallele è costituito da due elettrodi circolari di raggio R.
Sull’elettrodo inferiore è posto un cilindro costituito da un materiale isolante di costante dielettrica
relativa r di altezza H e raggio uguale a quello degli elettrodi. L’elettrodo superiore è appeso a una
molla con costante elastica K e lunghezza a riposo L. In questa configurazione la distanza tra gli
elettrodi è pari a 2H. Se il condensatore viene collegato a un generatore di f.e.m. costante V,
a) si determini la posizione di equilibrio dell’elettrodo superiore.
b) Si calcoli l’energia elettrostatica del condensatore in tale posizione.
Sia V = 100 V, R = 7 cm, H = 2 mm, r = 2, 0 =8.854·10-12 F m-1, L = 1 cm, k = 5·10-1 N/m
k
H
H
2) Una spira quadrata di lato L e resistenza R viene fatta passare a velocità uniforme V attraverso un
solenoide costituito da un numero N di spire circolari avvolte lungo un cilindro di altezza H,
supposta indefinita. Il diametro delle spire è pari a L e in ciascuna scorre in verso antiorario una
corrente stazionaria I.
a) Si determini la corrente indotta nella spira durante il passaggio attraverso il solenoide.
b) Si calcoli in quale momento essa è massima
Sia L = 20 cm, V = 2 m/s, N = 100, H =80 cm, I = 5 A, R= 5 Ω , μ0 = 4π · 10-7 H m-1
Vista in sezione
v
v
I
B