Derivata Prima - vincenzoscudero.it

appunti di analisi
vincenzo scudero
DERIVATA PRIMA DI UNA FUNZIONE IN UN PUNTO
Sia data la funzione y=f(x) definita in un insieme D e sia
Consideriamo il punto
x 0 un punto appartenente ad D.
x 0+h , dove h rappresenta un incremento della variabile indipendente x
(l'incremento può anche essere negativo). In corrispondenza di x 0 e di x 0+h consideriamo i
valori che assume la funzione, f (x 0) e f ( x 0+h) .
y
f(x0+h)
Q
Δy
f(x0)
P
R
Δx
x0
O
x0+h
x
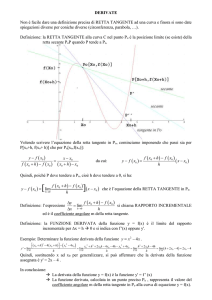
Sul grafico della funzione si possono considerare i due punti P e Q aventi per coordinate cartesiane
rispettivamente
P[ x 0 ; f ( x 0)] e Q[ x 0+h ; f (x 0+h)]
La quantità Δ x =(x 0+h)−( x 0 )=h è detta incremento della variabile indipendente
La quantità Δ f =f (x 0+h)−f (x 0) è detta incremento della variabile indipendente
(nella figura Δ x =PR e Δ f =QR )
La quantità
Δ f f ( x 0+h)−f ( x0 )
=
è detta rapporto incrementale.
Δx
h
www.vincenzoscudero.it
appunti di analisi
vincenzo scudero
Mentre l'incremento
Δ f misura la variazione di “quota” di f(x) nel tratto
Δ x =( x 0+h)−(x 0 ) ,
il rapporto incrementale misura il rapporto tra i due incrementi, cioè la pendenza del segmento che
unisce i due punti sul grafico P e Q. Questo rapporto è un numero reale che corrisponde al
coefficiente angolare della retta passante per i punti P e Q (retta secante il grafico nei punti P e Q).
Conoscendo le proprietà del coefficiente angolare di una retta è possibile notare che se il rapporto
incrementale è positivo allora il grafico avrà un andamento crescente (pendenza positiva), se il
rapporto incrementale è negativo allora il grafico avrà un andamento decrescente (pendenza
negativa) e se il rapporto incrementale è uguale a zero l'andamento della funzione sarà costante.
Utilizzando il concetto di limite passiamo adesso a definire la derivata prima in un punto.
Se, infatti, facciamo tendere a zero l'incremento h, se, cioè, il punto
anche il valore
f ( x 0+h) si avvicina al valore
x 0+h si avvicina a
x0 ,
f (x 0) . Sul grafico della funzione ciò significa
che il punto Q tende verso il punto P e la retta secante il grafico in P e Q tende ad assumere la
posizione della retta tangente al grafico in P.
Δ f f ( x 0+h)−f ( x 0 )
, esso, al tendere di h a zero,
=
Δx
h
Se consideriamo il rapporto incrementale
assume la forma indeterminata
0
. Ciò significa che il limite del rapporto incrementale, al
0
tendere di h a zero, dà come risultato, generalmente, una forma indeterminata. Se tale forma si
risolve in un valore reale finito allora potremo dire che tale valore è la derivata prima della funzione
nel punto
x 0 . Geometricamente rappresenta il coefficiente angolare della retta tangente al grafico
nel punto
P[ x 0 ; f (x 0)] . Più precisamente:
definizione
Data la funzione y=f(x) e un punto
f ( x) nel punto
incrementale
x 0 appartenente al suo dominio, si dice derivata prima di
x 0 , e si indica con
f ' (x 0) , il limite, se esiste ed è finito, del rapporto
Δ f f ( x 0+h)−f (x 0 )
al tendere di h verso 0.
=
Δx
h
f ' (x 0)=lim
h→0
f (x 0 +h)−f ( x 0)
=l∈ R
h
www.vincenzoscudero.it
appunti di analisi
vincenzo scudero
y
P
m=tg(α)=f'(x0)
α
f(x0)
x
x0
O
Equazione della retta tangente al grafico di una funzione in un punto
La derivata prima di una funzione in un punto è, quindi, un valore numerico, e coincide con il
coefficiente angolare della retta tangente al grafico della funzione nel punto di ascissa
x 0 . In
particolare, ricordando la formula che permette di determinare l'equazione della retta passante per
un punto con coefficiente angolare m noto
y− y 0 =m(x−x 0)
essendo
m=f ' (x 0) , possiamo determinare l'equazione della retta tangente al grafico della
funzione
y=f ( x ) nel punto
P[ x 0 ; f ( x 0)]
y−f (x 0 )=f ' ( x 0)( x−x 0 )
FUNZIONE DERIVATA PRIMA
Supponiamo che per la funzione
y=f (x ) sia possibile calcolare la derivata prima in ogni punto
del suo dominio D (geometricamente significa che in ogni punto del grafico esiste la retta tangente
al grafico della funzione), cioè che per ogni
x∈D esista
f ' (x) . In tal caso è possibile
associare ad ogni valore x del dominio uno ed un solo numero reale
f ' (x) (ricordiamo che la
derivata prima in un punto è il risultato del calcolo di un limite che, se esiste, è unico in virtù del
teorema dell'unicità del limite).
www.vincenzoscudero.it
appunti di analisi
vincenzo scudero
La funzione che ad ogni
x∈D associa la derivata prima in x ,
f ' (x) , si chiama funzione
derivata prima di f (x) e si indica con uno dei seguenti simboli
y'
f ' (x)
df
dx
D[f (x )]
Esempio
Determinare la (funzione) derivata prima della funzione
tale funzione nel punto
y=x
2
, calcolare la derivata prima di
x=3 e determinare l'equazione della retta tangente al grafico della
funzione nel punto di ascissa 3.
Per prima cosa scriviamo il rapporto incrementale
2
2
Δ f f ( x+h)−f ( x ) (x+h) −x x 2+2hx+h2−x 2 h(2x+h)
=
=
=
=
=2x+h
Δx
h
h
h
h
passando al limite, al tendere di h verso 0, otteniamo la funzione derivata prima f ' ( x)
f ' (x)=lim
h→0
La derivata prima della funzione
Δf
=lim (2x+h)=2x
Δ x h→0
y=x 2 è, dunque, la funzione
y '=2x .
Il valore della derivata prima in x=3 è:
f ' (x) x=3 =f '( 3)=2⋅(3)=6
La derivata prima in
x=3 rappresenta il coefficiente angolare della retta tangente che dobbiamo
determinare. Per conoscere sua equazione dobbiamo conoscere anche il valore della funzione in
x=3 :
2
f (3)=(3) =9
L'equazione della retta tangente è:
y−f (x 0 )=f ' ( x 0)( x−x 0 )
y−f (3)=f '(3)(x−3)
y−9=6 (x−3)
y=6x−18+9=6x−9
www.vincenzoscudero.it