derivate - Share Dschola

DERIVATE
Non è facile dare una definizione precisa di RETTA TANGENTE ad una curva e finora si sono date
spiegazioni diverse per coniche diverse (circonferenza, parabola, …).
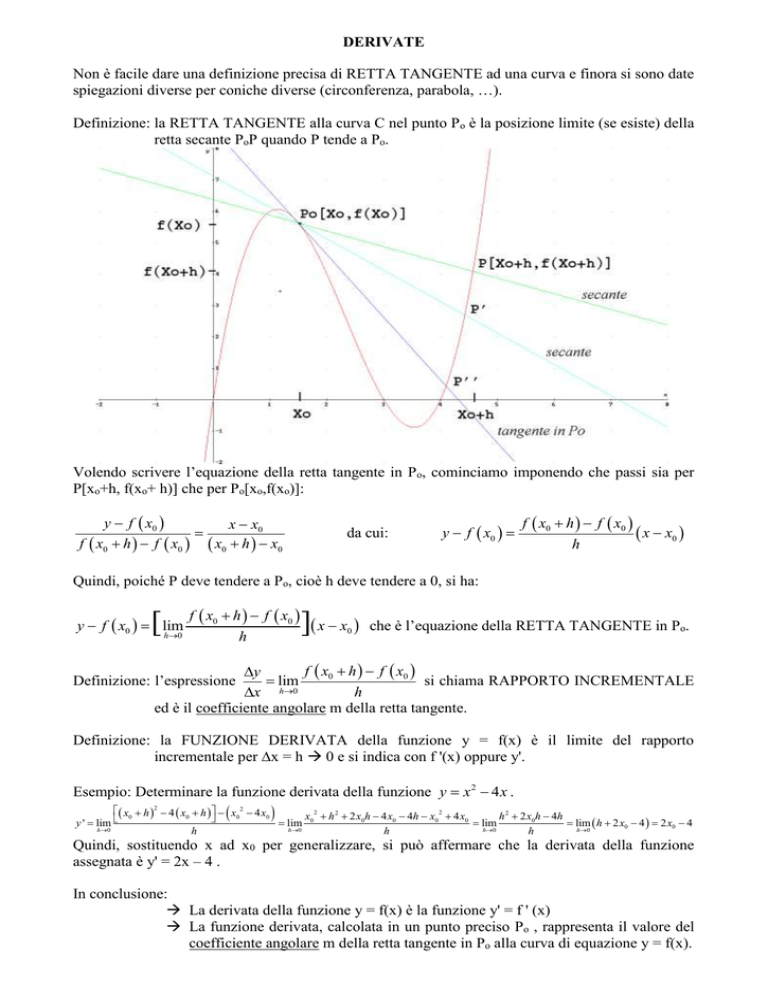
Definizione: la RETTA TANGENTE alla curva C nel punto Po è la posizione limite (se esiste) della
retta secante PoP quando P tende a Po.
Volendo scrivere l’equazione della retta tangente in Po, cominciamo imponendo che passi sia per
P[xo+h, f(xo+ h)] che per Po[xo,f(xo)]:
y  f  x0 
x  x0

f  x0  h   f  x0   x0  h   x0
da cui:
y  f  x0  
f  x0  h   f  x0 
 x  x0 
h
Quindi, poiché P deve tendere a Po, cioè h deve tendere a 0, si ha:
[
y  f  x0   lim
h0
f  x0  h   f  x0 
h
] x  x 
0
che è l’equazione della RETTA TANGENTE in Po.
f  x0  h   f  x0 
y
 lim
si chiama RAPPORTO INCREMENTALE
h

0
x
h
ed è il coefficiente angolare m della retta tangente.
Definizione: l’espressione
Definizione: la FUNZIONE DERIVATA della funzione y = f(x) è il limite del rapporto
incrementale per ∆x = h  0 e si indica con f '(x) oppure y'.
Esempio: Determinare la funzione derivata della funzione y  x 2  4 x .


 x0  h 2  4  x0  h   x0 2  4 x0
2
2
x  h 2  2 x0h  4 x0  4h  x0  4 x0
h 2  2 x0 h  4 h

y '  lim 
 lim 0
 lim
 lim  h  2 x0  4   2 x0  4
h 0
h 0
h 0
h 0
h
h
h
Quindi, sostituendo x ad x0 per generalizzare, si può affermare che la derivata della funzione
assegnata è y' = 2x – 4 .
In conclusione:
 La derivata della funzione y = f(x) è la funzione y' = f ' (x)
 La funzione derivata, calcolata in un punto preciso Po , rappresenta il valore del
coefficiente angolare m della retta tangente in Po alla curva di equazione y = f(x).
DERIVATE
Il concetto di DERIVATA è uno dei più importanti della Matematica, sia pura che applicata.
L’idea di base è quella di misurare gli INCREMENTI delle grandezze; infatti spesso nello studio di
un fenomeno sono più significativi i dati sulla VARIAZIONE di una grandezza piuttosto che quelli
sulla grandezza stessa (peso durante dieta, valore dell’inflazione in un dato periodo, ...)
Esempio
Consideriamo il capitale C investito in un’operazione finanziaria e valutiamo la sua REDDITIVITÀ
nell’istante to:
 a partire da tale istante lasciamo trascorrere un intervallo h (l’istante successivo su cui noi
fisseremo l’attenzione sarà quindi to+h)
 misuriamo la VARIAZIONE del capitale a partire dall’istante to fino all’istante to+h,
indicandola con C(to+h) – C(to)
 determiniamo la redditività media
C  t0  h   C  t0  C  t0  h   C  t 0 

h
 t0  h   t 0
C  t0  h   C  t 0 
h 0
h
 quando l’intervallo di tempo tende a zero, la redditività istantanea è lim
 tale limite, se esiste ed è finito, si chiama DERIVATA DELLA FUNZIONE CAPITALE C.
Passando al caso generale, sia y = f(x) una funzione definita in un intervallo [a,b] e sia xo un punto
interno a questo intervallo; se da xo si passa ad un altro punto xo+h dell’intervallo [a,b] si dice che si
è dato alla variabile x un incremento (positivo o negativo) h.
La differenza f(xo+ h) – f(xo) si chiama INCREMENTO della funzione f e può essere positivo,
negativo o nullo.
Infine, il rapporto
f  x0  h   f  x0 
si dice RAPPORTO INCREMENTALE della funzione f;
h
questo rapporto, una volta fissato xo , varia al variare di h.
DEFINIZIONE: si chiama DERIVATA DELLA FUNZIONE f(x) nel punto x o il limite, se esiste ed
è finito, del rapporto incrementale al tendere a zero dell’incremento h; cioè:
lim
h 0
f  x0  h   f  x0 
h
La derivata di f(x) nel punto xo è un numero, mentre la derivata della funzione f(x) in un generico
punto x si indica con f '(x) oppure y' ed è una funzione.
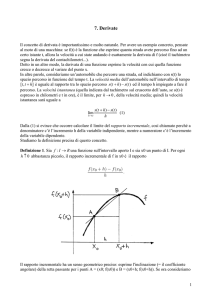
Esiste anche una importante INTERPRETAZIONE GEOMETRICA DELLA DERIVATA che è la
seguente:
Il valore della derivata f '(x) in un dato punto xo è uguale al COEFFICIENTE ANGOLARE m della
retta tangente alla curva di equazione f(x) nel punto Po[xo,f(xo)]; quindi y  f  x0   f '( x0 )   x  x0 