Calcolo di derivate con il limite del rapporto incrementale

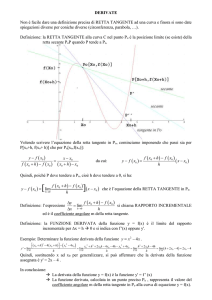
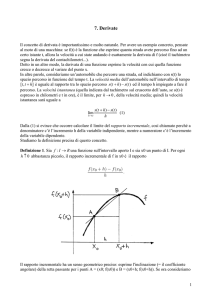
Calcolo di derivate con il limite del rapporto incrementale
Premessa
Ricordiamo che assegnata la funzione reale di variabile reale f : A  R , con A  R , se x0 è un
punto del dominio e di accumulazione per esso, in simboli x0  A  x0  Dr  A , si dice che la
funzione f è derivabile in x0 se e solo se esiste ed è finito il valore del limite del rapporto
incrementale
f ( x)  f ( x0 )
f
,

x
x  x0
per x  x0 . Se x0 il punto è di accumulazione solo a sinistra o solo a destra, il limite del rapporto
andrà studiato solo da quel lato. Il limite del rapporto incrementale è
f ( x)  f ( x0 )
.
(1)
x  x0
x  x0
Il limite del rapporto incrementale si può porre anche in una delle seguenti forme equivalenti:
f ( x0  h)  f ( x0 )
f ( x0  x)  f ( x0 )
,
(2)
lim
lim
h 0
x 0
h
x
La scelta di una delle tre forme del rapporto incrementale è ininfluente ai fini del risultato; tuttavia,
a livello di calcolo algebrico, le difficoltà che si incontrano con una forma possono essere più
complesse di quelle incontrate con le altre. L’esperienza suggerirà la scelta da adottare.
lim
Esercizi svolti
Applicando la definizione di derivata, determinare il valore della derivata prima delle funzioni di
seguito indicate, ciascuna nel punto xo assegnato.
a)
nel punto xo=1
R.: f '(1)  0 .
f ( x)  x 2  2 x
b)
1
R.: f '(3)  .
f ( x)  x  2 , nel punto x0  3
2
c)
x2
11
f ( x) 
, nel punto x0  1
R.: f '(1) 
x 5
36
d)
x2
Calcolare la derivata prima della funzione f ( x) 
nel generico punto x0 del suo dominio che
x 5
x0 2  10 x0
è R  5 .
R.: f '( x0 ) 
2
 x0  5
e)
f ( x)   x  1 x  1 , nei punti x0  1 , x1  1 .
R.: La funzione non è derivabile nel punto x=-1, mentre f '(1)  2
.
f)
Luigi Lecci: www.matematicaescuola.it
Pagina 1
Determinare il valore della derivata prima della
funzione f ( x)  xsenx nel punto x0 

e l’equazione
2
della retta tangente al diagramma nel punto (x0;f(x0)).
  
 
R.: f '    1 , la retta tangente in A  ;  è y=x.
2
2 2
g)
Determinare la derivata prima della funzione f ( x)  xsenx nel generico punto x0.
R.: f '( x0 )  senx0  x0 cos x0 .
h)
Per la funzione f ( x)  xe x , calcolare la derivata prima nel generico punto x0 e successivamente nel
punto x0  1 .
R.: f '( x0 )  x0e x0  e x0 ; f '(1)  0
Luigi Lecci: www.matematicaescuola.it
Pagina 2