Pagina 199 n. 95, n.94, n87, n91
Pagina 199 n. 95
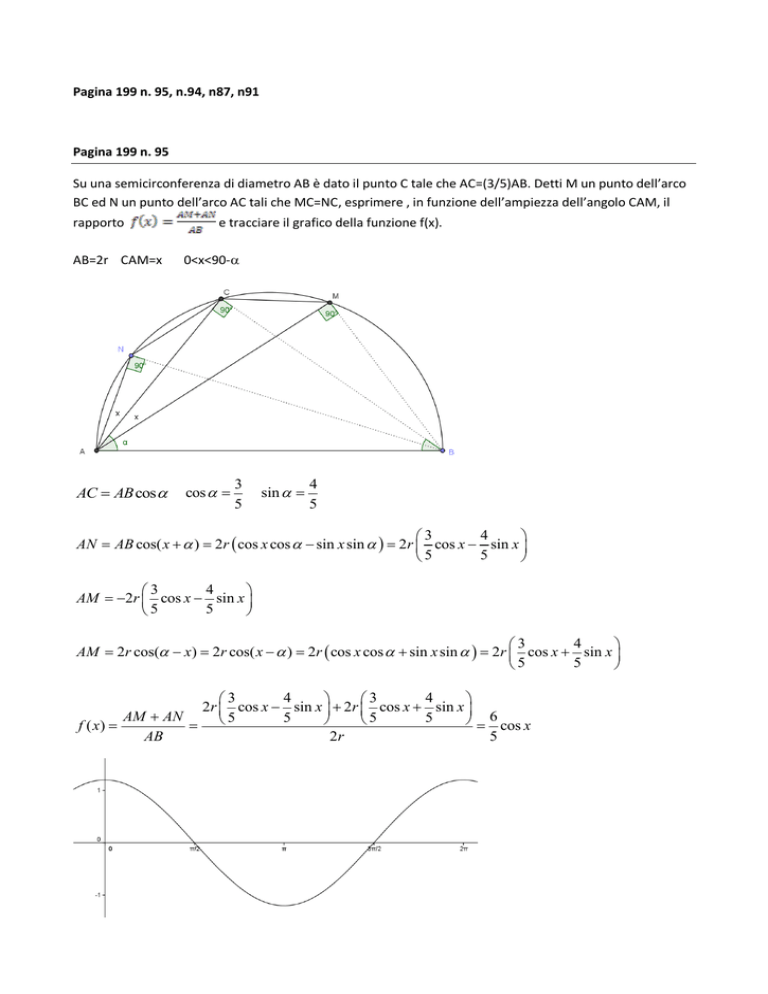
Su una semicirconferenza di diametro AB è dato il punto C tale che AC=(3/5)AB. Detti M un punto dell’arco
BC ed N un punto dell’arco AC tali che MC=NC, esprimere , in funzione dell’ampiezza dell’angolo CAM, il
rapporto
e tracciare il grafico della funzione f(x).
AB=2r CAM=x
0<x<90-
AC AB cos
cos
3
5
sin
4
5
4
3
AN AB cos( x ) 2r cos x cos sin x sin 2r cos x sin x
5
5
4
3
AM 2r cos x sin x
5
5
4
3
AM 2r cos( x) 2r cos( x ) 2r cos x cos sin x sin 2r cos x sin x
5
5
4
4
3
3
2r cos x sin x 2r cos x sin x
AM AN
5
5
5
5
6 cos x
f ( x)
AB
2r
5
Problema n. 94
Sia AC=r
una corda di una circonferenza di centro O e diametro AB=2r. Sul minore degli archi CB
considerare un punto P, Porre BAP=x e tracciare il grafico della funzione f(x)=2PH + AH essendo PH la
distanza di P dalla tangente in A alla circonferenza e determinare il massimo.
Dato che la corda AC=r
AC=r
Sia PAB=x
, considerando il diametro AB e il triangolo rettangolo ACB. Abbiamo che
da cui
=
e quindi CAB==30°
0<x<30°.
Determiniamo PA , e consideriamo il triangolo APB. PA AB cos x 2r cos x
PH=AK=PA cosx=2r cos2x,
PK=AH=PAsinx=2rsinxcosx
f ( x) 2 PH AH 4r cos 2 x 2r sin x cos x 4r
1 cos 2 x
r sin 2 x
2
f ( x) r (2 2cos 2 x sin 2 x)
vedendo gli appunti in cui su sito moltiplichiamo e dividiamo per
2
1
sin 2 x
cos 2 x
a2 b2 12 22 5 sin 2 x 2cos 2 x 5
5
5
sin 2x 2cos 2 x 5 cos sin 2 x sin cos 2 x 5 sin 2 x dove cos
Massimo per 2 x
2
x
4
2
1
2
e sin
5
5
Problema n. 87
In un triangolo ABC l’altezza CH relativa alla base AB è lunga 2°. Considerati il punto medio D di CH e le sue
proiezioni E e F sui lati AC e CB , indicata con 2x l’ampiezza dell’angolo ACB, si tracci il grafico della funzione
f(x)= perimetro(CFDE). Per quale valore di x la funzione assume perimetro massimo=? Per quale valore di x
2 2a
il perimetro è pari a
6a
.e
0<2x<180 0<x<90
CE CF a cos x ED DF a sin x
1
1
P(CEFD) 2a sin x 2a cos x 2a 2
sin x
cos x 2a 2 cos 45sin x sin 45cos x
2
2
P (CEFD ) 2a 2 sin( x 45)
1) Massimo per x+45=90 da cui x=45
P (CEFD ) 2a sin x 2a cos x a 2 2
2)
sin x cos x 2
.
sin 2 x cos2 x 2sin x cos x 2 2sin x cos x 1 sin 2 x 1 2x 90 x 45
P (CEFD) 2a sin x 2a cos x a 6 2sin x 2cos x 6
3) .
4sin 2 x 4cos 2 x 8sin x cos x 6
4sin 2 x 4cos2 x 8sin x cos x 6sin 2 x 6cos2 x 2sin 2 x 8sin x cos x 2cos 2 x 0
tan 2 x 4 tan x 1 0 tan x 2 4 1 2 3
x 75 x 15
Problema n. 91
AC r 3
Sia
una corda della semicirconferenza di diametro AB=2r.
a) Condurre una retta perpendicolare ad AB che incontri la corda AC in Q e l’arco AC in P e studiare la
funzione f(x)=PQ essendo BAP=x e tracciare il grafico
b) Determinare il valore massimo di PQ
PQ
c) Determinare il valore di x per
AC r 3 2r cos cos
AP 2r cos x
3r
3
3
CAB 30 PAB x
2
0<x<90
AH PA cos x 2r cos2 x
PH PAsin x 2r cos x sin x QH AH tan 30
PQ PH QH 2r cos x sin x
3
2r cos 2 x
3
3
2r cos 2 x
3
3 1 cos 2 x
3
3 r
3r
f ( x) r sin 2 x
2
cos 2 x
r sin 2 x
3sin 2 x 3 cos 2 x
3
2
3
3 3
3
f ( x)
r
3r
3sin 2 x 3 cos 2 x
3
3
a2 b2 9 2 12 2 3
dividendo e moltiplicando per
3
3
r
3
3r r
1
3r
f ( x) 2 3
sin 2 x
cos 2 x
2 3
sin 2 x cos 2 x
3
3
3
2
3
2 3
2 3
2
r
3r 2 3r
3r
f ( x) 2 3 cos 30sin 2 x sin 30 cos 2 x
sin 2 x 30
3
3
3
3
Massimo per 2x-30=90 2x=120 x=60°
PQ 2r cos x sin x
3
3
2r cos 2 x
r 6cos x sin x 2 3 cos 2 x 3
3
3
6cos x sin x 2 3 cos 2 x 3 cos 2 x 3 sin 2 x
3 tan 2 x 6 tan x 3 3 0 tan x
3 9 9
3
3
x=60°










