CAPITOLO III
La giunzione p-n
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-1
II.1 Formazione della giunzione
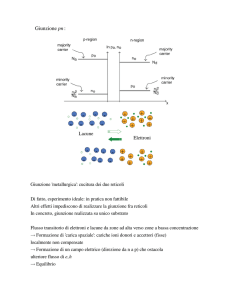
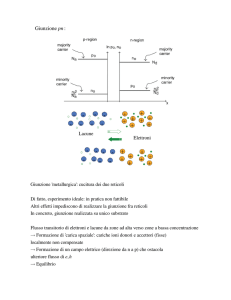
Se considero due materiali semiconduttori drogati uno di tipo “n” e l’altro di tipo “p” posso
schematizzarne le bande come in figura con i livelli di Fermi disposti nel modo visto nel capitolo I.
Quando unisco i materiali si avrà diffusione di portatori dovuta al gradiente di concentrazione.
Le lacune del materiale di tipo p in prossimità dell’interfaccia si muoveranno verso la regione drogata
n lasciando ionizzati gli atomi accettori originari e quindi una carica netta negativa. Allo stesso modo
gli elettroni degli atomi donori in prossimità dell’interfaccia si muoveranno verso la regione p
lasciando degli ioni positivi nella regione n.
Si avrà dunque la situazione illustrata in figura 2 dove a destra e sinistra della giunzione ci sarà una
carica netta rispettivamente negativa e positiva.
La regione corrispondente è chiamata regione di carica spaziale (o regione di svuotamento) ai capi
della quale dunque si manifesta un campo elettrico, il quale, raggiunta una condizione di equilibrio si
oppone all’ulteriore flusso di portatori.
Nella regione di carica spaziale ci sono dunque due correnti:
•
La corrente di diffusione dovuta al gradiente di concentrazione dei portatori
•
La corrente di deriva dovuta alla presenza del campo elettrico
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-2
Il diagramma a bande presenta due regioni: quella lontano dalla giunzione che si comporta come il
materiale isolato (detta regione quasi neutra) e quella in prossimità della giunzione (la regione di
svuotamento).
All’equilibrio termodinamico il livello di Fermi si mantiene costante su tutta la giunzione, anche
all’interfaccia tra i materiali e il flusso netto di corrente deve essere nullo sia per le lacune che per gli
elettroni:
dn
=0
dx
dp
J p = J pderiva + J pdiffusione = qµ p pε − qD p
=0
dx
J n = J nderiva + J ndiffusione = qµ n nε + qDn
( .1)
La distribuzione di carica spaziale e il potenziale elettrostatico sono dati dall’equazione di Poisson:
ρ
d 2ψ
dε
q
=−
= − s = − (N D − N A + p − n)
2
dx
εs
εs
dx
(III.2)
dove ρ s è la densità di carica spaziale, ε s la costante dielettrica relativa del semiconduttore, ND e NA la
densità dei donori ed accettori e p ed n la densità di lacune ed elettroni liberi.
L’equazione di Poisson è molto importante quando ho una variazione di concentrazione in funzione
della posizione.
Nella zona lontano dalla giunzione il potenziale è costante, le bande sono piatte e deve dunque essere
rispettata la neutralità di carica, cioè
d 2ψ
= 0 e quindi vale N D − N A + p − n = 0 .
dx 2
Nella zona p vale N D = n = 0 e p = N A che sostituite nella espressione
p = ni e
( Ei − EF )
kT
(vista nel
cap.I) porta a
kT ⋅ ln
NA
= ( Ei − EF ) . Quindi il potenziale può essere espresso come
ni
ψp =−
( Ei − EF )
kT N A
=−
ln
q
q
ni
Allo stesso modo per gli elettroni nella regione n
ψn = −
( Ei − EF ) kT N D
=
ln
q
q
ni
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-3
Quindi il potenziale intrinseco o di built-in della giunzione è la somma dei due contributi trovati:
Vbi = ψ n −ψ p =
N N
kT
⋅ ln A 2 D
q
ni
(III.3)
Esempio: Calcolare il potenziale di built-in di una giunzione p-n con NA=1018 cm-3 e ND=1015 cm-3 a
temperatura ambiente
Vbi =
⎛ 1018 ×1015 ⎞
N N
kT
⋅ ln A 2 D = 0.0259ln ⎜
= 0.755V
10 2 ⎟
q
ni
⎝ (1.45 ×10 ) ⎠
Se la giunzione è “brusca” la densità di carica spaziale è mostrata in figura
La regione di svuotamento è svuotata di portatori liberi. Si può usare l’equazione di Poisson anche in
questa regione dove vale
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-4
qN
d 2ψ qN A
d 2ψ
nella
regione
svuotata
p
e
=
= − D nella regione svuotata n. Integrando le due
2
2
dx
εs
dx
εs
equazioni si ottiene il campo elettrico che ha il massimo alla giunzione, cioè
"
N
$ −q A x + x p
con − x p < x < 0
εs
$
ε x =#
NA
ND
$
$ q ε x p -q ε x con 0 < x < xn
s
s
%
(
()
)
che è massimo per x=0:
εm
=
qN D
qN A
xn =
x
εs
εs p
(III.4)
Per avere neutralità di carica, la carica accumulata a sinistra della giunzione deve essere pari a quella
presente a destra cioè N A x p = N D xn , dove l’estensione della regione di carica spaziale si esprime
W = x p + xn . Integrando il campo elettrico su tutta la regione di carica spaziale si ottiene una nuova
espressione per il potenziale intrinseco della giunzione.
xn
Vbi = − ∫
− xp
2
A p
ε ( x)dx = qN2ε x
s
+
qN D xn2 1
= ε mW
2ε s
2
(III.5)
integrando il campo elettrico si ottiene l’espressione accurata dell’estensione della regione di carica
spaziale in una giunzione brusca
)
#
&
+ −q N A % 1 x 2 + x ⋅ x ( + C
con − x p < x < 0
p
1
εs $ 2
+
'
V x =*
&
ND # 1 2 NA
+
−q
x
−
x
⋅
x
con 0 < x < xn
%
(+C
+
ε s %$ 2
N D p (' 2
,
()
imponendo la condizioni al contorno V (−x p ) = 0
)
#
&
+ −q N A % 1 x 2 + x ⋅ x + 1 x 2 (
con − x p < x < 0
p
p
εs $ 2
2 '
+
V x =*
ND # 1 2 NA
NA 2 &
+
−q
x
−
x
⋅
x
−
x ( con 0 < x < xn
%
+
ε s %$ 2
ND p
2N D p ('
,
()
quindi Vbi = ΔV = V (xn ) −V (−x p ) = V (xn ) poiché abbiamo imposto V (−x p ) = 0
V
=V (xn ) = q
bi
%
ND " 1 2 NA
N
x p xn + A x 2p ''
$$ − xn +
εs # 2
ND
2N D &
N A x p = N D xn ⇒ xn =
NA
x
ND p
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-5
2
N D " 1 N A2 2 N 2A 2 N A 2 % qx p N A " N A %
$−
Vbi = q
x +
x +
x '=
+1'
$
ε s $# 2 N D2 p N 2D p 2N D p '&
2ε s $# N D '&
xp =
2ε s
2ε s
ND
NA
Vbi ed allo stesso modo si calcola xn =
V
q NA NA + ND
q N D N A + N D bi
(
(
)
)
con passaggi matematici si arriva a
W = xn + x p =
2ε s ! N A + N D $
#
&V
q #" N A N D &% bi
(III.6)
Se la giunzione è brusca ed asimmetrica (cioè la concentrazione del drogaggio delle due regioni è
molto diverso) la regione di carica spaziale si estende di più nel materiale meno drogato (ad es. per
drogaggio p+-n, cioè drogaggio p molto elevato, W ≅ xn =
qN BW
2ε sVbi
e εm =
, dove NB coincide
εs
qN B
con la concentrazione del materiale meno drogato).
Esempio: Calcolare il potenziale di built-in, l’estensione della regione di carica spaziale e il campo
elettrico massimo di una giunzione p-n con NA=1019 cm-3 e ND=1016 cm-3 a temperatura
ambiente
NA
ND
1016
1016
5x1015
1016
1017
9,09x1015
1016
1018
9,9x1015
1016
1019
9,99x1015
Neq =
1
⎛ N A + ND ⎞
⎜
⎟
⎝ N A ND ⎠
⎛ 1019 ×1016 ⎞
Vbi = 0.0259ln ⎜
= 0.874V
10 2 ⎟
⎝ (1.45 ×10 ) ⎠
W ≅ xn =
Σm =
2ε sVbi
= 3.37 ×10−5 cm = 0.337 µ m
qN D
qN BW
εs
= 5.4 ×104 V / cm
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-6
III.2 Polarizzazione di una giunzione
Applicando una polarizzazione mi discosto dalla condizione di equilibrio termodinamico e il livello di
Fermi non è più costante su tutta la giunzione.
L’applicazione della polarizzazione diretta riduce l’altezza della barriera di una quantità pari alla
polarizzazione applicata e riduce inoltre l’estensione della regione di carica spaziale, mentre
l’applicazione di una polarizzazione inversa ha l’effetto opposto.
L’estensione della regione di carica spaziale assume il seguente valore:
W=
2ε s ⎛ N A + N D
⎜
q ⎝ N AND
⎞
2ε s
⎟ (Vbi − Va ) =
q
⎠
⎛ 1
1 ⎞
+
⎜
⎟ (Vbi − Va )
N
N
D ⎠
⎝ A
che assume il valore per giunzioni asimmetriche
W≅
2ε s (Vbi − Va )
qN B
dove Va è la tensione di polarizzazione applicata (positiva per polarizzazione diretta).
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-7
Quando la giunzione è polarizzata inversamente la regione di carica spaziale varia come la radice
quadrata della tensione applicata.
Il campo elettrico massimo per una giunzione brusca polarizzata si ricava da:
1
ε W = (Vbi − Va )
2 m
⇒
Dispositivi Elettronici – Capitolo III: La giunzione p-n
ε
m
=
2(Vbi − Va )
W
III-8
III.3 Giunzione graduale
Nelle giunzioni graduali la giunzione non è brusca (non si ha drogaggio uniforme nelle regioni n e
p).
Consideriamo dapprima il caso di equilibrio termodinamico.
La distribuzione delle impurezze per una giunzione graduale in modo lineare è illustrato in figura a).
L’equazione di Poisson in questo caso è:
ρ
d 2ψ
dε
q
=−
= − s = − ax
2
dx
εs
εs
dx
−
W
W
≤x≤
2
2
dove a è il gradiente di impurezze. Integrando questa espressione sapendo che
ε =0
in ± W / 2 si
ottiene un andamento del campo elettrico che va come x 2 (fig. b)
ε ( x) = ∫
x
qa
−W /2
εs
x
τ dτ =
qa ⎡τ 2 ⎤
ε s ⎢⎣ 2 ⎥⎦ −W /2
⎡⎛ W
⎢
qa ⎜ 2
= − ⎢⎝
εs ⎢
⎢
⎣
2
⎤
⎞
2
⎟ −x ⎥
⎠
⎥
⎥
2
⎥
⎦
e il campo massimo a x=0 è
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-9
ε
m
=−
qaW 2
8ε s
integrando ancora l’equazione di Poisson si ottiene la distribuzione del potenziale e il diagramma a
bande in figura.
Il potenziale intrinseco della giunzione (o di built-in)
qaW 3
Vbi =
12ε s
E l’estensione della regione di carica spaziale
⎛ 12ε sVbi ⎞
W =⎜
⎟
⎝ qa ⎠
1
3
Il valore della concentrazione delle impurezze ai bordi della regione svuotata (in –W/2 e +W/2) si può
calcolare sapendo che ha un andamento lineare con pendenza a. Considerando che ai bordi della
regione vale la legge di azione di massa, si può calcolare dunque il potenziale di built anche come
segue:
Vbi =
N N
kT
kT " (aW / 2)(aW / 2) % 2kT " aW %
⋅ ln A 2 D =
ln $
ln $
'=
'
q
q $#
q
ni
ni2
'&
# 2ni &
Quando si applica una polarizzazione positiva o negativa la variazione della larghezza della regione
svuotata o di carica spaziale e i diagrammi a bande di energia sono molto simili al caso della
giunzione brusca. Tuttavia la larghezza della regione svuotata varia come (Vbi − Va )1/ 3
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-10
II.1 Capacità della regione svuotata della giunzione
In una giunzione p-n la regione di carica spaziale si comporta come il dielettrico di un condensatore le
cui armature sono le regioni quasi neutre, cioè le zone lontano dalla giunzione dove il potenziale è
costante.
Per calcolare la capacità di piccolo segnale in una giunzione p-n, sostituisco l’espressione per la carica
spaziale Qs di ciascuna regione n e p.
Qs = qN D xn = qN A x p
La capacità per unità di area risulta pari alla derivata della carica al variare della tensione applicata:
C=
dx p
dQs
dx
= qN D n = qN A
dVa
dVa
dVa
poiché x p N A = xn N D
⇒
xp =
xn N D
NA
e
⎛ N ⎞
2ε s
W = xn + x p = xn ⎜1 + D ⎟ =
q
⎝ NA ⎠
dxn
1
=
dVa N D
⎛ 1
1 ⎞
+
⎜
⎟ (Vbi − Va )
⎝ N A ND ⎠
εs
⎛ 1
1 ⎞
2q ⎜
+
⎟ (Vbi − Va )
⎝ N A ND ⎠
da cui è possibile ricavare la capacità per unità di area
C = qN D
dxn
=
dVa
qε s
⎛ 1
1 ⎞
2⎜
+
⎟ (Vbi − Va )
⎝ N A ND ⎠
che è la stessa espressione che si ricava se Va > Vbi dalle espressione
C=
εs
W
[ F / cm 2 ] ricordando che W =
2ε s ⎛ 1
1
+
⎜
q ⎝ N A ND
⎞
⎟ (Vbi − Va )
⎠
III.3.1 Misura della capacità, della Vbi e del drogaggio
Se misuro la capacità al variare della tensione applicata è rappresento graficamente 1/C2 in funzione
del campo applicato
1 2(Vbi − Va ) ⎛ 1
1 ⎞ 2(Vbi − Va ) 1
=
+
⎜
⎟=
C2
qε s
qε s
NB
⎝ N A ND ⎠
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-11
⎛ 1
1 ⎞
si ha una retta la cui pendenza permette di calcolare N B o ⎜
+
⎟ . L’intercetta della retta
⎝ N A ND ⎠
sull’asse delle ascisse invece permette di calcolare il potenziale di built-in Vbi.
Le precedenti relazioni valgono per giunzioni brusche. Nel caso di giunzioni graduali con drogaggio
linearmente variabile si ha:
⎡ qaε s 2 ⎤
Cj =
=⎢
⎥
W ⎣12(Vbi − Va ) ⎦
εs
1
3
In questo caso per ottenere il gradiente del drogaggio e il potenziale intrinseco è necessario riportare
graficamente il valore di 1/C3 in funzione della tensione.
III.3.1 Il Diodo Varactor(Variable Reactor)
Una giunzione polarizzata inversamente può essere utilizzata coma capacità variabile.
Come già visto in precedenza
C j ∝ (Vbi + VR ) − n
o
C j ∝ (VR ) − n
per VR >> Vbi
dove n=1/3 per giunzioni linearmente graduali o ½ per giunzioni brusche. Quindi la sensitività di una
giunzione brusca è superiore.
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-12
Caratteristica corrente-tensione (I-V) nella giunzione p-n
La caratteristica corrente-tensione di una giunzione p-n coincide con la caratteristica del diodo
illustrata in figura.
Diversi meccanismo contribuiscono a formare tale caratteristica:
•
Corrente del diodo ideale: è l’andamento esponenziale in polarizzazione diretta dovuto alla
diffusione dei minoritari in eccesso
•
Corrente per alti livelli di iniezione: Effetto resistenza serie in forte polarizzazione diretta
•
Corrente di ricombinazione: domina per bassissimo livelli di polarizzazione diretta
•
Corrente di generazione: domina per bassi livelli di polarizzazione inversa
•
Corrente di breakdown: è la forte corrente che si osserva per polarizzazione inversa intensa in
corrispondenza della rottura della giunzione
La corrente del diodo ideale
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-13
La caratteristica corrente tensione si ottiene studiando il flusso dei portatori e la loro generazione o
ricombinazione nelle diverse regioni della giunzione, ovvero nella regione di carica spaziale o nelle
regioni quasi neutre.
Per ricavare il flussi di corrente in funzione della tensione applicata si utilizzano:
•
l’equazione di continuità
•
il concetto di tempo di vita dei portatori in eccesso
Come abbiamo visto l’equazione di continuità permette di calcolare la concentrazione dei portatori in
funzione della posizione e del tempo.
Abbiamo anche visto che il flusso di corrente è dovuto alla somma di un contributo di corrente di
deriva dovuto al campo elettrico e un contributo di corrente di diffusione. Ovvero valgono le relazioni
Jn = Jn
deriva
Jp = Jp
+ Jn
deriva
diffusione
+Jp
diffusione
dn
dx
dp
= qµ p pε − qD p
dx
= qµ n nε + qDn
Se considero una giunzione p-n polarizzata direttamente tensione applicata Va solo sulla giunzione
(trascuro la Rserie dei contatti e delle regioni quasi neutre)
Vgiunzione = Vbi − Va , quindi come abbiamo visto avrò una riduzione di barriera per i maggioritari, cioè le
lacune potranno in maggior numero spostarsi da p a n e gli elettroni da n a p. Dopo il passaggio
attraverso la regione i carica spaziale i portatori divengono minoritari e diffondono verso le rispettive
regioni quasi-neutre. Qui in buona parte vengono neutralizzati dai maggioritari iniettati ai contatti.
Quando invece è applicata una polarizzazione inversa Va < 0 la barriera aumenta e il campo elettrico
della regione di carica spaziale tende a spazzare via i portatori minoritari.
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-14
Quindi sia per polarizzazione diretta che inversa, sono le densità di portatori minoritari che
determinano le correnti di una giunzione p-n.
Condizioni al contorno per le densità dei portatori minoritari in funzione di Va
Supponiamo di polarizzare una giunzione p-n e che siano valide le seguenti ipotesi:
•
la regione di carica spaziale è brusca ed al di fuori il campo è nullo
•
Va piccola per non perturbare troppo le popolazioni di portatori e iniezione di basso livello
( Va << Vbi )
•
Trascuro la generazione e ricombinazione nella regione svuotata
•
Inoltre le concentrazioni dei portatori ai capi della regione svuotata dipendono dalla differenza
di potenziale tra questi due punti (secondo la relazione
n2
=e
n1
q (φ2 −φ1 )
kT
).
Se sono vere queste ipotesi allora la concentrazione di portatori al limite della regione di carica
spaziale è N D in prossimità di xn e N A in prossimità di x p .
Quindi all’equilibrio termodinamico
n p0 (− x p ) = nn0 ( xn )e
−
pn0 ( xn ) = p p0 (− x p )e
qVbi
kT
= N D ( xn )e
−
qVbi
kT
−
q (Vbi −Va )
kT
−
q (Vbi −Va )
kT
−
qVbi
kT
= N A ( − x p )e
−
qVbi
kT
mentre se applico Va
n p (− x p ) = N D ( xn )e
pn ( xn ) = N A (− x p )e
Combinando le 4 equazioni ottengo la concentrazione n ' = n − n0 e p ' = p − p0 dei minoritari in
eccesso ai bordi della regione di carica spaziale rispetto all’equilibrio termodinamico:
a
⎡ qV
⎤
kT
n ' p (− x p ) = n p0 (− x p ) ⎢e − 1⎥
⎣
⎦
a
⎡ qV
⎤
kT
p 'n ( xn ) = pn0 ( xn ) ⎢e − 1⎥
⎣
⎦
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-15
cioè la concentrazione dei minoritari è funzione esponenziale della tensione applicata
( pn e n p ≈ f (eVa ) ), mentre la concentrazione dei maggioritari è indipendente da Va .
Vediamo ora le soluzioni dell’equazione di continuità nelle regioni quasi-neutre. Si consideri
l’iniezione di lacune in eccesso al bordo della regione di carica spaziale dalla zona n.
L’equazione di continuità per le lacune minoritarie in eccesso diviene
(
)
pn − pn0
∂pn
∂ 2 pn ( x)
∂ 2 pn ( x)
≅ Dp
−
=
D
+ (G pn − Rpn )
p
∂t
∂x 2
τp
∂x 2
per drogaggio costante ed in regime stazionario (
d 2 p 'n ( x) p 'n ( x)
∂pn
−
= 0 che è una
= 0 ) vale D p
dx 2
τp
∂t
semplice equazione differenziale la cui soluzione è della forma
p 'n ( x) = Ae
−
x − xn
D pτ p
x − xn
+ Be
D pτ p
dove A e B sono costanti determinate dalle condizioni al contorno, mentre
Dpτ p = Lp è la lunghezza
di diffusione delle lacune, cioè la distanza che le lacune riescono a percorrere prima di ricombinare
con un elettrone.
Data la struttura della giunzione illustrata nella figura precedente, considero ora due casi:
1. DIODO a BASE LUNGA ( L p << WB )
2. DIODO a BASE CORTA ( L p >> WB )
Diodo a base lunga
Nel caso di diodo a base lunga vale L p << WB , cioè tutte le lacune ricombinano prima di arrivare al
contatto
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-16
Il profilo dei portatori è esponenziale decrescente con x , quindi il coefficiente B è nullo, e
a
⎡ qV
⎤
kT
− 1⎥ ricavo la condizione al contorno e A. Il profilo dei
dall’equazione p 'n ( xn ) = pn0 ( xn ) ⎢e
⎣
⎦
portatori minoritari in eccesso allora si può scrivere
a
⎡ qV
⎤ −
kT
p 'n ( x) = pn0 ⎢e − 1⎥ e
⎣
⎦
( x − xn )
Lp
Quindi avendo una concentrazione di portatori variabile si genera una corrente di diffusione nelle
regioni quasi-neutre (dove il campo elettrico è praticamente nullo)
a
pn0 ⎡ qV
⎤ −
dpn
kT
J p ( x) = −qDp
= qDp
e
−
1
⎢
⎥e
dx
Lp ⎣
⎦
( x − xn )
Lp
ni 2
= qDp
N D Lp
a
⎡ qV
⎤ −
kT
e
−
1
⎢
⎥e
⎣
⎦
( x − xn )
Lp
Questa corrente di lacune è massima per x = xn e decresce allontanandosi dalla giunzione poiché il
gradiente di lacune decresce. Ma in regime stazionario la corrente totale deve essere costante, allora la
diminuzione della corrente di lacune dal bordo della regione i carica spaziale verso la regione quasi
neutra è compensata dall’aumento del flusso di elettroni iniettato in direzione opposta dal contatto. In
WB la corrente è solo elettronica (quelli iniettati dal contatto) mentre in xn la corrente è solo di lacune.
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-17
Allo stesso modo nella regione drogata p il flusso di elettroni minoritari in eccesso è:
% ( x+x p )
a
ni2 " qV
$e kT −1' e Ln
J n (x) = qDn
N A Ln $#
'&
quindi la corrente totale che è la somma delle due correnti di minoritari è
qV
a
⎛ Dp
⎡ qV
⎤
Dn ⎞ ⎡ kTa ⎤
kT
JTOT ( x) = J p ( xn ) + J n (− x p ) = qni ⎜
+
e
−
1
=
J
e
−
1
⎟
⎥
⎥
0⎢
⎜ N D Lp N A Ln ⎟ ⎢
⎣
⎦
⎣
⎦
⎝
⎠
2
che è chiamata equazione del diodo ideale.
kT
.
q
J 0 è la corrente di saturazione che scorre applicando una tensione Va < 0 dell’ampiezza di alcuni
Diodo a base corta
In questo caso vale L p >> WB e Ln >> WE e la ricombinazione nelle regioni quasi neutre è piccola.
Molti portatori minoritari iniettati riescono cioè a raggiungere il contatto prima di ricombinare.
In questo caso le soluzioni si ottengono approssimando gli esponenziali della relazione
p 'n ( x) = Ae
−
x − xn
D pτ p
x − xn
+ Be
D pτ p
con i primi due termini dello sviluppo in serie di Taylor:
p 'n ( x) = A '+ B '
( x − xn )
Lp
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-18
Il contatto metallico in
x = WB impone che p 'n (WB ) = 0
e valgono ancora le condizioni al
contorno
a
⎡ qV
⎤
kT
n ' p (− x p ) = n p0 (− x p ) ⎢e − 1⎥
⎣
⎦
a
⎡ qV
⎤
kT
p 'n ( xn ) = pn0 ( xn ) ⎢e − 1⎥
⎣
⎦
quindi la soluzione per le lacune in eccesso nella zona n diviene
a
⎛ qV
⎞ ⎛ ( x − xn ) ⎞
kT
p 'n ( x) = pn0 ⎜ e − 1⎟ ⎜1 −
⎟
W
'
B
⎠
⎝
⎠⎝
dove
W 'B = WB − xn
è la lunghezza della regione quasi neutra di tipo n. Quindi la concentrazione
delle lacune decresce linearmente
L’approssimazione L p >> WB equivale a dire che quasi tutte le lacune diffondono attraverso la regione
n prima di ricombinarsi, cioè il loro tempo di vita tende ad infinito ( τ p → ∞ ).
Essendo la variazione di concentrazione lineare, la corrente di diffusione (pari alla derivata della
concentrazione) delle lacune è costante.
pn0
dpn
J p ( x) = −qDp
= qDp
dx
W 'B
2
a
⎡ qV
⎤
n
i
kT
⎢e − 1⎥ = qDp
N DW 'B
⎣
⎦
a
⎡ qV
⎤
kT
e
−
1
⎢
⎥
⎣
⎦
che è un’espressione simile alla precedente. Cambia solo la lunghezza caratteristica:
•
Nel diodo a base lunga la lunghezza caratteristica coincide con la lunghezza di diffusione dei
portatori minoritari
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-19
•
Nel diodo a base corta la lunghezza caratteristica coincide con la lunghezza della regione
quasi neutra
La corrente totale è dunque
qV
a
⎡ qV
⎤
⎛ Dp
Dn ⎞ ⎡ kTa ⎤
kT
JTOT ( x) = J p ( xn ) + J n (− x p ) = qni ⎜
+
e
−
1
=
J
e
−
1
⎥
⎥
⎟⎢
0 ⎢
N
W
'
N
W
'
A
E ⎠⎣
⎝ D B
⎦
⎣
⎦
2
Nel caso reale in genere ho una parte della giunzione a base lunga mentre l’altra è a base corta. In
questo caso nella corrente totale ho contributi misti.
J 0 è in genere dominata dalla regione meno drogata.
Correnti di generazione/ricombinazione nella regione di carica spaziale e per alti livelli di iniezione
Le correnti del diodo trovate vertevano su eventi nelle regioni quasi-neutre.
Nella regione di carica spaziale invece si concentrano i fenomeni di generazione e ricombinazione.
Tale regione ha un’estensione tipica dell’ordine di 10-4 cm.
Se utilizzo la teoria Shockley-Hall-Read e considero
U =−
dn dp
=
=
dt dt
2
ni (e
qVa
kT
⎡
pn = ni 2 e
q (φ p −φn )
kT
qVa
2 kT
= ni e
− 1)
⎛ Ei − Et ⎞ ⎤
⎟⎥
⎝ kT ⎠ ⎦
τ 0 ⎢ p + n + 2ni cosh ⎜
⎣
In polarizzazione diretta Va > 0 e risulta U > 0 e come abbiamo già visto corrisponde ad un fenomeno
in cui domina la RICOMBINAZIONE.
In polarizzazione inversa Va < 0 e risulta U < 0 che corrisponde ad un fenomeno in cui domina la
GENERAZIONE.
La corrente di generazione/ricombinazione è pari all’integrale in tutta la regione di carica spaziale di
U:
Jr = q
xn
∫ Udx
− xp
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-20
E’ un integrale di difficile soluzione, del quale si cerca una soluzione qualitativa assumendo che la
funzione U sia massima a centro banda dove Et = Ei .
Si dimostra che U è massima quando (p+n) al denominatore di U è minimo e, se
quando
p = n = ni e
qVa
2 kT
pn = ni e
2
qVa
kT
,
.
Se tali ipotesi sono valide, cioè se l’integrale è dominato dalla regione dove U è massimo (cioè in una
porzione x’ della regione di carica spaziale) si può scrivere
2
qx ' ni (e
Jr =
2ni (e
τ0 =
1
N tσ vth
Quindi
qVa
2 kT
qVa
kT
− 1)
+ 1)τ 0
qV
qx ' ni 2 kTa
≈
e
2τ 0
è sempre il tempo di vita associato alla ricombinazione dei portatori in eccesso.
Jr ≈ e
qVa
2 kT
E’ importante notare il “2” al denominatore dell’esponente.
Se si assume x ' = W il rapporto tra la corrente totale è quella di ricombinazione diventa:
L p 2qVkTa
J TOT 2ni Ln
=
(
+
)e
Jr
W N A ND
cioè al crescere di Va la corrente di ricombinazione diviene meno importante.
La corrente in polarizzazione diretta si può dunque esprimere in modo generale come
JF ≈ e
qVa
η kT
dove η è chiamato fattore di idealità.
•
Quando domina la corrente di diffusione η ≈ 1 (alti livelli di iniezione)
•
Quando domina la corrente di ricombinazione η ≈ 2 (bassi livelli di iniezione)
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-21
Inoltre per alti livelli di iniezione la caduta di potenziale non avviene solo in prossimità della
giunzione ma anche sulle regioni quasi-neutre. Si ha l’effetto resistenza serie
I F = I 0e
q (Va − IR )
kT
=
I 0e
e
qVa
kT
q ( IR )
kT
Il termine al denominatore nel membro di destra dipende da R che è la resistenza serie del dispositivo
ed è un fattore di riduzione della corrente di polarizzazione diretta
In polarizzazione inversa la corrente di generazione nella regione di carica spaziale sempre con le
assunzioni precedenti è
Jg =
qni xi
2τ 0
dove xi è la frazione di W dove ho massima velocità di generazione. Se N D << N A :
W=
2ε s
2ε s kT
N D N A qVa
(Vbi − Va ) =
(ln
−
)
qN D
q2 ND
ni 2
kT
e
1/2
! 2ε kT $
xi = ## 2 s &&
" q ND %
(
qV
N
N +
* ln D − a − ln D ni -,
ni2 kT
*)
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-22
Per Va grande xi → W
In un diodo a base lunga vale
JTOT 2ni ⎡ Ln Lp ⎤
=
+
⎢
⎥
Jg
xi ⎣ N A N D ⎦
In polarizzazione inversa il contributo dominante viene dalla corrente generata nella regione di carica
spaziale e il rapporto
J TOT
è molto inferiore a 1, tuttavia la corrente inversa si compone di due
Jg
contributi:
J R = J0 + J g
dove J 0 è la corrente di saturazione che domina in materiali quali il silicio ed il germanio, mentre nel
GaAs diviene molto importante il termine di generazione.
III.4 Corrente di rottura della giunzione
Come si è visto, all’aumentare della polarizzazione inversa aumentano sia la regione di carica spaziale
W che il campo elettrico massimo
ε
m
. Ad un certo valore di potenziale applicato tuttavia si manifesta
la rottura della giunzione (breakdown) e le correnti aumentano improvvisamente. Le rotture possono
essere di due tipi:
•
Controllate: ad es. la rottura zener o quella a valanga che sono processi reversibili
•
Irreversibili: si ha la fusione di una regione della giunzione che diviene irrimediabilmente
rovinata.
La tensione a cui avviene il breakdown della giunzione dipende:
•
Dal materiale semiconduttore
•
Dal suo drogaggio p ed n
•
Dalla struttura della giunzione
III.4.1 Rotture reversibili
Per campi elettrici elevati esistono due tipi di breakdown a zener e a valanga.
III.4.1.1 Rottura a valanga
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-23
Si consideri un elettrone in movimento nella regione di carica spaziale di una giunzione p-n
polarizzata inversamente. L’elettrone percorre in media una distanza l (libero cammino medio) prima
di una collisione con il reticolo che gli fa perdere energia.
Tra due collisioni l’elettrone acquisisce un’energia dal campo elettrico pari a
l
ΔE = q ∫ ε dx
o
il termine sotto integrale corrisponde al prodotto scalare di vettori.
Se l’energia acquisita è sufficiente l’elettrone è in grado di rompere un legame creando così una
coppia elettrone-lacuna.
Da lì in poi vi sono tre portatori. Nell’ipotesi che abbiano uguale massa, per il principio di
conservazione dell’energia e della quantità di moto per rompere il legame occorre che l’elettrone
abbia energia cinetica pari a
Ecin =
3
Eg
2
In polarizzazione inversa gli elettroni arrivano nella regione di carica spaziale dalla zona p (trascuro le
lacune che arrivano da n). Ai bordi della regione di carica spaziale (tra xp e xa e tra xc e xn) il campo
elettrico è piccolo e gli elettroni hanno poca energia e non riescono a generare per impatto nuovi
portatori.
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-24
L’effetto valanga è concentrato al centro della regione di carica spaziale entro un Δx
Sia n0 la densità di elettroni entranti, la densità di elettroni aumenta in x per effetto valanga tra xa e x,
cosicché in dx entrano (n0+n1) elettroni.
La probabilità che gli elettroni in dx creino un numero di coppie è pari a α n dx , dove α n è il
coefficiente di ionizzazione da impatto che è funzione del campo elettrico.
L’aumento della concentrazione di elettroni (e quindi di lacune) generato in dx dagli elettroni entranti
è allora
dn' = dp = α n ⋅ n ⋅ dx = α n (n0 + n1 )dx
Supponendo che da destra di xc non entrino lacune, ogni lacuna entrante in x si è formata tra x e xc
Chiamo tale concentrazione p2. Anche queste lacune realizzano effetto valanga e creano coppie
elettrone-lacuna generando una variazione di concentrazione di elettroni
dn'' = dp = α p ⋅ p ⋅ dx = α p ( p2 )dx
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-25
L’aumento totale è allora
dn' + dn'' = dn = α n (n0 + n1 )dx + α p ⋅ p2 ⋅ dx
e la densità di elettroni che arriva in xc
n f = n0 + n1 + n2
(n2 = p2 )
dalle due relazioni precedenti
dn
= (α n − α p )(n0 + n1 ) + α p n f
dx
se pongo per definizione α n = α p = α e integro la precedente relazione con
n( xa ) = n0 , n( xc ) = n f ottengo la concentrazione degli elettroni creati in Δx
n f − n0 = n f
xc
∫ α dx
xa
Si definisce
M=
nf
n0
1
=
xc
1 − ∫ α dx
xa
xc
La rottura a valanga si verifica quando
∫ α dx = 1 cioè per M → ∞
xa
Il coefficiente di ionizzazione α dipende dal campo elettrico e la sua dipendenza può essere calcolata.
Se
n*
è la concentrazione di elettroni che arrivano in x con energia sufficiente a creare coppie:
n = n⋅e
*
−
d
l
dove n è la densità totale di elettroni, l è il libero cammino medio, ed il termine
e
−
d
l
è la probabilità
che un elettrone non abbia subito collisioni per una distanza d sufficiente ad acquisire l’energia
sufficiente alla ionizzazione E1.
Se
ε è il campo elettrico medio, allora d =
E1
(E/q è un potenziale e il campo elettrico è perciò
qε
E
dx
). Il numero di collisioni ionizzanti è inoltre proporzionale a
.
d
qd
Se l’elettrone ha energia maggiore o pari a E1
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-26
− 1
dx
' qε
dn = A n
=A
e lqε ⋅ n ⋅ dx
d
E1
E
' *
ma avevamo visto che
dn' = α n ⋅ n ⋅ dx per cui si può ricavare la dipendenza di α dal campo
elettrico
B
α = Aε e ε
−
In prossimità della rottura si ha un aumento del campo elettrico ed un brusco aumento di corrente. Se
si tiene conto che l’ipotesi di regione di carica spaziale costante in realtà non è valida ma aumenta con
la polarizzazione inversa applicata occorre modificare il fattore M che diviene:
M=
1
⎛V ⎞
1− ⎜ R ⎟
⎝ BV ⎠
n
,
2<n<6
dove VR è la tensione inversa applicata e BV è la tensione di breakdown, il cui valore tipico è
compreso tra -5V e -100V.
Per porre in relazione la tensione di breakdown con i parametri del materiale si consideri una
giunzione asimmetrica con ad esempio N A << N D e si supponga che la rottura avvenga quando il
campo elettrico massimo raggiunge un valore critico
ε
xc
che faccia tendere all’unità
CRITICO
∫ α dx = 1.
xa
Abbiamo visto che il campo elettrico massimo risulta
ε
m
≅
2qN A VR
εs
con ( VR >> Vbi ) e si può
ricavare la tensione di rottura che è ottenuta sostituendo il campo elettrico con
inversa con quella di breakdown. Per cui BV =
ε
CRITICO
e la tensione
ε sε 2CRITICO
2qN A
II.4.1.2 Rottura ZENER
Anche la rottura ZENER della giunzione è una rottura di tipo reversibile. La giunzione in questo caso
è costituita di materiali pesantemente drogati detti degeneri (i livelli di Fermi possono penetrare nelle
rispettive bande). All’aumentare del drogaggio della giunzione p-n la regione di carica spaziale si
riduce e la rottura zener diviene più probabile.
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-27
Infatti, come illustrato in figura quando si polarizza inversamente tale giunzione si riesce ad allineare
la banda di conduzione della regione drogata n con quella di valenza della zona p. Se la distanza a pari
energia tra le due bande è piccola, viene strappato un elettrone dal suo legame in banda di valenza e
spostato per effetto tunnel in quella di conduzione mantenendone l’energia.
L’effetto tunnel è un fenomeno probabilistico e non deterministico. Per valutarne la probabilità
approssimo la barriera vista dagli elettroni con un triangolo
L’energia della barriera EB varia linearmente tra la banda proibita di energia E g e 0 e il campo elettrico
medio è
E
dove L è la distanza tra le due bande.
ε = qL
g
La probabilità di passaggio θ è funzione di EB
L
θ ≈e
−2
∫
0
2 m* EB
h2
dx
risolvendo l’integrale si ottiene
−
B
θ =e ε =e
−
qBL
Eg
,
dove
4 2m* 3/ 2
B=
Eg
3qh
quindi la probabilità di passaggio diminuisce esponenzialmente al diminuire del campo elettrico o
all’aumentare di L.
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-28
La corrente di tunnelling è pari al prodotto
I tunn = AqNV θ
(Area) × (carica elettronica) × (n.elettroni in BV nella regione p che corrispondono a stati vuoti in BC
di pari energia) × probabilità di attraversamento della barriera
NV è il prodotto della densità N di elettroni per la loro velocità.
Esempio: Calcolare la corrente di tunnelling in una giunzione p-n di area A=10-5 cm2, sapendo che la
distanza L tra le bande è 4nm, che Eg ≈ 1eV e che il campo elettrico è di 106 V/cm.
Posso calcolare la probabilità di tunnelling attraverso la formula θ = e
−
qBL
Eg
ottenendo
θ ≈ 10−7 . Inoltre calcolo NV = N ⋅ vth sapendo che la densità N di elettroni che vedono stati
vuoti in BC è praticamente la densità atomica cioè 1022 cm-3, e vth = 107 cm / s .
Quindi 1029 elettroni al secondo per unità di area colpiscono la barriera e risulta
I tunn = AqNV θ = 10−5 ⋅1.62 ×10−19 ⋅1029 ⋅10−7 = 1.62 ×10−2 A = 16.2mA
Tipicamente la tensione di breakdown di una rottura zener è inferiore a 5 V ed è inferiore di quella a
valanga, ma in certi casi i due processi coesistono e le tensioni di rottura quasi coincidono.
Effetto della temperatura
In polarizzazione diretta vale
I Diffusione
I Ricombinazione
≈e
−
( Eg − qVa )
2 kT
quindi all’aumentare della temperatura il rapporto aumenta è la curva diviene sempre più vicina a
quella ideale (η ≅ 1)
In polarizzazione inversa la corrente di saturazione inversa è proporzionale a
calcolare E g dal grafico J 0 vs
J0 ∝ e
−
Eg
kT
( si può
1
) e quindi all’aumentare della temperatura il rapporto aumenta e la
T
corrente di saturazione domina quella di generazione.
Per una giunzione asimmetrica p+-n vale
I Diffusione
I Generazione
=
ni L p τ g
N DW τ p
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-29
che è proporzionale a ni . Questa relazione conferma che all’aumentare della temperatura la corrente
di diffusione diviene dominante.
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-30
Circuiti equivalenti in statica e per piccolo segnale
Le quattro configurazioni principali sono illustrate in figura.
Il caso (a) rappresenta il diodo ideale ed è un circuito aperto per VD < 0 ed un corto circuito per
I D > 0.
Il caso (b) tiene conto della tensione di soglia Vγ quando il diodo è polarizzato direttamente.
Il caso (c) tiene conto della resistenza del dispositivo quando questo è polarizzato direttamente.
In fine il caso (d) tiene conto sia di Ron che della tensione di soglia Vγ .
Spetta al progettista decidere di caso in caso quale modello utilizzare. E’ possibile anche considerare
nel caso di polarizzazione inversa una Resistenza molto grande Roff al posto del circuito aperto.
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-31
Modello per piccolo segnale e bassa frequenza
Calcolato il punto di lavoro si può verificare qual’è il comportamento del dispositivo per piccole
variazioni attorno a questo punto. Tali variazioni possono essere lente (bassa frequenza) o molto
veloci (alta frequenza).
Nell’intorno del punto di lavoro la risposta del diodo è stata approssimata con una retta.
In assenza di segnale la corrente nel diodo risulta dalla relazione
I D = Ioe
VD
VT
. Quando viene
sovrapposto il segnale vd , la tensione istantanea del diodo diviene vD (t ) = VD + vd (t ) , quindi la
corrente istantanea iD = I o e
iD = I o e
(VD + vd )
VT
vD
VT
che si può riscrivere come
VD
VT
= Ioe e
vd
VT
= I De
vd
VT
.
Se il segnale è piccolo posso sviluppare in serie di Taylor l’esponenziale ottenendo
iD ≈ I D (1 +
vd
I
) = I D + D vd che è la somma di una componente continua e di una variabile nel
VT
VT
tempo funzione di vd . Quindi in alternata
id = g D vd
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-32
con g D =
ID
definita conduttanza di piccolo segnale del diodo in [Ω −1 ] e la resistenza di piccolo
VT
segnale è il suo reciproco:
rD =
VT
.
ID
Quindi si procede in due fasi:
•
Si verifica che il diodo sia in conduzione utilizzando i modelli circuitali in continua già visti e
se ne verifica lo stato, trovando il punto di lavoro
•
Si sostituisce al diodo nell’analisi di piccolo segnale un circuito aperto se il diodo è OFF,
altrimenti si sostituisce il diodo con la resistenza rD
Modello per piccolo segnale e alta frequenza
In alta frequenza occorre considerare anche gli effetti capacitivi.
La capacità di svuotamento vista in precedenza domina in una giunzione p-n quando il diodo è
polarizzato inversamente. Quando applico una polarizzazione diretta c’e’ un contributo dovuto alla
ridistribuzione delle cariche immagazzinate nelle regioni neutre che porta alla formazione di una
capacità di diffusione Cd.
La Cd delle lacune immagazzinate nella regione neutra n si ottiene dalla relazione
Cd = A
dove
dQp
dV
Qp = qLp pno (e
qV
kT
− 1) è la carica associata all’iniezione dei minoritari per unità di
area immagazzinata nella regione n (ottenuta integrando le lacune in eccesso nella regione neutra).
Si ottiene quindi
Cd =
Aq 2 L p pno
kT
e
qV
kT
Nel circuito equivalente in polarizzazione diretta vi sono dunque, oltre alla resistenza che tiene conto
della corrente che circola nel diodo, anche due capacità.
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-33
Tale circuito equivalente è una buona approssimazione per piccoli segnali sovrapposti alla
polarizzazione diretta.
In polarizzazione inversa invece il circuito equivalente è costituito dalla sola capacità di svuotamento
(o della giunzione).
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-34
L’eterogiunzione
E’ una giunzione tra due materiali differenti, cioè con bande proibite di energia, affinità elettronica e
funzioni di lavoro differenti.
Si ha discontinuità di banda si in banda di conduzione che in banda di valenza come illustrato in
figura.
Valgono le seguenti relazioni:
ΔEC = q( χ 2 − χ1 )
ΔEV = Eg1 + q χ1 − ( Eg 2 + q χ 2 ) = ΔEg − ΔEC
Nella figura si è assunto che ci sia una concentrazione trascurabile di difetti all’interfaccia.
Ci sono alcune regole generali da rispettare nella costruzione del diagramma a bande:
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-35
•
Il livello di Fermi deve essere costante
•
Il livello del vuoto deve essere continuo
•
L’affinità elettronica deve essere costante nel materiale
Il potenziale intrinseco globale è pari a
Dove
Vbi = Vbi1 + Vbi 2
Vbi1 e Vbi2 sono i potenziali elettrostatici all’equilibrio nei due semiconduttori.
Supponendo che il potenziale e il flusso di portatori liberi siano continui all’interfaccia posso derivare
l’estensione della regione di carica spaziale e della capacità dall’equazione di Poisson con condizione
ε
al contorno che all’interfaccia ε1
1
= ε 2ε 2 .
ε 2 N 2 (Vbi − Va )
ε1 N1 + ε 2 N 2
ε N (V − V )
Vb 2 = 1 1 bi a
ε1 N1 + ε 2 N 2
Vb1 =
e le larghezze di svuotamento sono:
x1 =
2ε1ε 2 N 2 (Vbi − Va )
qN1 (ε1 N1 + ε 2 N 2 )
x2 =
2ε1ε 2 N1 (Vbi − Va )
qN 2 (ε1 N1 + ε 2 N 2 )
Dispositivi Elettronici – Capitolo III: La giunzione p-n
III-36