Modulo di Matematica ed Informatica per il Corso di Laurea in Farmacia
Soluzioni dello scritto del 3 giugno 2014
Esercizio 1.
Indichiamo con xi il numero di battiti cardiaci al minuto, in ordine crescente, e con fi le
frequenze assolute:
x1 = 66,
f1 = 4,
x2 = 67,
f2 = 2,
x3 = 68,
f3 = 5,
x4 = 69,
f4 = 3,
x5 = 70,
f5 = 3,
x6 = 71,
f6 = 1,
x7 = 72,
f7 = 2.
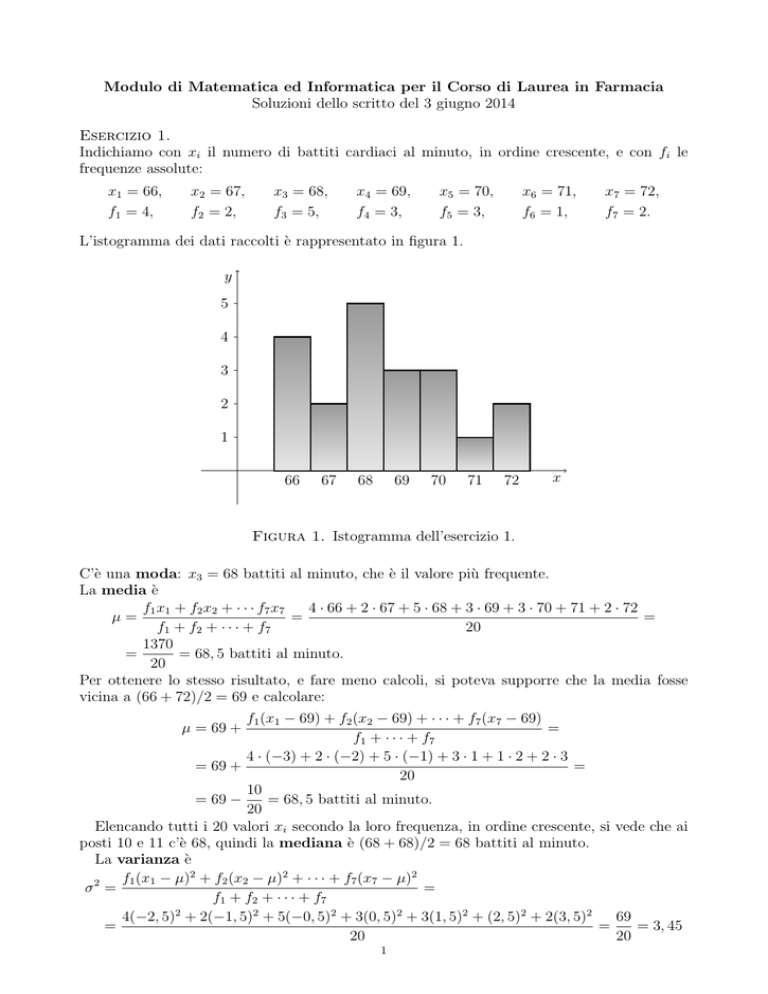
L’istogramma dei dati raccolti è rappresentato in figura 1.
y
5
4
3
2
1
66
67
68
69
70
71
72
x
Figura 1. Istogramma dell’esercizio 1.
C’è una moda: x3 = 68 battiti al minuto, che è il valore più frequente.
La media è
f 1 x1 + f 2 x2 + · · · f 7 x7
4 · 66 + 2 · 67 + 5 · 68 + 3 · 69 + 3 · 70 + 71 + 2 · 72
µ=
=
=
f1 + f2 + · · · + f7
20
1370
=
= 68, 5 battiti al minuto.
20
Per ottenere lo stesso risultato, e fare meno calcoli, si poteva supporre che la media fosse
vicina a (66 + 72)/2 = 69 e calcolare:
f1 (x1 − 69) + f2 (x2 − 69) + · · · + f7 (x7 − 69)
=
f1 + · · · + f7
4 · (−3) + 2 · (−2) + 5 · (−1) + 3 · 1 + 1 · 2 + 2 · 3
= 69 +
=
20
10
= 69 −
= 68, 5 battiti al minuto.
20
Elencando tutti i 20 valori xi secondo la loro frequenza, in ordine crescente, si vede che ai
posti 10 e 11 c’è 68, quindi la mediana è (68 + 68)/2 = 68 battiti al minuto.
La varianza è
f1 (x1 − µ)2 + f2 (x2 − µ)2 + · · · + f7 (x7 − µ)2
σ2 =
=
f1 + f2 + · · · + f7
4(−2, 5)2 + 2(−1, 5)2 + 5(−0, 5)2 + 3(0, 5)2 + 3(1, 5)2 + (2, 5)2 + 2(3, 5)2
69
=
=
= 3, 45
20
20
µ = 69 +
1
√
da cui segue che lo scarto quadratico medio è σ = 3.45 ' 1, 86 battiti al minuto, dove
' significa “circa”.
Riassumendo:
• la media è 68,5 battiti al minuto,
• la mediana è 68 battiti al minuto,
• la moda è 68 battiti al minuto,
• la varianza è 3,45,
• lo scarto quadratico medio è circa 1,86 battiti al minuto.
Esercizio 2.
Indichiamo con
Ω = gli abitanti di Pontegradella con più di 50 anni;
M + = l’evento che un abitante di Pontegradella con più di 50 anni sia malato di diabete;
M − = l’evento che un abitante di Pontegradella con più di 50 anni non sia malato di diabete;
D = l’evento che il medico di Pontegradella diagnostichi il diabete ad un abitante di Pontegradella con più di 50 anni;
N = l’evento che il medico di Pontegradella non diagnostichi il diabete ad un abitante di
Pontegradella con più di 50 anni.
Il testo dell’esercizio ci dice che:
p(M + ) = 15% = 0, 15,
p(D|M + ) = 92% = 0, 92,
p(D|M − ) = 3% = 0, 03.
Al punto (a) l’esercizio ci chiede di calcolare la probabilità condizionata p(M + |D), mentre al
punto (b) ci chiede di calcolare p(M − |N ).
(a) Si noti che p(M − ) = 1 − p(M + ) = 85% = 0, 85. La formula di Bayes, combinata con la
legge delle alternative, ci dice che
p(D|M + ) p(M + )
p(D|M + ) p(M + )
=
=
p(D)
p(D|M + ) p(M + ) + p(D|M − ) p(M − )
0, 92 · 0, 15
0, 138
0, 138
=
=
=
' 0, 8440 = 84, 40%,
0, 92 · 0, 15 + 0, 03 · 0, 85
0, 138 + 0, 0255
0, 1635
p(M + |D) =
dove ' significa “circa” e abbiamo approssimato la percentuale alla seconda cifra decimale.
(b) Al punto (a) abbiamo calcolato che p(D) = 0, 1635, quindi p(N ) = 1 − p(D) = 0, 8365 =
83, 65%. Inoltre dal testo segue che
p(N |M − ) = 1 − p(D|M − ) = 97% = 0, 97.
Possiamo concludere allora applicando ancora la formula di Bayes:
p(M − |N ) =
p(N |M − ) p(M − )
0, 97 · 0, 85
0, 8245
=
=
' 0, 9857 = 98, 57%.
p(N )
0, 8365
0, 8365
Riassumendo:
• la risposta alla domanda (a) è circa 84, 40%,
• la risposta alla domanda (b) è circa 98, 57%.
Esercizio 3.
L’esponenziale è definito per qualsiasi numero reale e la frazione è definita se e solo se il
denominatore è diverso da zero, cioè se e solo se x 6= 0, quindi il dominio della funzione f è
R \ {0} =]−∞, 0[ ∪ ]0, +∞[.
La funzione f non è pari, per esempio perché f (−1) = 2 − e3 6= 2 + e−3 = f (1), né dispari,
ancora perché f (−1) = 2 − e3 6= −2 − e−3 = −f (1).
Studiamo gli eventuali asintoti della funzione f .
2
Avendo escluso 0 dal dominio, calcoliamo
2x + e−3x
0 + e0
1
=
=
= −∞,
x→0
x→0
x
0−
0−
0 + e0
2x + e−3x
1
=
lim+ f (x) = lim+
= + = +∞,
+
x→0
x→0
x
0
0
perciò f ha l’asintoto verticale x = 0 per x che tende a 0.
Riguardo agli altri asintoti, si ha
lim− f (x) = lim−
e−3x
e+∞
2x + e−3x
= lim 2 +
=2+
= −∞,
x→−∞
x→−∞
x→−∞
x
x
−∞
per gerarchie di infinito, perché l’esponenziale va all’infinito più velocemente di una funzione
polinomiale, quindi f non ha asintoto orizzontale sinistro, cioè per x → −∞. Per verificare
se f abbia l’asintoto obliquo calcoliamo
lim f (x) = lim
f (x)
2x + e−3x
2 e−3x
e+∞
= lim
+
= +∞,
=
lim
=
0
+
x→−∞ x
x→−∞
x→−∞ x
x2
x2
+∞
ancora per gerarchie di infinito, perciò f non ha asintoto obliquo per x → −∞.
Per x → +∞, si ha
lim
2x + e−3x
e−3x
e−∞
0+
= lim 2 +
=2+
=2+
= 2,
x→∞
x→∞
x→∞
x
x
∞
∞
quindi f ha l’asintoto orizzontale y = 2 per x → +∞.
Calcoliamo la derivata prima della funzione f . Come abbiamo già osservato prima, si ha
lim f (x) = lim
f (x) = 2 +
e−3x
,
x
quindi
Df (x) = D
Ricordando che un quoziente
g(x)
h(x)
e−3x
x
.
ha derivata
D(g(x)) · h(x) − g(x) · D(h(x))
(h(x))2
e che D(ef (x) ) = ef (x) Df (x), nel nostro caso si ottiene
e−3x (−3)x − e−3x
e−3x (3x + 1)
Df (x) =
=−
.
x2
x2
Ricordando sempre che e−3x > 0 per ogni x ∈ R e che x2 > 0 per ogni x nel dominio, si ha
f 0 (x) > 0 se e solo se 3x + 1 6 0, cioè se e solo se x 6 −1/3, nel dominio.
Ne segue che
• f è crescente per x < −1/3,
• f ha un massimo relativo in x = −1/3, dove f (−1/3) = 2 − 3e ' −6, 15,
• f è decrescente per −1/3 < x < 0,
• f è sempre decrescente per x > 0.
Osserviamo che non ci sono punti di minimo (né relativo né assoluto).
La derivata seconda di f (x) è
(e−3x (−3)(3x + 1) + e−3x 3)x2 − 2xe−3x (3x + 1)
f (x) = −
=
x4
xe−3x (9x2 + 6x + 2)
e−3x (9x2 + 6x + 2)
=
=
.
x4
x3
Siccome 9x2 + 6x + 2 = (3x + 1)2 + 1 ed e−3x sono sempre positivi, si ha f 00 (x) > 0 se e solo
se x3 > 0, nel dominio, che accade se e solo se x > 0. Ne segue che
00
3
• f è concava per x < 0,
• f è convessa per x > 0.
Osserviamo che non ci sono punti di flesso (0 non può essere punto di flesso perché fuori dal
dominio).
Si può allora tracciare un grafico approssimativo della funzione f (x) come nella figura 2.
y
10
5
y=2
2
−1
−0.5
0.5
1
1.5
2
x
(− 31 , 2 − 3e) −5
−10
−15
Figura 2. Grafico della funzione f (x) dell’esercizio 3
Esercizio 4.
Si ha che 1 − e0 = 0 e 1 − cos(0) = 0, quindi il limite dato è una forma indeterminata 00 .
Applicando i teoremi di De L’Hôpital, troviamo
2
2
1 − ex
−2xex
lim
= lim
= −2
x→0 1 − cos(x)
x→0 sen(x)
dove l’ultima uguaglianza segue dal limite fondamentale
x
lim
= 1.
x→0 sen(x)
Equivalentemente, si poteva continuare usando ancora i teoremi di De L’Hôpital:
2
2
2
−2xex
−2ex − 4x2 ex
−2e0 − 0
= lim
= lim
=
= −2
x→0 sen(x)
x→0
cos(x)
1
Esercizio 5.
Il grafico di f (x) mostra che f (x) ha massimo assoluto in x0 = 0, dove f (0) = 2, quindi la
v.a.c. X ha moda x0 = 0. La media di X è
Z +∞
Z 0
Z +∞
Z 0
2x
xf (x) dx =
2xe dx +
0 dx =
2xe2x dx,
−∞
−∞
0
−∞
che possiamo risolvere per parti, secondo la formula
Z
Z
0
g(x)h (x) = g(x)h(x) − g 0 (x)h(x)
4
per opportune funzioni g e h.
Poniamo g(x) = x e h0 (x) = 2e2x , cosı̀ g 0 (x) = 1 e h(x) = e2x , quindi
Z
Z
1
2x
2x
2xe dx = xe − e2x = xe2x − e2x
2
da cui segue che l’integrale generalizzato si può risolvere cosı̀:
0
Z 0
Z 0
1 2x
2x
2x
2x
2xe dx = lim
2xe dx = lim xe − e
=
r→−∞ r
r→−∞
2
−∞
r
1
1 2r
r
1 0
1
2r
= − − lim −2r = −
= lim 0 − e − re + e
r→−∞
2
2
2 r→−∞ e
2
dove nell’ultima uguaglianza abbiamo usato le gerarchie di infinito.
In conclusione, la media della v.a.c. X è −1/2.
Dipartimento di Matematica e Informatica — Università degli Studi di Ferrara
5












